
掌握本课程的基本技能,要熟练掌握并会应用。如行列式的计算、 矩阵的运算、矩阵初等变换和逆矩阵的计算、矩阵及向量组秩的计算、 向量组线性相关性的判别、线性方程组的求解、施密特正交化过程、 矩阵特征值与特征向量的计算、实对称矩阵的正交相似变换、化二次 型为标准形的方法等。 该课程基本要求分两个层次,其中对概念与理论用“理解”和“熟 悉”表述,对方法和运算用“熟练掌握”和“会”表述,后者为较高的要 求。 三、先修课程 《高等数学》 四、课程教学重、难点 第一章n阶行列式 教学重点:n阶行列式的定义、行列式的性质、克莱姆(Gramer)法则。 教学难点:会应用行列式的定义、性质和行列式按行(列)展开的定理 计算行列式:会用克菜姆法则求解符合法则要求的非齐次线性方程组。 第二章矩阵 教学重点:矩阵的线性运算、矩阵乘法运算、矩阵转置运算、方阵的 行列式、方阵的幂以及它们的运算规律:逆矩阵的性质以及方阵可逆 的充分必要条件、伴随矩阵的概念、用伴随矩阵求可逆矩阵的逆矩阵: 矩阵的初等变换、初等矩阵、初等矩阵的性质和矩阵等价。 教学难点:矩阵的秩、用初等行变换求矩阵的秩和矩阵的逆矩阵的方 法、利用秩的性质解决一些问题;分块矩阵的概念及分块矩阵的运算
8 掌握本课程的基本技能,要熟练掌握并会应用。如行列式的计算、 矩阵的运算、矩阵初等变换和逆矩阵的计算、矩阵及向量组秩的计算、 向量组线性相关性的判别、线性方程组的求解、施密特正交化过程、 矩阵特征值与特征向量的计算、实对称矩阵的正交相似变换、化二次 型为标准形的方法等。 该课程基本要求分两个层次,其中对概念与理论用“理解”和“熟 悉”表述,对方法和运算用“熟练掌握”和“会”表述,后者为较高的要 求。 三、先修课程 《高等数学》 四、课程教学重、难点 第一章 n 阶行列式 教学重点:n 阶行列式的定义、行列式的性质、克莱姆(Gramer)法则。 教学难点:会应用行列式的定义、性质和行列式按行(列)展开的定理 计算行列式;会用克莱姆法则求解符合法则要求的非齐次线性方程组。 第二章 矩阵 教学重点:矩阵的线性运算、矩阵乘法运算、矩阵转置运算、方阵的 行列式、方阵的幂以及它们的运算规律;逆矩阵的性质以及方阵可逆 的充分必要条件、伴随矩阵的概念、用伴随矩阵求可逆矩阵的逆矩阵; 矩阵的初等变换、初等矩阵、初等矩阵的性质和矩阵等价。 教学难点:矩阵的秩、用初等行变换求矩阵的秩和矩阵的逆矩阵的方 法、利用秩的性质解决一些问题;分块矩阵的概念及分块矩阵的运算

第四章n维向量 教学重点:维向量的概念、向量的线性运算、向量的线性组合与线 性表示、向量组的线性相关性的概念;向量组线性相关、线性无关的 有关性质及判别法:向量组极大无关组的概念、求向量组极大无关组 的方法;向量组等价、向量组的秩、矩阵的秩与其行(列)向量组的秩 之间的关系、求向量组秩的方法。 教学难,点:向量空间和欧氏空间,向量空间的基、维数和坐标,向量 内积、向量空间的正交基和规范正交基,施密特(Schimidt)方法,正 交矩阵的概念及其性质。 第五章线性方程组 教学重点:线性方程组解的结构和求解的方法。 教学难点:齐次线性方程组、非齐次线性方程组求解的过程。 第六章特征值、特征向量及相似矩阵 教学重点:方阵的特征值、特征向量的概念,特征值、特征向量的性 质,计算特征值和特征向量的方法,相似矩阵的概念、性质。 教学难点:矩阵相似对角化的充分必要条件,矩阵相似对角化的方法, 实对称矩阵的正交相似对角化。 第八章二次型与二次曲面 教学重点:二次型和二次型的矩阵以及二次型的秩,二次型的标准形、 规范形的概念及惯性定理,会用配方法和初等变换法化二次型为标准 形,正定二次型。 教学难点:用正交变换将二次型化为标准形的方法,正定二次型和对 9
9 第四章 n 维向量 教学重点:n 维向量的概念、向量的线性运算、向量的线性组合与线 性表示、向量组的线性相关性的概念;向量组线性相关、线性无关的 有关性质及判别法;向量组极大无关组的概念、求向量组极大无关组 的方法;向量组等价、向量组的秩、矩阵的秩与其行(列)向量组的秩 之间的关系、求向量组秩的方法。 教学难点:向量空间和欧氏空间,向量空间的基、维数和坐标,向量 内积、向量空间的正交基和规范正交基,施密特(Schimidt)方法,正 交矩阵的概念及其性质。 第五章 线性方程组 教学重点:线性方程组解的结构和求解的方法。 教学难点:齐次线性方程组、非齐次线性方程组求解的过程。 第六章 特征值、特征向量及相似矩阵 教学重点:方阵的特征值、特征向量的概念,特征值、特征向量的性 质,计算特征值和特征向量的方法,相似矩阵的概念、性质。 教学难点:矩阵相似对角化的充分必要条件,矩阵相似对角化的方法, 实对称矩阵的正交相似对角化。 第八章 二次型与二次曲面 教学重点:二次型和二次型的矩阵以及二次型的秩,二次型的标准形、 规范形的概念及惯性定理,会用配方法和初等变换法化二次型为标准 形,正定二次型。 教学难点:用正交变换将二次型化为标准形的方法,正定二次型和对

应的正定矩阵的性质以及正定性的判别法。 五、课程教学方法与教学手段 课程教学综合了课堂的讲授、例题和习题、课上和课下的讨论以及课 外资料的查询、分析等方法来传授知识。教学手段主要利用多媒体开 展,以课堂讲授、例题习题练习为主,课外资料查询、分析为辅,可 以利用网络、图书馆进行。 六、 课程教学内容 第一章n阶行列式(8学时) 1.教学内容 (1)n阶行列式的概念: (2)行列式的性质: (3)行列式的展开定理: (4)Cramer法则: 2.重、难点提示 (I)重点:行列式的性质及行列式按行(列)的展开定理、Cramer法则。 (2)难点:行列式的定义,行列式的性质及行列式按行(列)展开定理,一些特殊阶行列 式的计算、Cramer法则的应用。 第二章矩阵(15学时) 1.教学内容 (1)矩阵的概念: (2)矩阵的运算: (3)可逆矩阵: (4)矩阵的初等变换: (5)矩阵的秩: (6)初等矩阵: (T分块矩阵的概念及其运算: (8)分块矩阵的初等变换: 0
10 应的正定矩阵的性质以及正定性的判别法。 五、课程教学方法与教学手段 课程教学综合了课堂的讲授、例题和习题、课上和课下的讨论以及课 外资料的查询、分析等方法来传授知识。教学手段主要利用多媒体开 展,以课堂讲授、例题习题练习为主,课外资料查询、分析为辅,可 以利用网络、图书馆进行。 六、 课程教学内容 第一章 n 阶行列式(8 学时) 1.教学内容 (1)n 阶行列式的概念; (2)行列式的性质; (3)行列式的展开定理; (4)Cramer 法则; 2.重、难点提示 (1)重点:行列式的性质及行列式按行(列)的展开定理、Cramer 法则。 (2)难点:行列式的定义,行列式的性质及行列式按行(列)展开定理,一些特殊 n 阶行列 式的计算、Cramer 法则的应用。 第二章 矩阵(15 学时) 1.教学内容 (1)矩阵的概念; (2)矩阵的运算; (3)可逆矩阵; (4)矩阵的初等变换; (5)矩阵的秩; (6)初等矩阵; (7)分块矩阵的概念及其运算; (8)分块矩阵的初等变换;

2.重、难点提示 (1)重点:矩阵的乘法、矩阵的转置、方阵的行列式及方阵的幂:可逆矩阵、矩阵的初 等变换、矩阵的秩、初等矩阵、矩阵等价的充要条件。 (②)难点:可逆矩阵、矩阵的初等变换、矩阵的秩、初等矩阵、矩阵等价的充要条件及 其应用。 第四章n维向量(10学时) 1.教学内容 (I)n维向量的概念及其线性运算: (2)向量组的线性相关与线性无关: (3)向量组的秩: (4)向量空间: (5)欧氏空间: 2.重、难点提示 (1)重点:向量组的线性相关、线性无关的性质及判别,向量组的极大无关组与秩,向 量空间的基、维数、坐标,坐标变换和基变换,内积、欧氏空间,规范正交基的求法,正交 矩阵。 (2)难点:向量组的线性相关、线性无关的判别,向量组的秩和极大无关组的求法,向 量空间的坐标变换和基变换,规范正交基的求法,正交矩阵。 第五章线性方程组(4学时) 1.教学内容 (1)线性方程组有解的充要条件: (2)线性方程组解的结构: (3)利用矩阵的初等变换解线性方程组: 2.重、难点提示 (1)重点:线性方程组解的结构,齐次线性方程组、非齐次线性方程组的求解。 (2)难点:线性方程组的求解。 第六章特征值、特征向量及相似矩阵(6学时) 1.教学内容 (1)特征值与特征向量: 11
11 2.重、难点提示 (1)重点:矩阵的乘法、矩阵的转置、方阵的行列式及方阵的幂;可逆矩阵、矩阵的初 等变换、矩阵的秩、初等矩阵、矩阵等价的充要条件。 (2)难点:可逆矩阵、矩阵的初等变换、矩阵的秩、初等矩阵、矩阵等价的充要条件及 其应用。 第四章 n 维向量(10 学时) 1.教学内容 (1)n 维向量的概念及其线性运算; (2)向量组的线性相关与线性无关; (3)向量组的秩; (4)向量空间; (5)欧氏空间; 2.重、难点提示 (1)重点:向量组的线性相关、线性无关的性质及判别,向量组的极大无关组与秩,向 量空间的基、维数、坐标,坐标变换和基变换,内积、欧氏空间,规范正交基的求法,正交 矩阵。 (2)难点:向量组的线性相关、线性无关的判别,向量组的秩和极大无关组的求法,向 量空间的坐标变换和基变换,规范正交基的求法,正交矩阵。 第五章 线性方程组(4 学时) 1.教学内容 (1)线性方程组有解的充要条件; (2)线性方程组解的结构; (3)利用矩阵的初等变换解线性方程组; 2.重、难点提示 (1)重点:线性方程组解的结构,齐次线性方程组、非齐次线性方程组的求解。 (2)难点:线性方程组的求解。 第六章 特征值、特征向量及相似矩阵(6 学时) 1.教学内容 (1)特征值与特征向量;
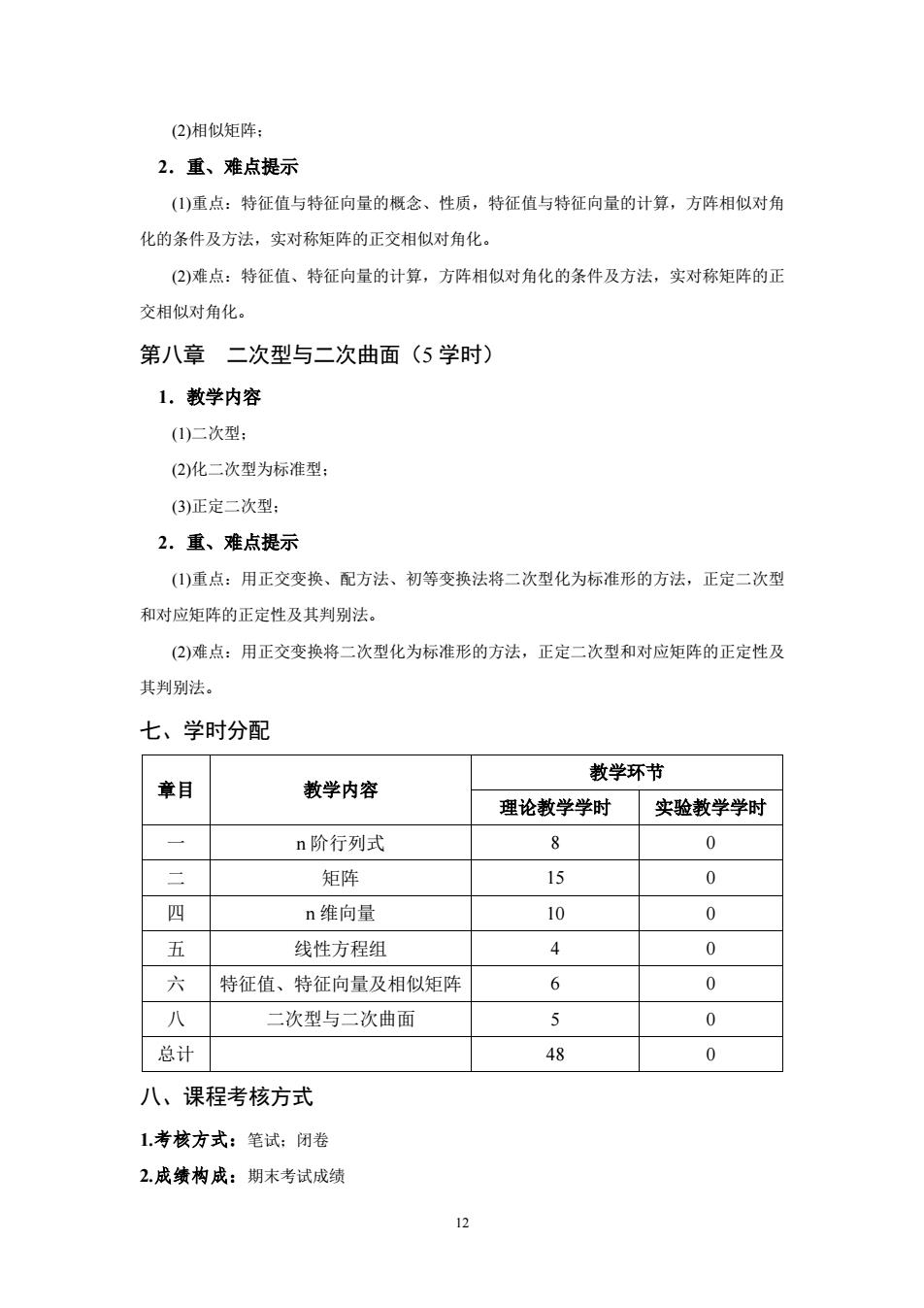
(2)相似矩阵: 2.重、难点提示 (1)重点:特征值与特征向量的概念、性质,特征值与特征向量的计算,方阵相似对角 化的条件及方法,实对称矩阵的正交相似对角化。 (2)难点:特征值、特征向量的计算,方阵相似对角化的条件及方法,实对称矩阵的正 交相似对角化。 第八章二次型与二次曲面(5学时) 1.教学内容 (1)二次型: (2)化二次型为标准型: (3)正定二次型: 2.重、难点提示 (1)重点:用正交变换、配方法、初等变换法将二次型化为标准形的方法,正定二次型 和对应矩阵的正定性及其判别法。 (2)难点:用正交变换将二次型化为标准形的方法,正定二次型和对应矩阵的正定性及 其判别法。 七、学时分配 教学环节 章目 教学内容 理论教学学时 实验教学学时 n阶行列式 8 0 二 矩阵 15 0 四 n维向量 10 0 五 线性方程组 4 0 六 特征值、特征向量及相似矩阵 6 0 八 二次型与二次曲面 5 0 总计 48 0 八、课程考核方式 1考核方式:笔试:闭卷 2.成绩构成:期末考试成绩 12
12 (2)相似矩阵; 2.重、难点提示 (1)重点:特征值与特征向量的概念、性质,特征值与特征向量的计算,方阵相似对角 化的条件及方法,实对称矩阵的正交相似对角化。 (2)难点:特征值、特征向量的计算,方阵相似对角化的条件及方法,实对称矩阵的正 交相似对角化。 第八章 二次型与二次曲面(5 学时) 1.教学内容 (1)二次型; (2)化二次型为标准型; (3)正定二次型; 2.重、难点提示 (1)重点:用正交变换、配方法、初等变换法将二次型化为标准形的方法,正定二次型 和对应矩阵的正定性及其判别法。 (2)难点:用正交变换将二次型化为标准形的方法,正定二次型和对应矩阵的正定性及 其判别法。 七、学时分配 章目 教学内容 教学环节 理论教学学时 实验教学学时 一 n 阶行列式 8 0 二 矩阵 15 0 四 n 维向量 10 0 五 线性方程组 4 0 六 特征值、特征向量及相似矩阵 6 0 八 二次型与二次曲面 5 0 总计 48 0 八、课程考核方式 1.考核方式:笔试;闭卷 2.成绩构成:期末考试成绩