
有限元理论与建模方法 Finite Element Analysis and Modeling 966 无阻尼自由 (K-w2D,=0 特征值问题 振动方程 solve 振动理论 数学 国有频率 2 2. 特征值 Natural frequency 模态频率 01、 …0 共振频率 模态振型 )、{Φ}…{Φn} 特征向量 Modal shape 模态(Mode) 模态参数 动态分析有限元法 2020年9月
有限元理论与建模方法 Finite Element Analysis and Modeling 动态分析有限元法 2020年 9 月 K M 2 0 特征值问题 特征值 特征向量 数学 模态(Mode) solve 1 2 2 2 n 2 、 … 1 2 、 … n 1 、 2 … n 振动理论 模态振型 Modal shape 国有频率 Natural frequency 模态频率 共振频率 模态参数 无阻尼自由 振动方程

有限元理论与建模方法 Finite Element Analysis and Modeling 966 Mode Analysis(模态分析) Analysis of Natural Properties K]-w2M0D,=0 transformation iteration 动态分析有限元法 2020年9月
有限元理论与建模方法 Finite Element Analysis and Modeling 动态分析有限元法 2020年 9 月 Analysis of Natural Properties K M 2 0 ` transformation iteration Mode Analysis(模态分析)

有限元理论与建模方法 Finite Element Analysis and Modeling 966 Modal Analysis(模态分析) 模态频率: 与什么参数有关? 模态振型: 振动形态(形状) [K]-@M=0 动态分析有限元法 2020年9月
有限元理论与建模方法 Finite Element Analysis and Modeling 动态分析有限元法 2020年 9 月 Modal Analysis(模态分析) 模态频率: 模态振型: 与什么参数有关? 振动形态(形状) K M 2 0
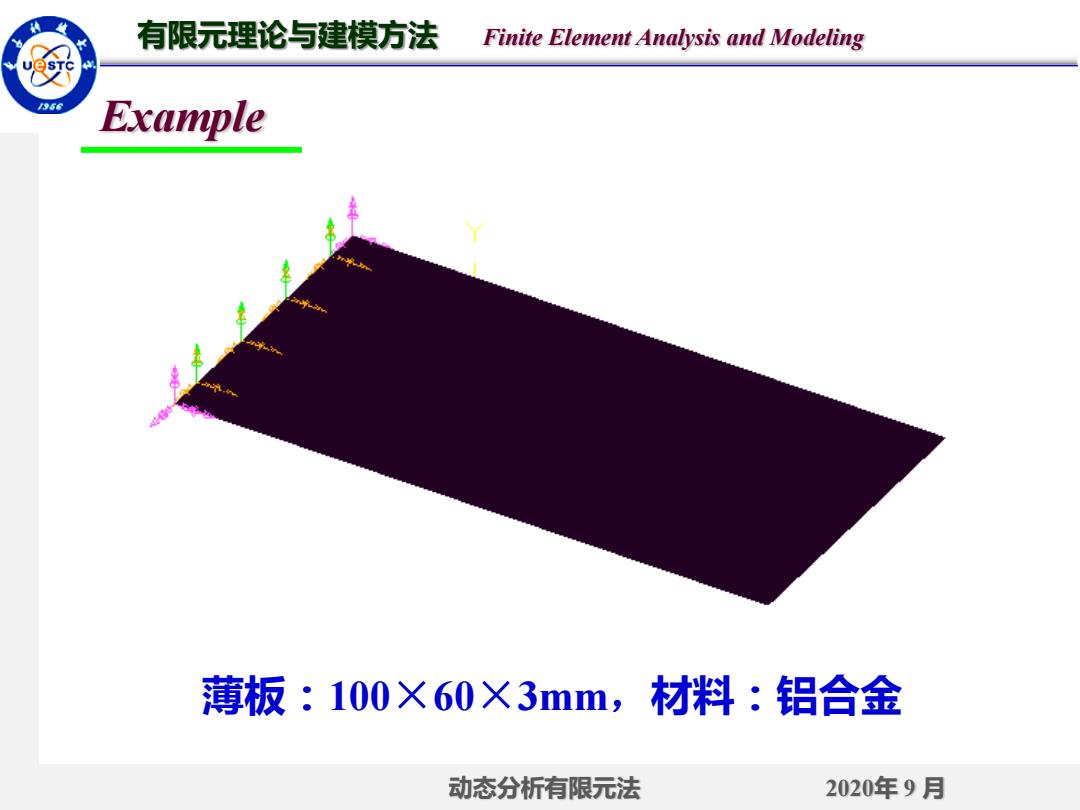
有限元理论与建模方法 Finite Element Analysis and Modeling 9s6 Example 薄板:100×60×3mm,材料:铝合金 动态分析有限元法 2020年9月
有限元理论与建模方法 Finite Element Analysis and Modeling 动态分析有限元法 2020年 9 月 薄板:100×60×3mm,材料:铝合金 Example

有限元理论与建模方法 Finite Element Analysis and Modeling 966 有限元模型 动态分析有限元法 2020年9月
有限元理论与建模方法 Finite Element Analysis and Modeling 动态分析有限元法 2020年 9 月 有限元模型