◆因此,对于中长柱,在设计中应考虑侧向挠度∫对弯矩增大的影响。 (3)长细比10/h>30的长柱 ◆柱的极限荷载发生在荷载增长曲线与截面承载力u-血相关曲线相交之前。 ◆这种破坏为失稳破坏,应进行专门计算。 长柱(失稳破坏) Numei Na M M §6.4偏心受压长柱的二阶弯矩 ◆由干信心历 M=ei(一阶弯矩) ◆由于细长构件产生侧向挠曲 M-Nei+Ny=N(ei+y) Mmax-Nei +Nf-N (ei +f) M'=Ny- 二阶弯矩(二阶效应) ◆在截面和初始偏心距相同的情况下,柱的长细比0h不同,侧向挠度∫的大小 不同,影响程度会有很大差别,将产生不同的破坏类型
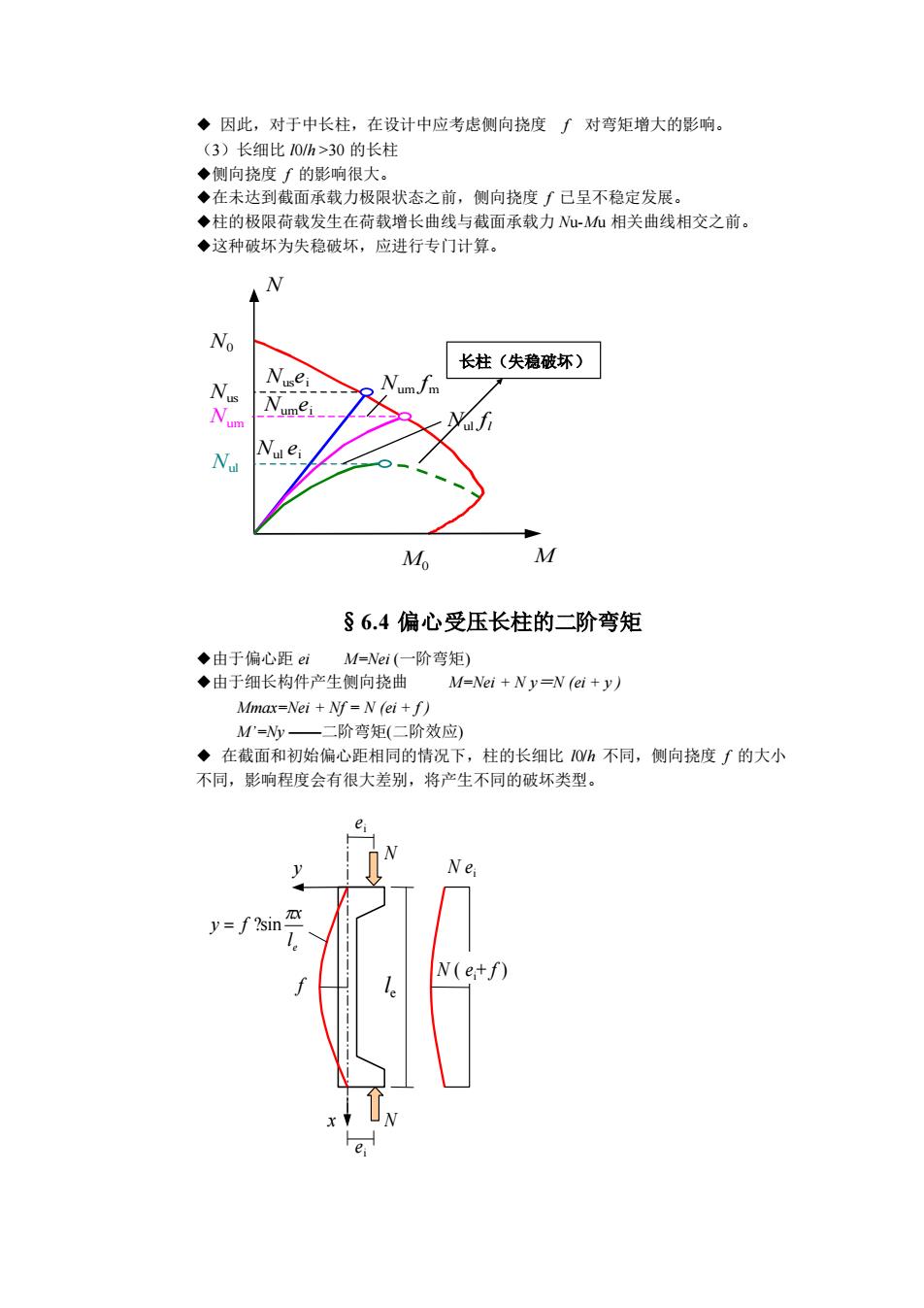
◆ 因此,对于中长柱,在设计中应考虑侧向挠度 f 对弯矩增大的影响。 (3)长细比 l0/h >30 的长柱 ◆侧向挠度 f 的影响很大。 ◆在未达到截面承载力极限状态之前,侧向挠度 f 已呈不稳定发展。 ◆柱的极限荷载发生在荷载增长曲线与截面承载力 Nu-Mu 相关曲线相交之前。 ◆这种破坏为失稳破坏,应进行专门计算。 §6.4 偏心受压长柱的二阶弯矩 ◆由于偏心距 ei M=Nei (一阶弯矩) ◆由于细长构件产生侧向挠曲 M=Nei + N y=N (ei + y ) Mmax=Nei + Nf = N (ei + f ) M’=Ny ——二阶弯矩(二阶效应) ◆ 在截面和初始偏心距相同的情况下,柱的长细比 l0/h 不同,侧向挠度 f 的大小 不同,影响程度会有很大差别,将产生不同的破坏类型。 e l x y f = ?sin f y x ei ei N N N ei N ( ei+ f ) l e M N N0 M0 Nus Nus ei Num Numei Num fm Nul Nul ei Nul fl 长柱(失稳破坏)
◆对于长细比较大的构件,二阶效应引起的弯矩不能忽略。 e y=f?sin e 刀=9H=141 e e, 了号成5 k=0033×125+0017.11 h 171.7h =564.61-54,5=15-00哈 N ho
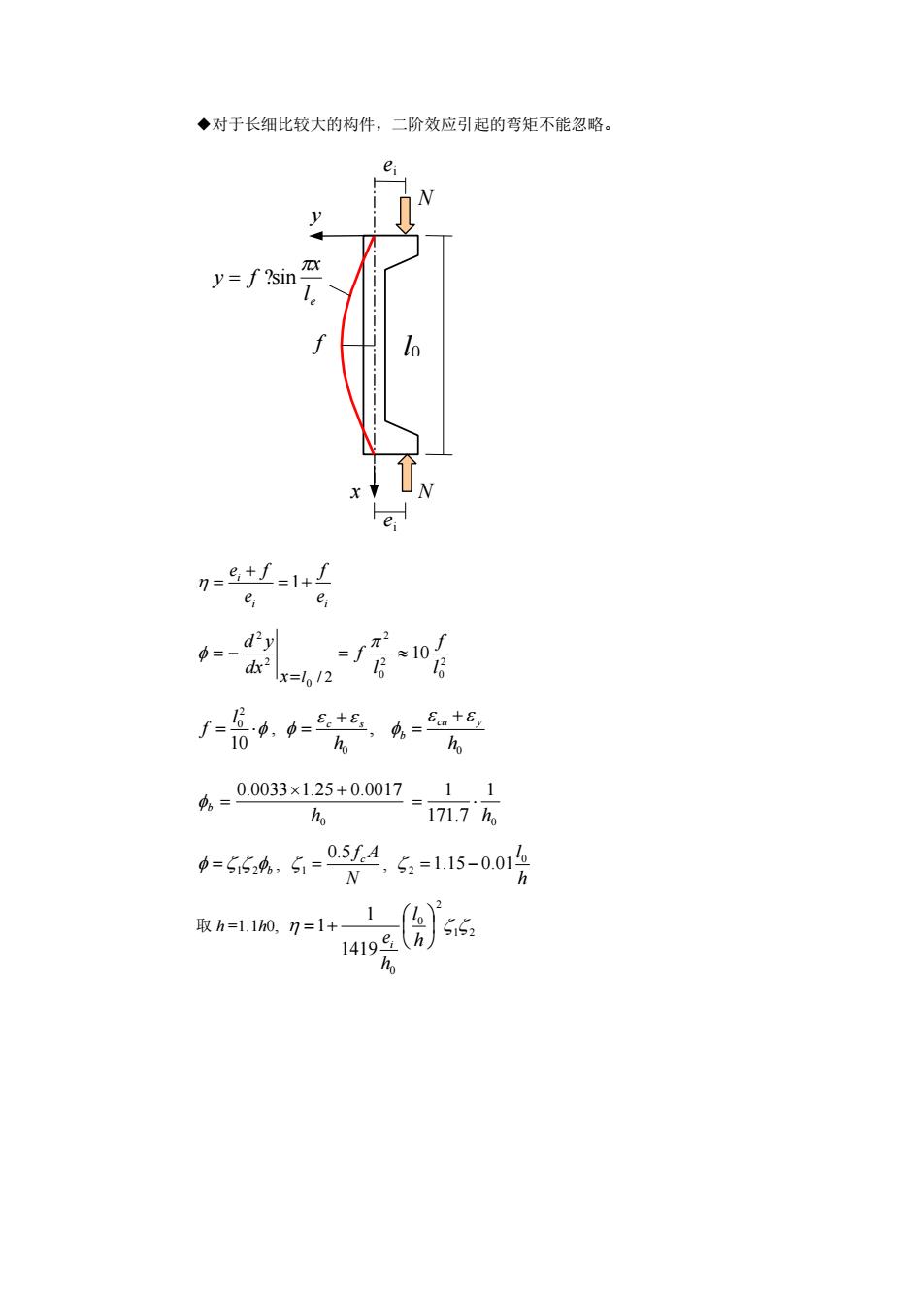
◆对于长细比较大的构件,二阶效应引起的弯矩不能忽略。 i i i e f e e f = + + = 1 10 2 0 2 0 2 0 2 2 / 2 l f l f x dx d y l = = = − = 10 2 0 l f , 0 0 , h h cu y b c s + = + = 1 171.7 1 0.0033 1.25 0.0017 h0 h0 b = + = = 1 2b , N 0.5 f cA 1 = , h l 0 2 =1.15 − 0.01 取 h =1.1h0, 1 2 2 0 0 1419 1 1 = + h l h ei e l x y f = ?sin f y x ei ei N N l l0 e
y=f?sin .UN 偏心距增大系数)=S+L。1 e, e 4 h 4=003×125+0017.1.1 171.7h 0=56.6-0545=115-01哈 §6.5矩形截面偏心受压构件正截面承载力计算公式 偏心受压正截面受力分析方法与受弯情况是相同。 ◆采用以平截面假定为基础的计算理论。 ◆采用混凝士和钢筋的应力-应变关系模型, ·对受压区混凝土采用等效矩形应力图。 ◆等效矩形应力图的强度为a1心,等效矩形应力图的高 度x与中和轴高度xn的比值为b1
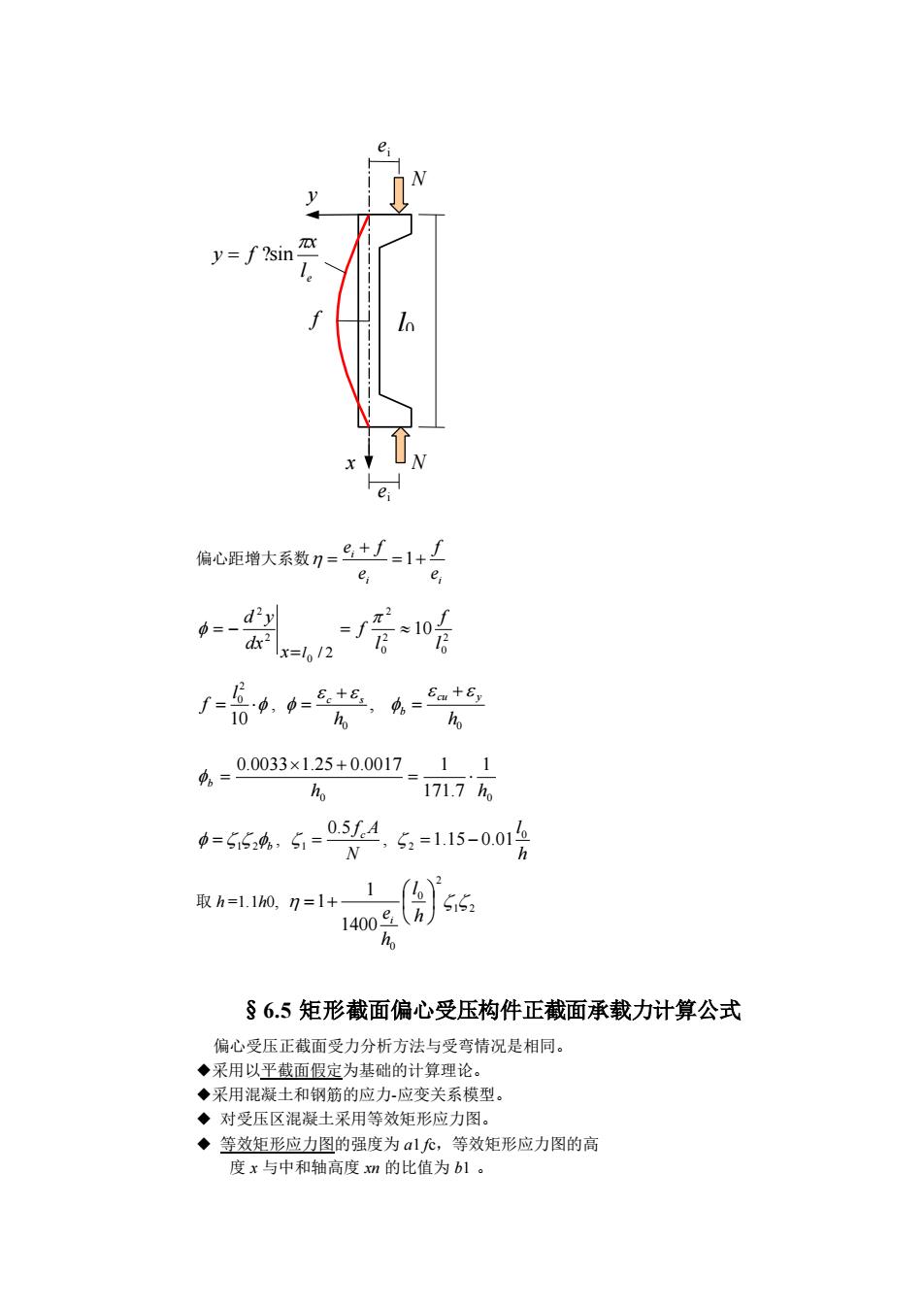
偏心距增大系数 i i i e f e e f = + + = 1 10 2 0 2 0 2 0 2 2 / 2 l f l f x dx d y l = = = − = 10 2 0 l f , 0 0 , h h cu y b c s + = + = 1 171.7 0.0033 1.25 0.0017 1 h0 h0 b = + = = 1 2b , N 0.5 f cA 1 = , h l 0 2 =1.15 − 0.01 取 h =1.1h0, 1 2 2 0 0 1400 1 1 = + h l h ei §6.5 矩形截面偏心受压构件正截面承载力计算公式 偏心受压正截面受力分析方法与受弯情况是相同。 ◆采用以平截面假定为基础的计算理论。 ◆采用混凝土和钢筋的应力-应变关系模型。 ◆ 对受压区混凝土采用等效矩形应力图。 ◆ 等效矩形应力图的强度为 a1 fc,等效矩形应力图的高 度 x 与中和轴高度 xn 的比值为 b1 。 e l x y f = ?sin f y x ei ei N N l l0 e
M M GA. A A A 当x≤b时一受拉破坏(大偏心受压) N。=afbx+fA-f,4 M.=ah9-+49-a,)+9-a) 当x>地时一受压破坏(小偏心受压) N。=afbr+fA-o,A M.=af克+a49-a)+9-) CL ho ‘远纵向力一侧钢筋应力s 由平截面假定可得 6于 盟0,=5A-=- ho-xn xn x/h N.=af bx+fA-G,A, M.=abx传-勇+o,4传-a)+5-a 采用上式基本公式会出现x的三次方程
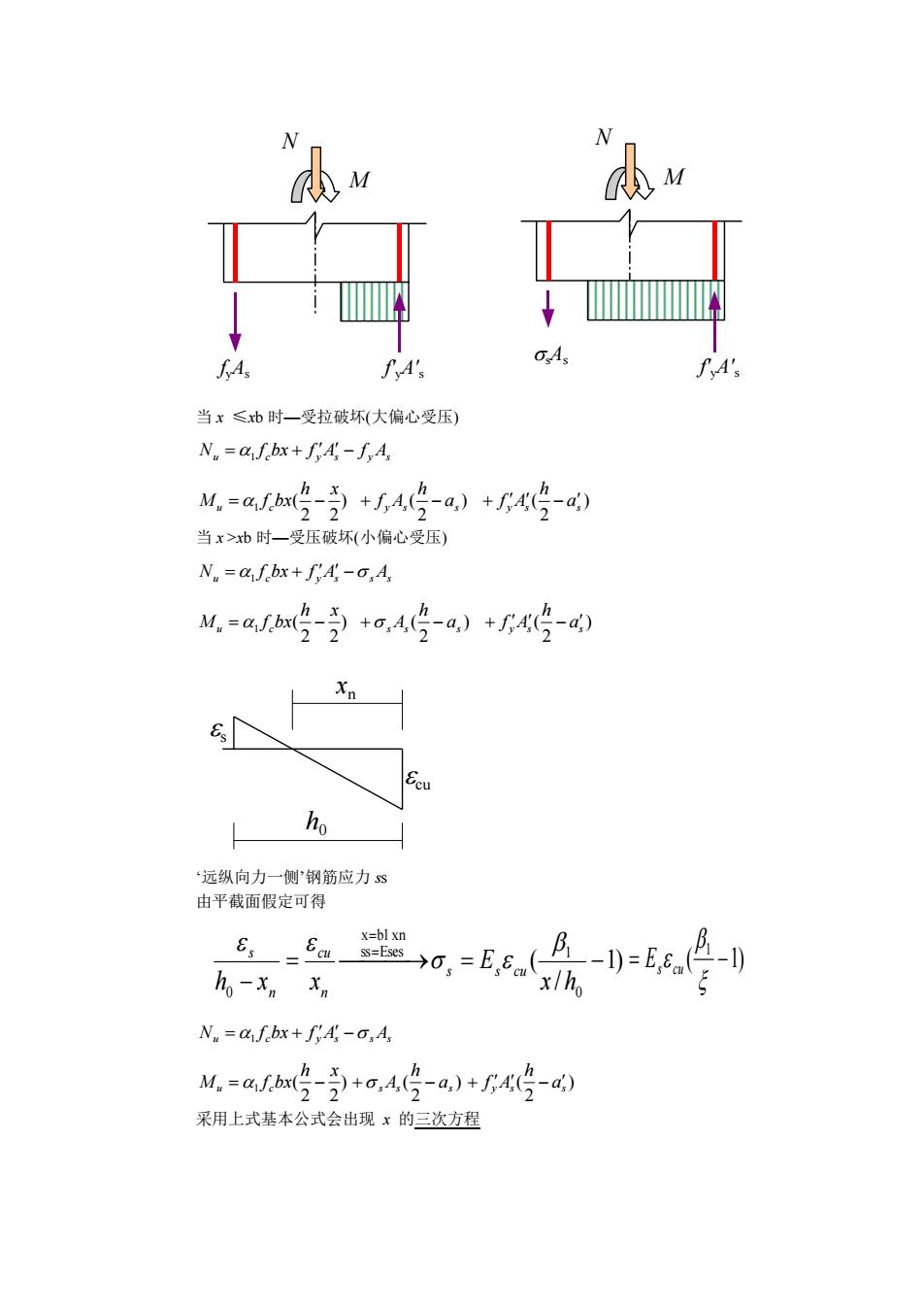
当 x ≤xb 时—受拉破坏(大偏心受压) u 1 c y s yAs N = f bx + f A − f ) 2 2 ( 1 h x M f bx u = c − ) 2 ( y s as h + f A − ) 2 ( y s as h + f A − 当 x >xb 时—受压破坏(小偏心受压) u 1 c yAs sAs N = f bx + f − ) 2 2 ( 1 h x M f bx u = c − ) 2 ( s s as h + A − ) 2 ( y s as h + f A − ‘远纵向力一侧’钢筋应力 ss 由平截面假定可得 1) / ( 0 ss Eses 1 x b1 xn 0 = ⎯⎯⎯→ = − − = = x h E h x x s s cu n cu n s ( 1) 1 = − Es cu u 1 c yAs sAs N = f bx + f − ) 2 2 ( 1 h x M f bx u = c − ) 2 ( s s as h + A − ) 2 ( y s as h + f A − 采用上式基本公式会出现 x 的三次方程 cu s xn h0 sAs f'yA' s N M fyAs f'yA' s N M
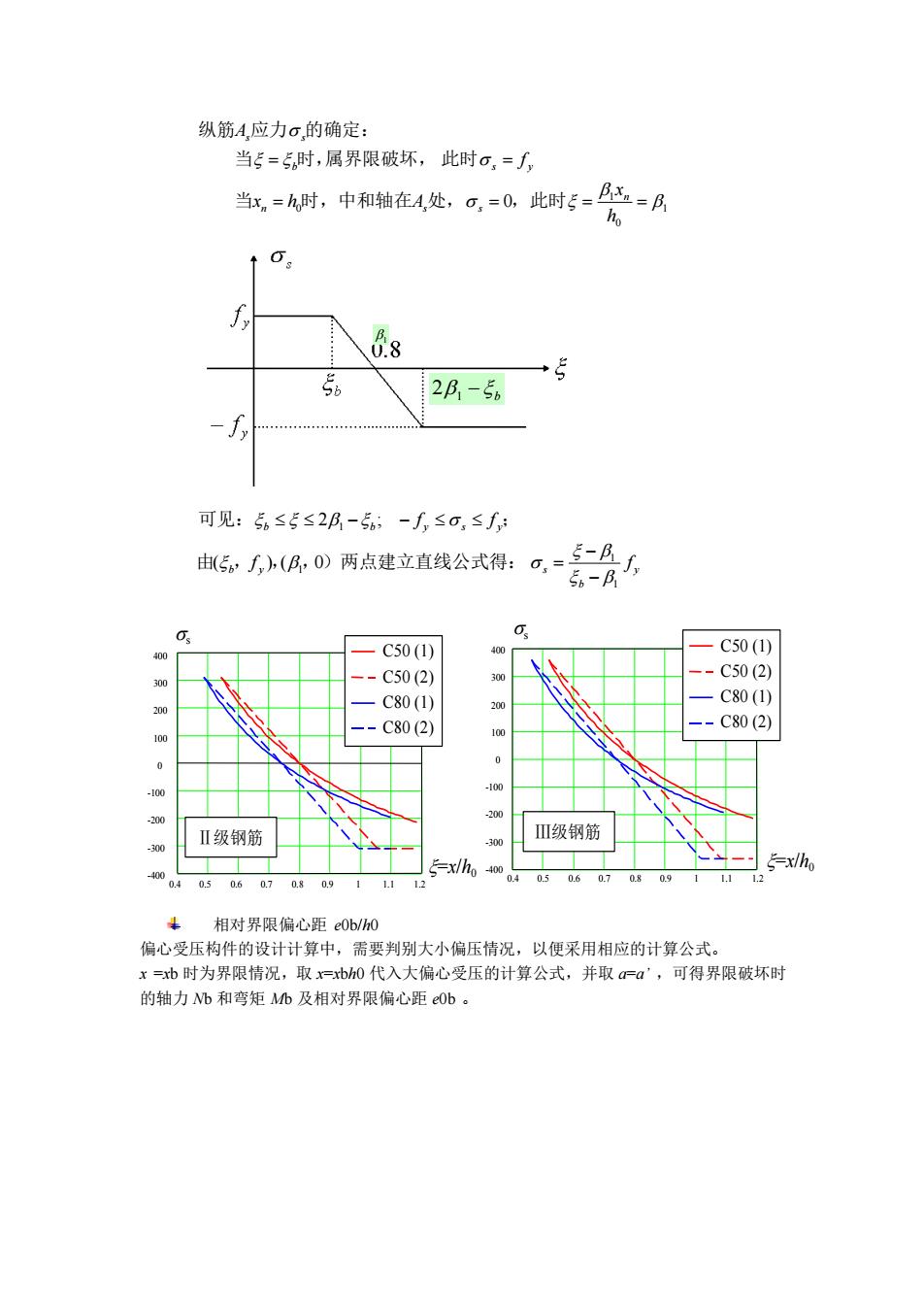
纵筋4,应力σ的确定: 当5=5时,属界限破坏,此时。,=了, 当多=A时,中和轴在处,g=0此时5=货=A f +5 2B-56 Jy 可见:5≤5≤2月-5;-f,≤o,≤f 6月以0两点建立直线公式得:a一系二层 C50(1) 一C50(1) .C502) -C50(2 -C801) 20 C80(1) -C80(2) -C802) 100 Ⅱ级钢筋 Ⅲ级钢筋 E-x/ho 0506070809 相对界限偏心距eOh0 偏心受压构件的设计计算中,需要判别大小偏压情况,以便采用相应的计算公式 x=b时为界限情况,取=bh0代入大偏心受压的计算公式,并取Fa',可得界限破坏时 的轴力b和弯矩Mb及相对界限偏心距Ob
1 0 1 0 0 = = = = = = h x x h A f A n n s s b s y s s 当 时,中和轴在 处, ,此时 当 时,属界限破坏, 此时 纵筋 应力 的确定: y b b y s b b y s y f f f f 1 1 1 1 ( ) ( 0 2 ; − − = − − 由 , , ,)两点建立直线公式得: 可见: ; 相对界限偏心距 e0b/h0 偏心受压构件的设计计算中,需要判别大小偏压情况,以便采用相应的计算公式。 x =xb 时为界限情况,取 x=xbh0 代入大偏心受压的计算公式,并取 a=a’ ,可得界限破坏时 的轴力 Nb 和弯矩 Mb 及相对界限偏心距 e0b 。 0.4 0.5 0.6 0.7 0.8 0.9 1 1.1 1.2 -400 -300 -200 -100 0 100 200 300 400 C50 (1) C50 (2) C80 (1) C80 (2) =x/h0 s Ⅱ级钢筋 0.4 0.5 0.6 0.7 0.8 0.9 1 1.1 1.2 -400 -300 -200 -100 0 100 200 300 400 =x/h0 s C50 (1) C50 (2) C80 (1) C80 (2) Ⅲ级钢筋 1 21 − b