便施工。 作业:6-1(0=H, N=1450kN) 6-2(D=350mm,N-2500kN,Cmin=30mm) §6.3偏心受压构件正截面受压破坏形态 N eo M-N eo 压弯构件 偏心受压构件 A? -ho- 偏心距0=0时,即M0一一轴压构件 当e0一0时,即0一一受弯构件 偏心受压构件的受力性能和破坏形态界于轴压构件和受弯构件之间。 一、偏心受压短柱的破坏形态 偏压构件破坏形态与偏心距0和纵向钢筋配筋率有关。 I、受拉破坏tensile failure 产生受拉破坏的条件:偏心距0较大,且受拉侧纵向钢筋配筋合适
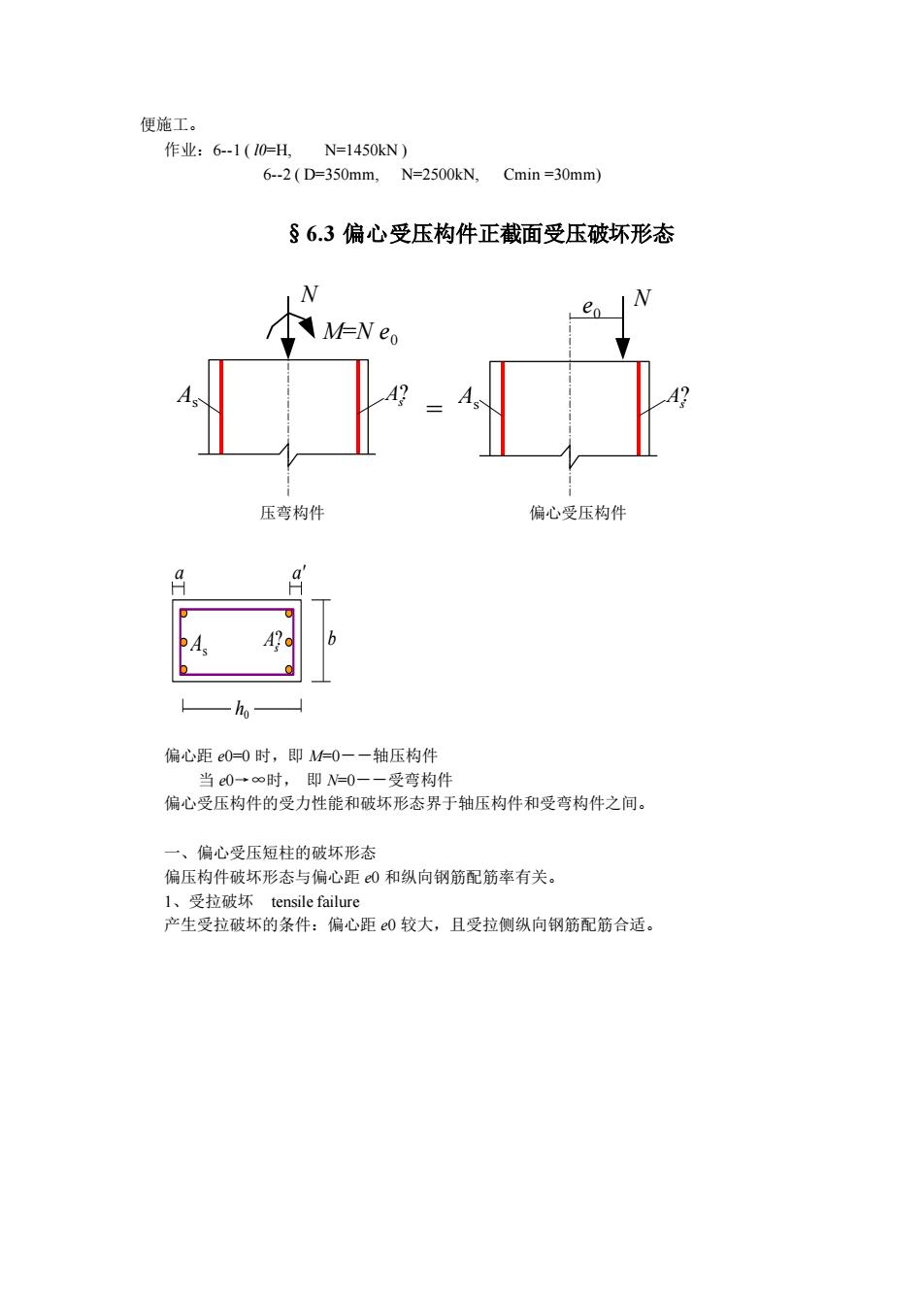
便施工。 作业:6-1 ( l0=H, N=1450kN ) 6-2 ( D=350mm, N=2500kN, Cmin =30mm) §6.3 偏心受压构件正截面受压破坏形态 压弯构件 偏心受压构件 偏心距 e0=0 时,即 M=0--轴压构件 当 e0→∞时, 即 N=0--受弯构件 偏心受压构件的受力性能和破坏形态界于轴压构件和受弯构件之间。 一、偏心受压短柱的破坏形态 偏压构件破坏形态与偏心距 e0 和纵向钢筋配筋率有关。 1、受拉破坏 tensile failure 产生受拉破坏的条件:偏心距 e0 较大,且受拉侧纵向钢筋配筋合适。 As As ? h0 a a' b = M=N e0 N As As ? e N 0 As As ?
M A A fA's M较大,N较小 偏心距0较大 ◆截面远纵向力一侧混凝土较早出现裂缝,5的应力随荷载增加发展较快,首先达到 屈服。 ◆此后,裂缝迅速开展,受压区高度减小。 ◆最后近纵向力一侧钢筋A5受压屈服,压区混凝土压碎而达到破坏。 ◆这种破坏具有明显预兆,变形能力较大,承载力主要取决于受拉侧钢筋 ◆受压破坏 般为偏心距0较大,且受拉侧纵向钢筋配筋适当, 通常称为大偏心受压。 与双筋矩形截面梁相似? 4破坏特征:受拉钢筋先屈服,然后受压区混凝土被压碎, 此时,受压钢筋也达到屈服。(塑性破坏性质) 2、受压破坏compressive failure 产生受压破坏的条件: (I)相对偏心距O/0较小。 (2)相对偏心距0/0较大,但远纵向力一侧纵筋As配置较多
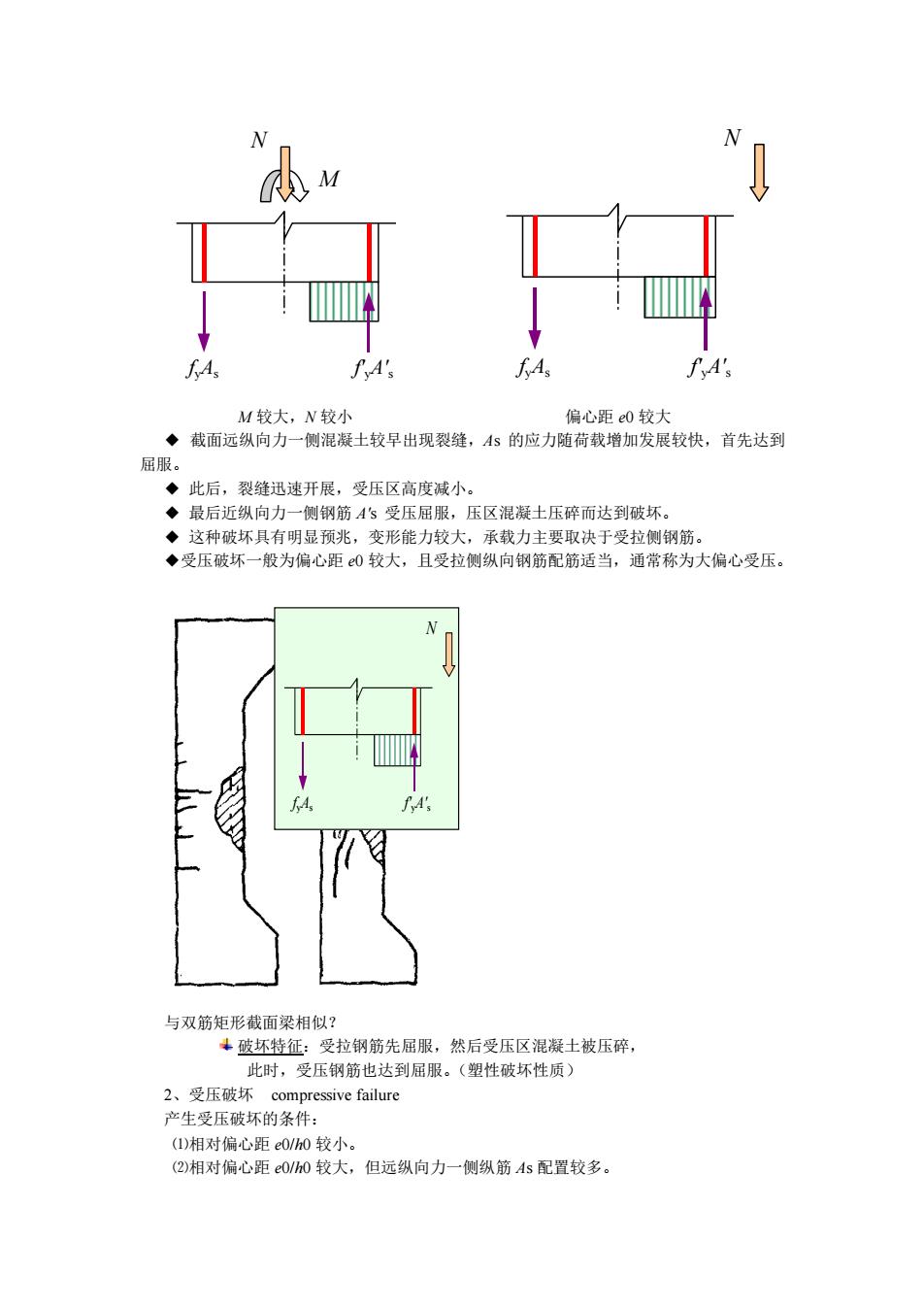
M 较大,N 较小 偏心距 e0 较大 ◆ 截面远纵向力一侧混凝土较早出现裂缝,As 的应力随荷载增加发展较快,首先达到 屈服。 ◆ 此后,裂缝迅速开展,受压区高度减小。 ◆ 最后近纵向力一侧钢筋 A's 受压屈服,压区混凝土压碎而达到破坏。 ◆ 这种破坏具有明显预兆,变形能力较大,承载力主要取决于受拉侧钢筋。 ◆受压破坏一般为偏心距 e0 较大,且受拉侧纵向钢筋配筋适当,通常称为大偏心受压。 与双筋矩形截面梁相似? 破坏特征:受拉钢筋先屈服,然后受压区混凝土被压碎, 此时,受压钢筋也达到屈服。(塑性破坏性质) 2、受压破坏 compressive failure 产生受压破坏的条件: ⑴相对偏心距 e0/h0 较小。 ⑵相对偏心距 e0/h0 较大,但远纵向力一侧纵筋 As 配置较多。 f yAs f'yA' s N f yAs f'yA' s N M fyAs f'yA's N
◆截面近纵向力一侧混凝土和钢筋的受力较大。远纵向力一侧钢筋应力较小。 ◆当相对偏心距eO0很小时,远纵向力一侧还可能出现受压情况。 ◆截面最后是由于受压区混凝土首先压碎而达到破坏,远纵向力一侧钢筋未达到屈服, 破坏且右脆性性历 ◆承载力主要取决于压区混凝土和近纵向力一侧钢筋 ◆A5太多的情况在设计应予避免,因此受压破坏一般为偏心距较小的情况,故常称为 小偏心受压。 +破坏特征:受压区混凝土先被压碎,近纵向力一侧钢筋达到屈服,而远纵向力 一侧钢筋,不论受拉还是受压,均达不到屈服。(脆性破坏性质)
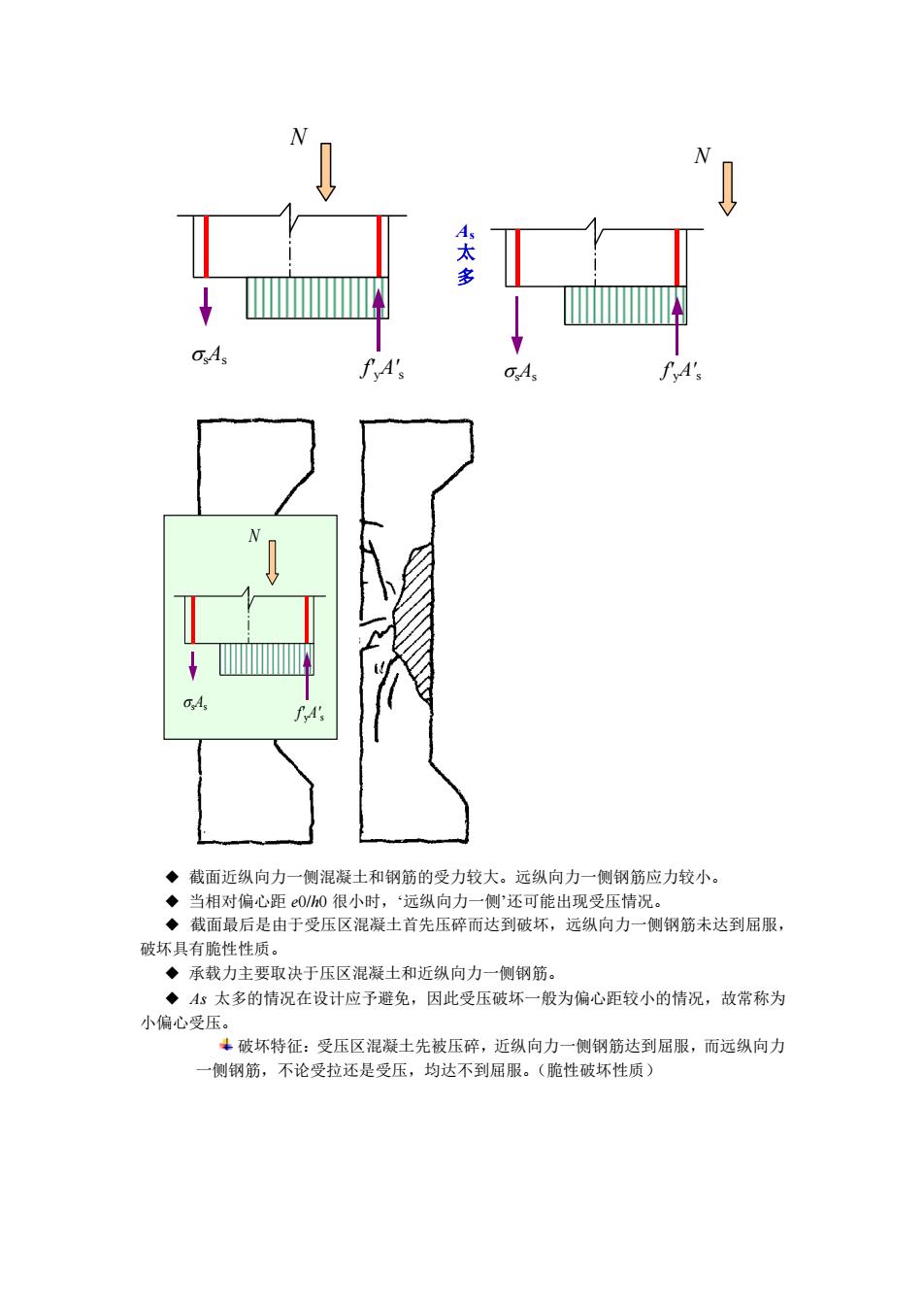
◆ 截面近纵向力一侧混凝土和钢筋的受力较大。远纵向力一侧钢筋应力较小。 ◆ 当相对偏心距 e0/h0 很小时,‘远纵向力一侧’还可能出现受压情况。 ◆ 截面最后是由于受压区混凝土首先压碎而达到破坏,远纵向力一侧钢筋未达到屈服, 破坏具有脆性性质。 ◆ 承载力主要取决于压区混凝土和近纵向力一侧钢筋。 ◆ As 太多的情况在设计应予避免,因此受压破坏一般为偏心距较小的情况,故常称为 小偏心受压。 破坏特征:受压区混凝土先被压碎,近纵向力一侧钢筋达到屈服,而远纵向力 一侧钢筋,不论受拉还是受压,均达不到屈服。(脆性破坏性质) sAs f'yA' s N sAs f'yA' s N As 太 多 sAs f'yA' s N
受拉破坏 受压破坏 3、受拉破坏和受压破坏的界限 ◆受拉钢筋屈服的同时受压区混凝土边缘达到极限压应变℃u ◆与话筋梁和超筋梁的界限情况类似,相对界限受压区高度: 5≤。—→受拉破坏(大偏压破坏) >。—→受压破坏(小偏压破坏 (仁人、偏心受压长柱的破坏形态 L.附加偏心距a 为考虑施工误差、计算偏差及材料的不均匀等因素的不利影响,引入附加偏心距 之和东药有柔力汁草中,用心E爽计算心能小与心流 e,=eo+es ea=20mm与h/30两者中的较大值 h指偏心方向的截面尺寸 2长柱的受力线性 (1)长细比10M≤5的短柱 (0≤17.5) ◆柱侧向挠度∫与初始偏心距:相比很小。 ◆柱跨中弯矩Mer+)随轴力N的增加基本呈线性增长。 ◆直至达到截面承载力极限状态产生破坏。 短柱可忽略侧向挠度∫的影响
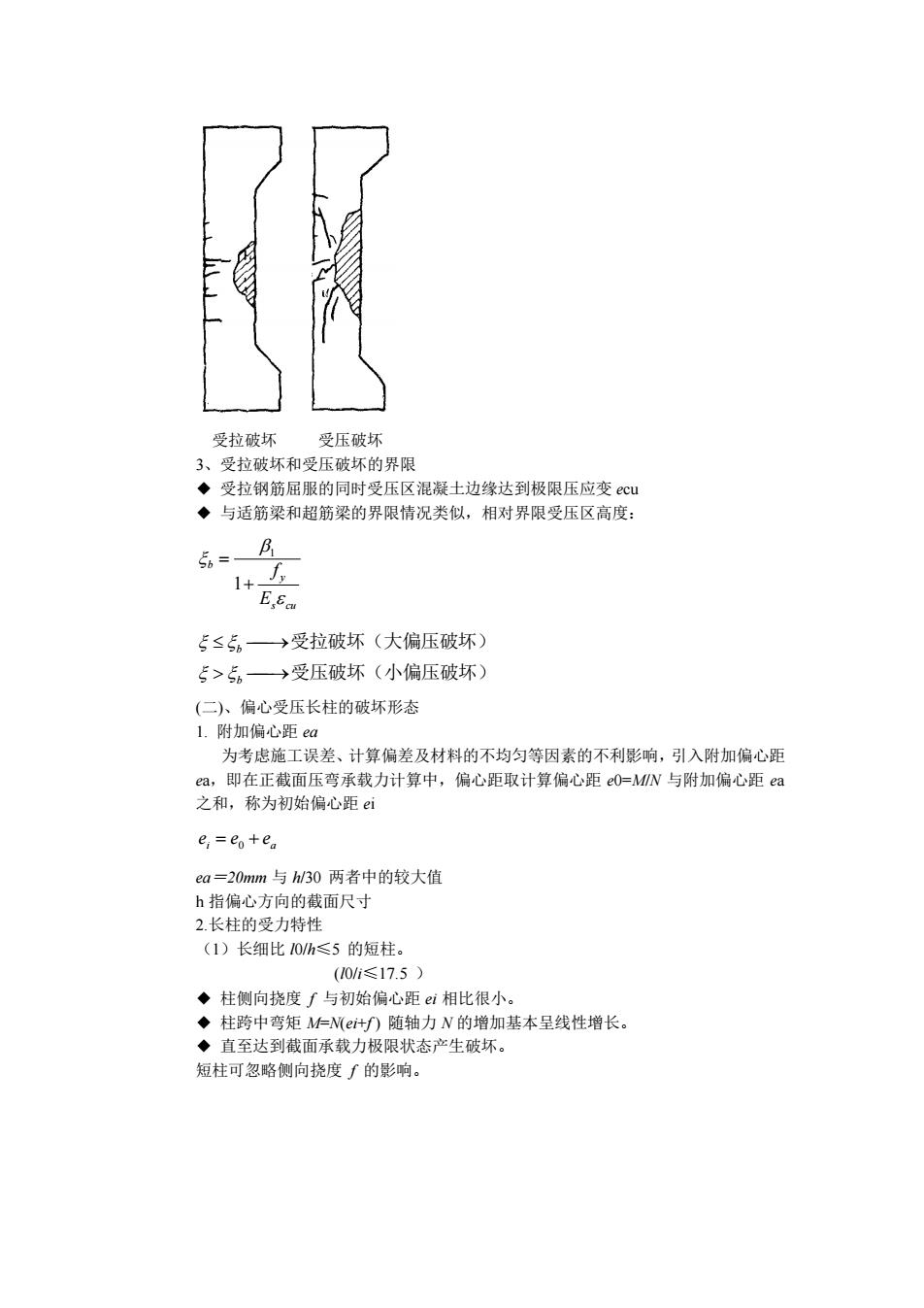
受拉破坏 受压破坏 3、受拉破坏和受压破坏的界限 ◆ 受拉钢筋屈服的同时受压区混凝土边缘达到极限压应变 ecu ◆ 与适筋梁和超筋梁的界限情况类似,相对界限受压区高度: s cu y b E f + = 1 1 受压破坏(小偏压破坏) 受拉破坏(大偏压破坏) ⎯→ ⎯→ b b (二)、偏心受压长柱的破坏形态 1. 附加偏心距 ea 为考虑施工误差、计算偏差及材料的不均匀等因素的不利影响,引入附加偏心距 ea,即在正截面压弯承载力计算中,偏心距取计算偏心距 e0=M/N 与附加偏心距 ea 之和,称为初始偏心距 ei i a e = e + e 0 ea=20mm 与 h/30 两者中的较大值 h 指偏心方向的截面尺寸 2.长柱的受力特性 (1)长细比 l0/h≤5 的短柱。 (l0/i≤17.5 ) ◆ 柱侧向挠度 f 与初始偏心距 ei 相比很小。 ◆ 柱跨中弯矩 M=N(ei+f ) 随轴力 N 的增加基本呈线性增长。 ◆ 直至达到截面承载力极限状态产生破坏。 短柱可忽略侧向挠度 f 的影响

短柱(材料破环) N M M (2)长细比10/h=5-30的中长柱】 ◆侧向挠度∫与et相比不能忽略 ◆∫随轴力增大而增大,柱跨中弯矩M=N(i+)的增长速度大于轴力N的增长 速度。 ◆即M随N的增加呈明显的非线性增长。 No 中长柱(材料破坏) N Nu./m Nw ul e, M M ◆虽然最终柱在M和N的共同作用下达到截面承载力极限状态,但承载力明显低 于同样截面和初始偏心距的短柱
(2)长细比 l0/h =5~30 的中长柱。 ◆侧向挠度 f 与 ei 相比不能忽略 ◆ f 随轴力增大而增大,柱跨中弯矩 M = N ( ei + f ) 的增长速度大于轴力 N 的增长 速度。 ◆ 即 M 随 N 的增加呈明显的非线性增长。 ◆ 虽然最终柱在 M 和 N 的共同作用下达到截面承载力极限状态,但承载力明显低 于同样截面和初始偏心距的短柱。 M N N0 M0 Nus Nus ei Num Numei Num fm Nul Nul ei Nul fl M N N0 M0 Nus Nus ei Num Numei Num fm Nul Nul ei Nul fl 短柱(材料破坏) 中长柱(材料破坏)