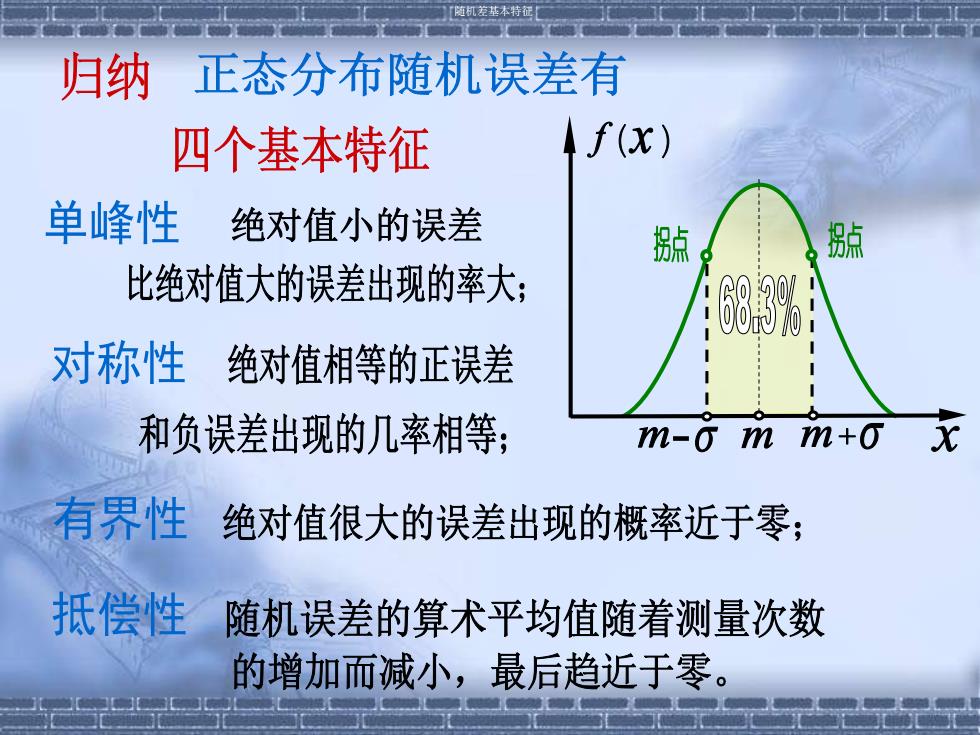
「随机差基本特征 归纳 正态分布随机误差有 四个基本特征 4f(x) 单峰性 绝对值小的误差 號 號 比绝对值大的误差出现的率大; 对称性 绝对值相等的正误差 和负误差出现的几率相等; m-o m m+o x 有界性 绝对值很大的误差出现的概率近于零 抵偿性 随机误差的算术平均值随着测量次数 的增加而减小,最后趋近于零
随机差基本特征

实验值及平均值的标准偏差概念 实际上测量次数总是有限的,在大学物理实验中, 通常取5≤n≤10,一般采用下述定义式进行评估 测量值的算数平均值 x- 六含x 单次实验值的标准偏差 Sx= (x-元)2 =1 n-1 (表征随机误差引起测得值,的分散性) 平均值的实验标准偏差Sx= (X-元)2 n(n-1) (表征同一被测量的各个测量列平均值的分散性)
标准偏差

二、测量不确定度的基本概念
二、不确定度概念

误差 一理论上是对真值而言 真值 一般不可能准确知道 因此,误差无法按其定义式精确求出, 不应将任何一个确定的已知值称作误差。 现实可行的办法就只能根据测量数据和 测量条件进行推算(包括统计推算和其它推算), 去求得误差的估计值。 误差的估计值或数值指标应采用另一个专门名称, 这个名称就是不确定度
必要性

不确定度通常用U表示。 用来表征被测量的真值所处的量值散布范围内的评定。 即表示由于测量误差的存在而对被测量值不能确定的程度。 不确定度所反映的是可能存在的误差分布范围, 即随机误差分量和未定系差分量的联合分布范围。 某个被测量X的直接测量结果表达式: X=x±U 表示真值在区间(元-U,x+U)内的概率约等于或大于0.95
定义