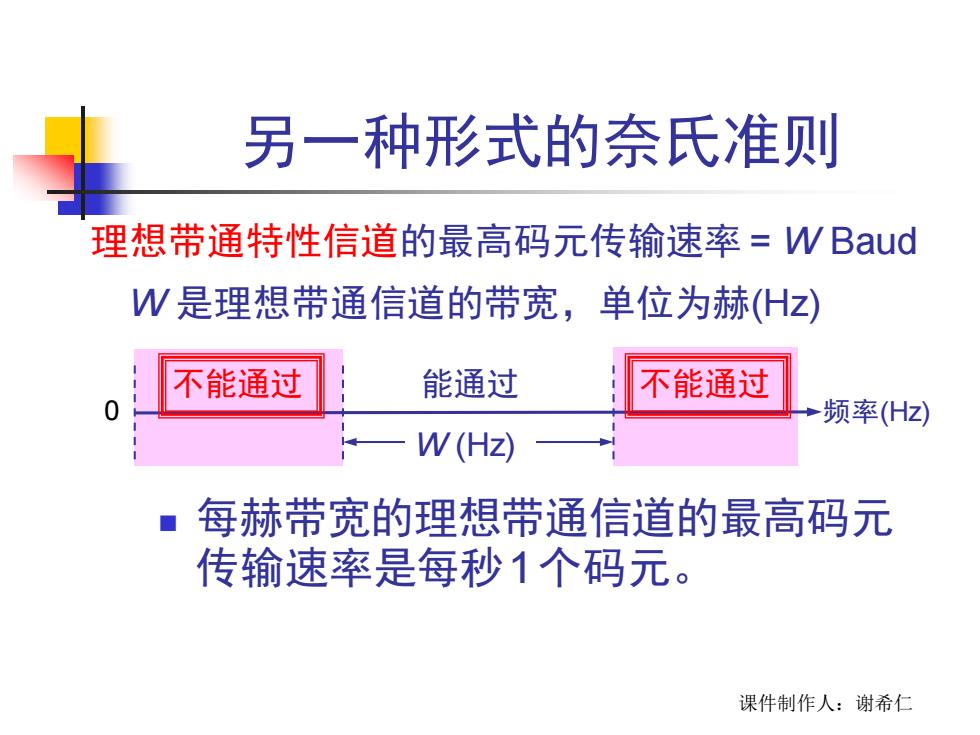
另一种形式的奈氏准则 理想带通特性信道的最高码元传输速率=V Baud W是理想带通信道的带宽,单位为赫(Hz) 不能通过 能通过 不能通过 频率(Hz) W(Hz) 每赫带宽的理想带通信道的最高码元 传输速率是每秒1个码元。 课件制作人:谢希仁
课件制作人:谢希仁 另一种形式的奈氏准则 ◼ 每赫带宽的理想带通信道的最高码元 传输速率是每秒1个码元。 理想带通特性信道的最高码元传输速率 = W Baud W 是理想带通信道的带宽,单位为赫(Hz) 能通过 不能通过 0 频率(Hz) W (Hz) 不能通过

在任何信道中,码元传输的速率是有上 限的,否测就会出现码间串扰的问题, 使接收端对码元的判决(即识别)成为 不可能。 如果信道的频带越宽,也就是能够通过 的信号高频分量越多,那么就可以用更 高的速率传送码元而不出现码间串扰。 课件制作人:谢希仁
课件制作人:谢希仁 ◼ 在任何信道中,码元传输的速率是有上 限的,否则就会出现码间串扰的问题, 使接收端对码元的判决(即识别)成为 不可能。 ◼ 如果信道的频带越宽,也就是能够通过 的信号高频分量越多,那么就可以用更 高的速率传送码元而不出现码间串扰

(2)信噪比 香农(Shannon)用信息论的理论推导出了 带宽受限且有高斯白噪声干扰的信道的 极限、无差错的信息传输速率。 ■信道的极限信息传输速率C可表达为 C=Wlog2(1+S/N)b/s ■W为信道的带宽(以Hz为单位); ·S为信道内所传信号的平均功率; ·N为信道内部的高斯噪声功率。 课件制作人:谢希仁
课件制作人:谢希仁 (2) 信噪比 ◼ 香农(Shannon)用信息论的理论推导出了 带宽受限且有高斯白噪声干扰的信道的 极限、无差错的信息传输速率。 ◼ 信道的极限信息传输速率 C 可表达为 ◼ C = W log2 (1+S/N) b/s ◼ W 为信道的带宽(以 Hz 为单位); ◼ S 为信道内所传信号的平均功率; ◼ N 为信道内部的高斯噪声功率

香农公式表明 信道的带宽或信道中的信噪比越大,则信息的 极限传输速率就越高。 ■ 只要信息传输速率低于信道的极限信息传输速 率,就一定可以找到某种办法来实现无差错的 传输。 ■若信道带宽W或信噪比SW没有上限(当然实 际信道不可能是这样的),则信道的极限信息 传输速率C也就没有上限。 ■实际信道上能够达到的信息传输速率要比香农 的极限传输速率低不少。 课件制作人:谢希仁
课件制作人:谢希仁 香农公式表明 ◼ 信道的带宽或信道中的信噪比越大,则信息的 极限传输速率就越高。 ◼ 只要信息传输速率低于信道的极限信息传输速 率,就一定可以找到某种办法来实现无差错的 传输。 ◼ 若信道带宽W或信噪比S/N 没有上限(当然实 际信道不可能是这样的),则信道的极限信息 传输速率C 也就没有上限。 ◼ 实际信道上能够达到的信息传输速率要比香农 的极限传输速率低不少

请注意 对于频带宽度已确定的信道,如果信噪 比不能再提高了,并且码元传输速率也 达到了上限值,那么还有办法提高信息 的传输速率。这就是用编码的方法让每 一个码元携带更多比特的信息量。 课件制作人:谢希仁
课件制作人:谢希仁 请注意 ◼ 对于频带宽度已确定的信道,如果信噪 比不能再提高了,并且码元传输速率也 达到了上限值,那么还有办法提高信息 的传输速率。这就是用编码的方法让每 一个码元携带更多比特的信息量