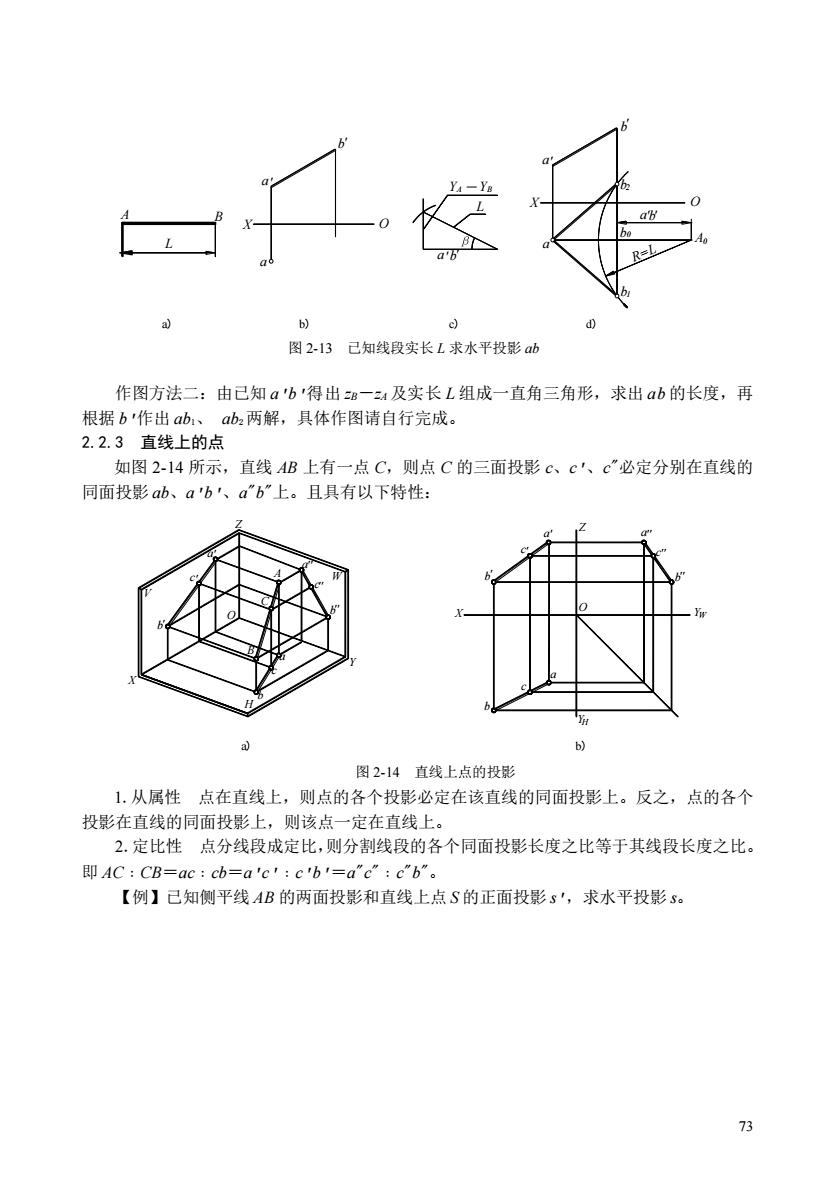
图2-13已知线段实长L求水平投影 作图方法二:由已知ab得出一4及实长L组成一直角三角形,求出ab的长度,再 根据b'作出ab、abz两解,具体作图请自行完成。 2.2.3直线上的点 如图2-14所示,直线AB上有一点C,则点C的三面投影c、c'、c“必定分别在直线的 同面投影ab、ab'、a"b”上。且具有以下特性: 图2-14直线上点的投影 1.从属性点在直线上,则点的各个投影必定在该直线的同面投影上。反之,点的各个 投影在直线的同面投影上,则该点一定在直线上。 2.定比性点分线段成定比,则分割线段的各个同面投影长度之比等于其线段长度之比。 即AC:CB=ac:ch=a'c':c'b'=a"c":c"b"。 【例】已知侧平线AB的两面投影和直线上点S的正面投影s',求水平投影s 73
73 作图方法二:由已知 a'b'得出 zB-zA 及实长 L 组成一直角三角形,求出 ab 的长度,再 根据 b'作出 ab1、 ab2 两解,具体作图请自行完成。 2.2.3 直线上的点 如图 2-14 所示,直线 AB 上有一点 C,则点 C 的三面投影 c、c'、c"必定分别在直线的 同面投影 ab、a'b'、a"b"上。且具有以下特性: 1.从属性 点在直线上,则点的各个投影必定在该直线的同面投影上。反之,点的各个 投影在直线的同面投影上,则该点一定在直线上。 2.定比性 点分线段成定比,则分割线段的各个同面投影长度之比等于其线段长度之比。 即 AC﹕CB=ac﹕cb=a'c'﹕c'b'=a"c"﹕c"b"。 【例】已知侧平线 AB 的两面投影和直线上点 S 的正面投影 s',求水平投影 s。 A B X a a b X a a b A b b b 2 0 1 0 L ' ' ' ' R=L a'b' O O a'b' L YA YB a) b) c) d) 图 2-13 已知线段实长 L 求水平投影 ab X Z Y a a a O Z X YW a a a O A B b b b b b b c c c c c c YH ' ' ' '' '' '' ' ' ' '' '' '' C V H W a) b) 图 2-14 直线上点的投影
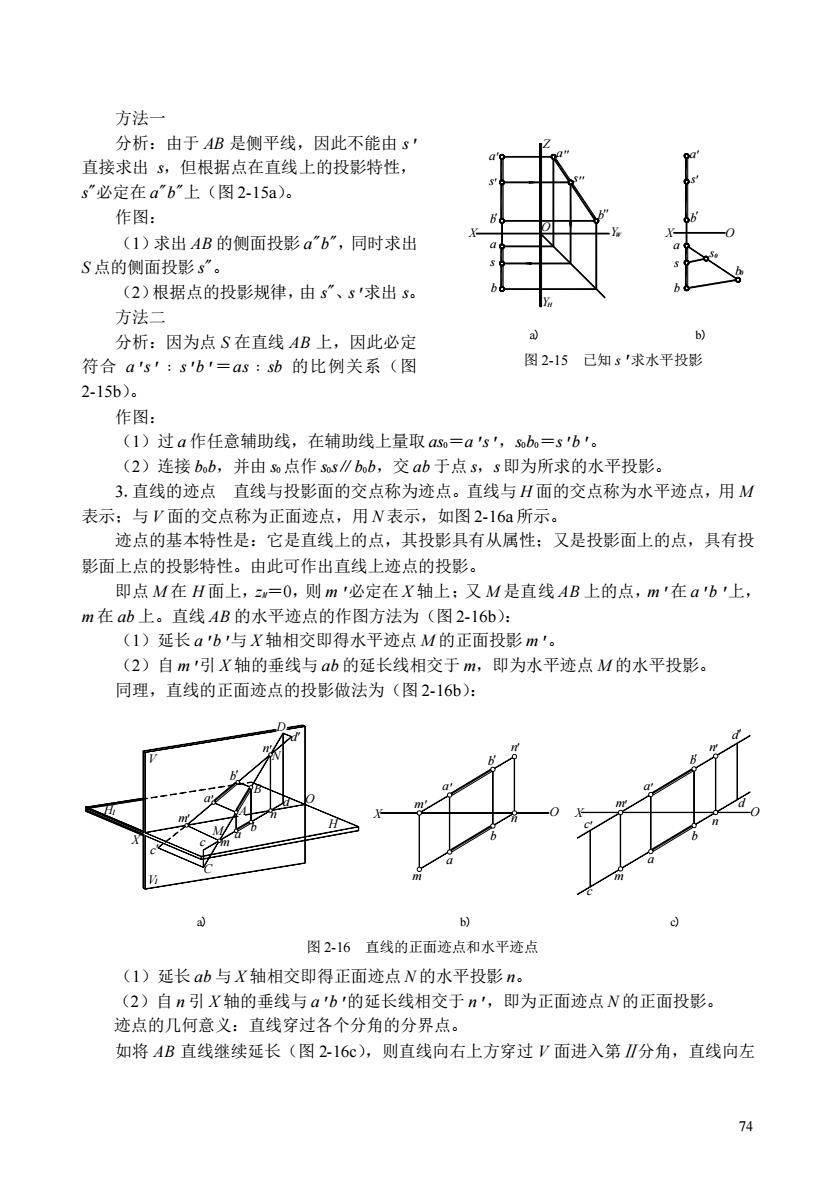
方法一 分析:由于AB是侧平线,因此不能由s 直接求出S,但根据点在直线上的投影特性, s”必定在ab”上(图2-15a) 作图: (1)求出AB的侧面投影a“b”,同时求出 S点的侧面投影s”。 (2)根据点的投影规律,由s”、s'求出s。 方法二 分析:因为点S在直线AB上,因此必定 符合a's':sb'=as:sb的比例关系(图 图215己知s'求水平投影 2-15b)。 作图: (1)过a作任意辅助线,在辅助线上量取a=a's',sb,=sb'。 (2)连接bb,并由s0点作ss∥bb,交ab于点s,s即为所求的水平投影。 3.直线的迹点直线与投影面的交点称为迹点。直线与H面的交点称为水平迹点,用M 表示:与V面的交点称为正面迹点,用N表示,如图216a所示。 迹点的基本特性是:它是直线上的点,其投影具有从属性:又是投影面上的点,具有投 影面上点的投影特性。由此可作出直线上迹点的投影。 即点M在H面上,=0,则m'必定在X轴上:又M是直线AB上的点,m'在ab上, m在ab上。直线AB的水平迹点的作图方法为(图2-16b): (1)延长ab与X轴相交即得水平迹点M的正面投影m。 (2)自m'引X轴的垂线与b的延长线相交于m,即为水平迹点M的水平投影。 同理,直线的正面迹点的投影做法为(图2-16b): 图2-16直线的正面迹点和水平迹点 (1)延长ab与X轴相交即得正面迹点N的水平投影n。 (2)自n引X轴的垂线与ab的延长线相交于n',即为正面迹点N的正面投影。 迹点的几何意义:直线穿过各个分角的分界点。 如将AB直线继续延长(图216c),则直线向右上方穿过V面进入第Ⅱ分角,直线向左 74
74 方法一 分析:由于 AB 是侧平线,因此不能由 s' 直接求出 s,但根据点在直线上的投影特性, s"必定在 a"b"上(图 2-15a)。 作图: (1)求出 AB 的侧面投影 a"b",同时求出 S 点的侧面投影 s"。 (2)根据点的投影规律,由 s"、s'求出 s。 方法二 分析:因为点 S 在直线 AB 上,因此必定 符合 a's'﹕s'b'=as﹕sb 的比例关系(图 2-15b)。 作图: (1)过 a 作任意辅助线,在辅助线上量取 as0=a's',s0b0=s'b'。 (2)连接 b0b,并由 s0 点作 s0s∥b0b,交 ab 于点 s,s 即为所求的水平投影。 3.直线的迹点 直线与投影面的交点称为迹点。直线与 H 面的交点称为水平迹点,用 M 表示;与 V 面的交点称为正面迹点,用 N 表示,如图 2-16a 所示。 迹点的基本特性是:它是直线上的点,其投影具有从属性;又是投影面上的点,具有投 影面上点的投影特性。由此可作出直线上迹点的投影。 即点 M 在 H 面上,zM=0,则 m'必定在 X 轴上;又 M 是直线 AB 上的点,m'在 a'b'上, m 在 ab 上。直线 AB 的水平迹点的作图方法为(图 2-16b): (1)延长 a'b'与 X 轴相交即得水平迹点 M 的正面投影 m'。 (2)自 m'引 X 轴的垂线与 ab 的延长线相交于 m,即为水平迹点 M 的水平投影。 同理,直线的正面迹点的投影做法为(图 2-16b): (1)延长 ab 与 X 轴相交即得正面迹点 N 的水平投影 n。 (2)自 n 引 X 轴的垂线与 a'b'的延长线相交于 n',即为正面迹点 N 的正面投影。 迹点的几何意义:直线穿过各个分角的分界点。 如将 AB 直线继续延长(图 2-16c),则直线向右上方穿过 V 面进入第Ⅱ分角,直线向左 Z X Y Y O X a s b a s b a s b a s b a s b s b H W 0 0 ' ' ' '' '' '' ' ' ' O a) b) 图 2-15 已知 s'求水平投影 X m a m a b n b n X c c m a m a b n b n d d c C c m a b n d m a b n d M A B N D ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' O O X O H V V H 1 1 a) b) c) 图 2-16 直线的正面迹点和水平迹点

下方向穿过H面进入第W分角,因此直线穿过、I、三个分角,即DN在第I分角,MN 在第I分角,MC在第W分角。 2.2.4两直线的相对位置 空间两直线的相对位置有三种情况:即两直线平行,两直线相交和两直线交叉。前两种 情况两直线位于同一平面上,称为同面直线:后一种情况两直线不位于同一平面上,称为异 面直线。 1.平行两直线空间两平行直线的同面投影必定互相平行,如图2-17a所示。由于AB CD,则有ab∥cd,ab'∥c'd',a"b"∥c"r。 反之,如果两直线同面投影都互相平行,则两直线在空间必定互相平行。 图2-17平行两直线的投影 【例】判别图2-18a所示的两侧平线是否平行(不利用侧面投影)。 图2-18b根据平行直线投影的等比关系作图。 图2-18c根据平行两直线、相交两直线为同面直线的性质作图。 图218判别两侧平线的相对位置 2.相交两直线空间两相交直线的投影必定相交,且两直线交点的投影一定为两直线投 影的交点,如图2-19a所示。AB与CD相交,交点为K,则ab与cd、a'b与c'd'、a”b"与 c"d必定分别相交于k、k'、k
75 下方向穿过 H 面进入第Ⅳ分角,因此直线穿过Ⅱ、Ⅰ、Ⅳ三个分角,即 DN 在第Ⅱ分角,MN 在第Ⅰ分角,MC 在第Ⅳ分角。 2.2.4 两直线的相对位置 空间两直线的相对位置有三种情况:即两直线平行,两直线相交和两直线交叉。前两种 情况两直线位于同一平面上,称为同面直线;后一种情况两直线不位于同一平面上,称为异 面直线。 1.平行两直线 空间两平行直线的同面投影必定互相平行,如图 2-17a 所示。由于 AB∥ CD,则有 ab∥cd,a'b'∥c'd',a"b"∥c"d"。 反之,如果两直线同面投影都互相平行,则两直线在空间必定互相平行。 【例】判别图 2-18a 所示的两侧平线是否平行(不利用侧面投影)。 图 2-18b 根据平行直线投影的等比关系作图。 图 2-18c 根据平行两直线、相交两直线为同面直线的性质作图。 2.相交两直线 空间两相交直线的投影必定相交,且两直线交点的投影一定为两直线投 影的交点,如图 2-19a 所示。AB 与 CD 相交,交点为 K,则 ab 与 cd、a 'b '与 c 'd '、a"b"与 c"d"必定分别相交于 k、k '、k"。 A B C D a b c d c c a X b d a d b O c YH YW d a b Z ' ' '' '' '' '' ' ' H a) b) 图 2-17 平行两直线的投影 a b c d c d a b X k k X b a b a d c d c s b0 X s b 0 a s b a d c d c ' ' ' ' ' ' ' ' ' ' ' ' ' ' O O O a) b) c) 图 2-18 判别两侧平线的相对位置
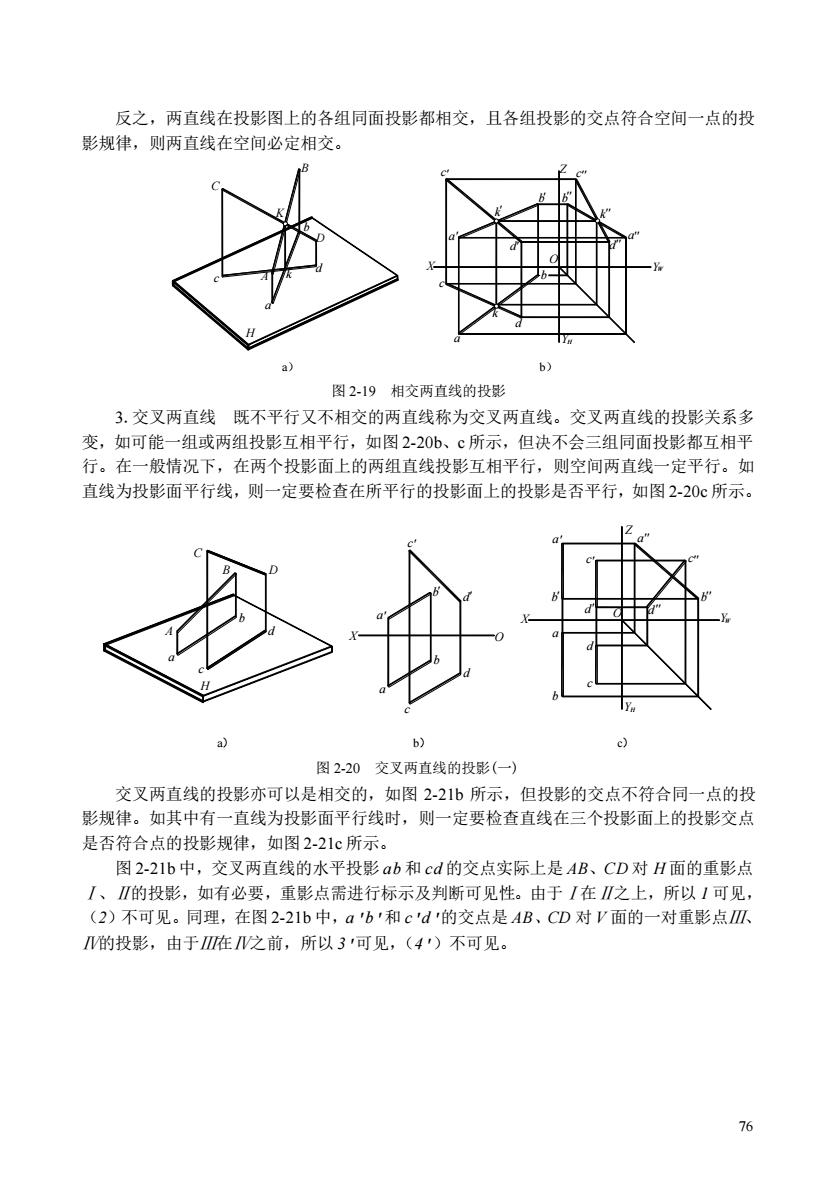
反之,两直线在投影图上的各组同面投影都相交,且各组投影的交点符合空间一点的投 影规律,则两直线在空间必定相交。 6 图2-19相交两直线的投影 3.交叉两直线既不平行又不相交的两直线称为交叉两直线。交叉两直线的投影关系多 变,如可能一组或两组投影互相平行,如图2-20b、c所示,但决不会三组同面投影都互相平 行。在一般情况下,在两个投影面上的两组直线投影互相平行,则空间两直线一定平行。如 直线为投影面平行线,则一定要检查在所平行的投影面上的投影是否平行,如图2-20c所示。 图2-20交叉两直线的投影(一) 交叉两直线的投影亦可以是相交的,如图22b所示,但投影的交点不符合同一点的投 影规律。如其中有一直线为投影面平行线时,则一定要检查直线在三个投影面上的投影交点 是否符合点的投影规律,如图2-21c所示。 图2-21b中,交叉两直线的水平投影ab和cd的交点实际上是AB、CD对H面的重影点 I、的投影,如有必要,重影点需进行标示及判断可见性。由于/在∥之上,所以1可见 (2)不可见。同理,在图2-21b中,ab'和c'd的交点是AB、CD对V面的一对重影点瓜 的投影,由于在之前,所以3可见,(4)不可见。 76
76 反之,两直线在投影图上的各组同面投影都相交,且各组投影的交点符合空间一点的投 影规律,则两直线在空间必定相交。 3.交叉两直线 既不平行又不相交的两直线称为交叉两直线。交叉两直线的投影关系多 变,如可能一组或两组投影互相平行,如图 2-20b、c 所示,但决不会三组同面投影都互相平 行。在一般情况下,在两个投影面上的两组直线投影互相平行,则空间两直线一定平行。如 直线为投影面平行线,则一定要检查在所平行的投影面上的投影是否平行,如图 2-20c 所示。 交叉两直线的投影亦可以是相交的,如图 2-21b 所示,但投影的交点不符合同一点的投 影规律。如其中有一直线为投影面平行线时,则一定要检查直线在三个投影面上的投影交点 是否符合点的投影规律,如图 2-21c 所示。 图 2-21b 中,交叉两直线的水平投影 ab 和 cd 的交点实际上是 AB、CD 对 H 面的重影点 Ⅰ、Ⅱ的投影,如有必要,重影点需进行标示及判断可见性。由于Ⅰ在Ⅱ之上,所以 1 可见, (2)不可见。同理,在图 2-21b 中,a'b'和 c'd'的交点是 AB、CD 对 V 面的一对重影点Ⅲ、 Ⅳ的投影,由于Ⅲ在Ⅳ之前,所以 3'可见,(4')不可见。 Z X Y Y O a a c c b d b d a c H W b d k k k c C b a A k d K B D ' '' '' '' '' ' '' ' ' ' H a) b) 图 2-19 相交两直线的投影 X c d b a a b c d A a c b B C d D Y O X b a c d a b d c Y H W d c a Z b ' ' ' ' ' ' ' ' '' '' '' '' O H a) b) c) 图 2-20 交叉两直线的投影(一)
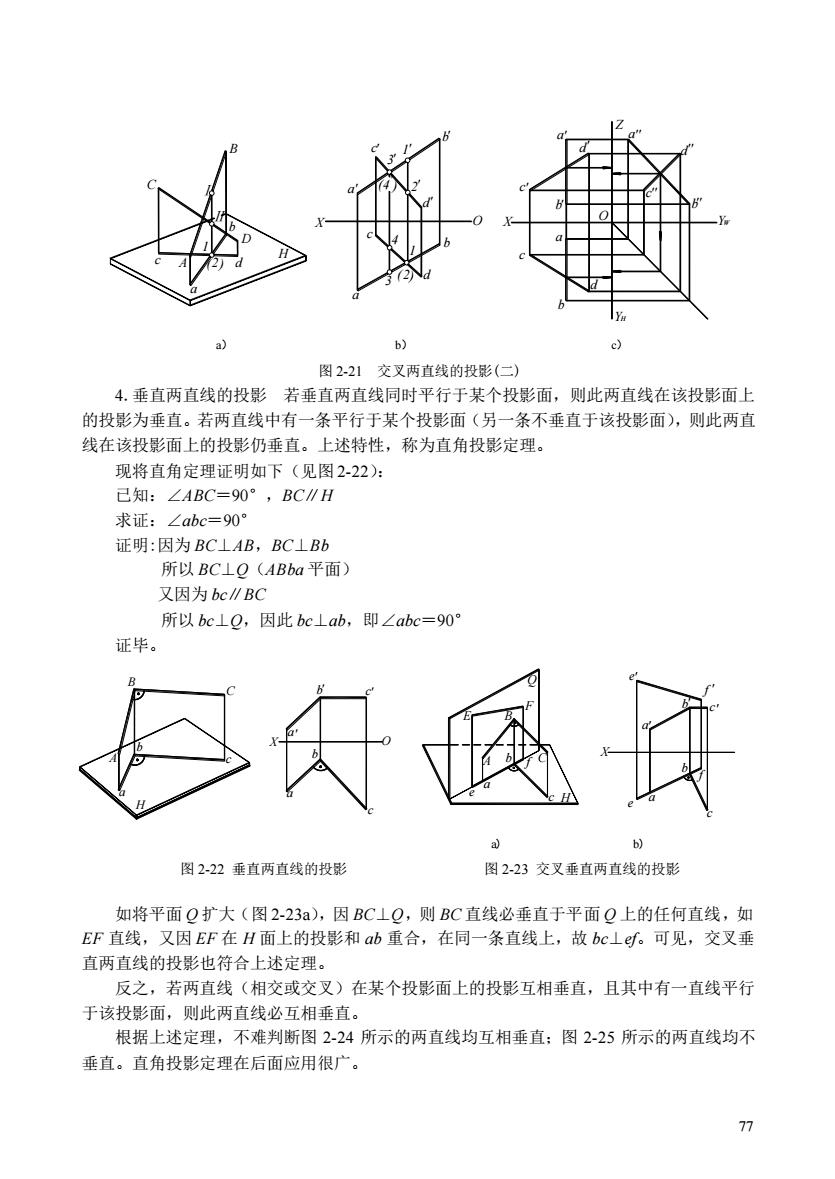
图2-21交叉两直线的投影(二) 4.垂直两直线的投影若垂直两直线同时平行于某个投影面,则此两直线在该投影面上 的投影为垂直。若两直线中有一条平行于某个投影面(另一条不垂直于该投影面),则此两直 线在该投影面上的投影仍垂直。上述特性,称为直角投影定理。 现将直角定理证明如下(见图2-22): 己知:∠ABC=90°,BC∥H 求证:∠abc=90° 证明:因为BC⊥AB,BC⊥Bb 所以BC⊥Q(ABba平面) 又因为bc∥BC 所以bc⊥Q,因此bc⊥ab,即∠abc=90 证毕。 b) 图2-22垂直两直线的投影 图2-23交叉垂直两直线的投影 如将平面Q扩大(图2-23a),因BC⊥Q,则BC直线必垂直于平面Q上的任何直线,如 EF直线,又因EF在H面上的投影和ab重合,在同一条直线上,故bc⊥e。可见,交叉垂 直两直线的投影也符合上述定理。 反之,若两直线(相交或交叉)在某个投影面上的投影互相垂直,且其中有一直线平行 于该投影面,则此两直线必互相垂直。 根据上述定理,不难判断图2-24所示的两直线均互相垂直:图2-25所示的两直线均不 垂直。直角投影定理在后面应用很广。 77
77 4.垂直两直线的投影 若垂直两直线同时平行于某个投影面,则此两直线在该投影面上 的投影为垂直。若两直线中有一条平行于某个投影面(另一条不垂直于该投影面),则此两直 线在该投影面上的投影仍垂直。上述特性,称为直角投影定理。 现将直角定理证明如下(见图 2-22): 已知:∠ABC=90°,BC∥H 求证:∠abc=90° 证明:因为 BC⊥AB,BC⊥Bb 所以 BC⊥Q(ABba 平面) 又因为 bc∥BC 所以 bc⊥Q,因此 bc⊥ab,即∠abc=90° 证毕。 如将平面 Q 扩大(图 2-23a),因 BC⊥Q,则 BC 直线必垂直于平面 Q 上的任何直线,如 EF 直线,又因 EF 在 H 面上的投影和 ab 重合,在同一条直线上,故 bc⊥ef。可见,交叉垂 直两直线的投影也符合上述定理。 反之,若两直线(相交或交叉)在某个投影面上的投影互相垂直,且其中有一直线平行 于该投影面,则此两直线必互相垂直。 根据上述定理,不难判断图 2-24 所示的两直线均互相垂直;图 2-25 所示的两直线均不 垂直。直角投影定理在后面应用很广。 X c d b a a b c d 1 2 3 4 1 2 3 4 a c b A C B D d Y O X c d b a c b a d Y H W d c a Z b ' ' ' ' ' ' ' ' ' ' ' ' '' '' '' '' ( ) ( ) 1 (2) Ⅰ Ⅱ O H a) b) c) 图 2-21 交叉两直线的投影(二) A B C a b c a b c b c a X ' ' ' O H 图4-23 Q X ' ' ' ' ' c e f b a c b a f e c b a f e H C F E B A a) b) 图 2-22 垂直两直线的投影 图 2-23 交叉垂直两直线的投影