其中xc=D,℃=D,因此,它们的正面投影c'和(d)重影为一点,由于℃>o,所以从 前向后看时,C是可见的,D是不可见的。通常规定把不可见的点的投影加上括号,如(d) 以示区别。又如C、E两点,其中xC=,比=,因此它们的水平投影(c)、e重影为一点, 由于,E>C,所以从上面垂直H面向下看时E是可见的,C是不可见的。再如C、F两点 其中C=r,C=r,它们的侧面投影c”、(f门重影为一点,由于xC>x,所以从左面垂直 于W面向右看时,C是可见的,F是不可见的。由此可见,对V面、H面、W面的重影点 它们的可见性,应分别是前遮后、上遮下、左遮右。此外,一个点在一个方向上是可见的, 在另一方向上去看则不一定是可见,必须根据该点和其他点的相对位置而定。 在投影图上,如果两个点的投影重合,则对重合投影所在投影面的距离(即对该投影面 的坐标值)较大的那个点是可见的,而另一个点是不可见的,因此经常利用重影点来判别可 见性问题。 图210重形点的投影 2.2直线的投影 空间一直线的投影可由直线的两点(通常取线段两个端点)的投影来确定。如图2-11所 示的直线AB,求作它的三面投影时,可分别作出两端点的投影(a、a'、a”)、(b、b'、b"), 然后将其同面投影连接起来即得直线的三面投影(ab、ab,、ab“)。 68
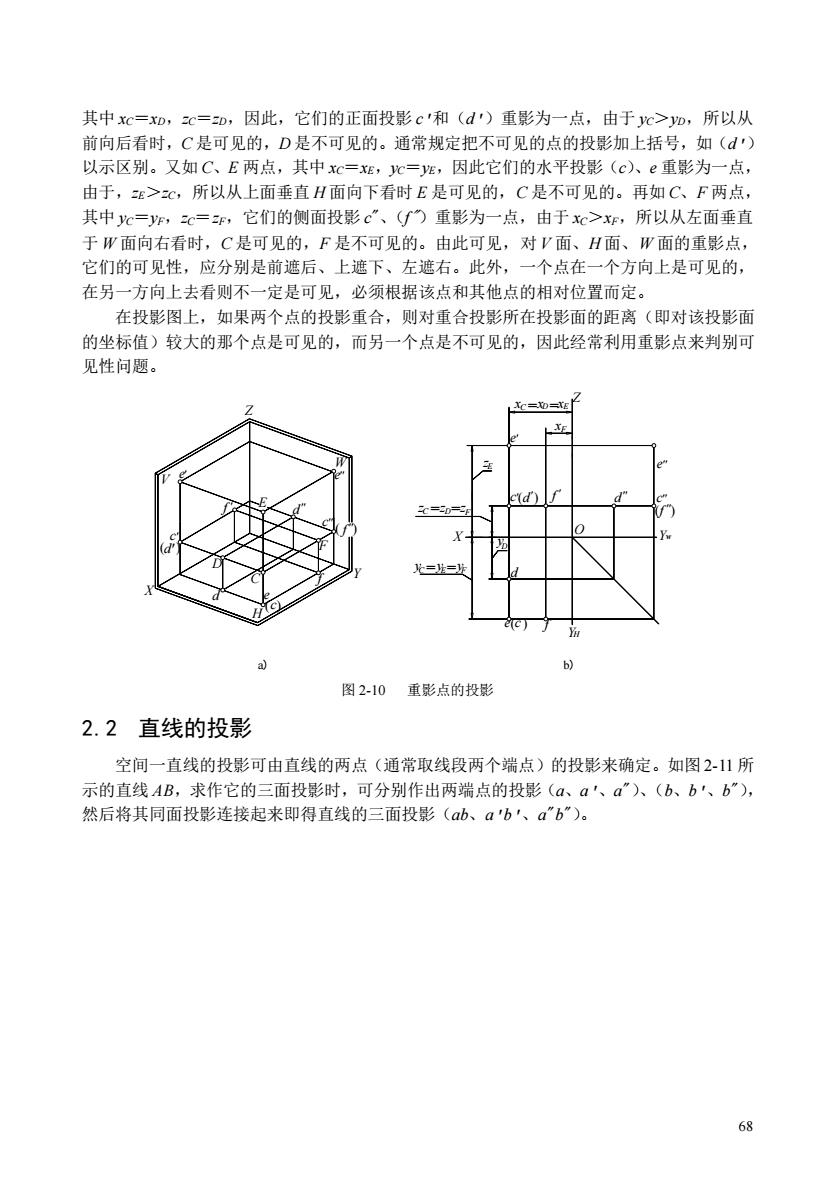
68 其中 xC=xD,zC=zD,因此,它们的正面投影 c'和(d')重影为一点,由于 yC>yD,所以从 前向后看时,C 是可见的,D 是不可见的。通常规定把不可见的点的投影加上括号,如(d') 以示区别。又如 C、E 两点,其中 xC=xE,yC=yE,因此它们的水平投影(c)、e 重影为一点, 由于,zE>zC,所以从上面垂直 H 面向下看时 E 是可见的,C 是不可见的。再如 C、F 两点, 其中 yC=yF,zC=zF,它们的侧面投影 c"、(f")重影为一点,由于 xC>xF,所以从左面垂直 于 W 面向右看时,C 是可见的,F 是不可见的。由此可见,对 V 面、H 面、W 面的重影点, 它们的可见性,应分别是前遮后、上遮下、左遮右。此外,一个点在一个方向上是可见的, 在另一方向上去看则不一定是可见,必须根据该点和其他点的相对位置而定。 在投影图上,如果两个点的投影重合,则对重合投影所在投影面的距离(即对该投影面 的坐标值)较大的那个点是可见的,而另一个点是不可见的,因此经常利用重影点来判别可 见性问题。 e' Z W H V c'' e( ) d ( ) ( ) '' '' '' '' ' ' ' O c f f c e c d f d = = = = = = F F D D E C E C y y y y z z z z x x x F xC D E ) ) ) ( ( ( '' '' '' ' ' ' ' d f f f c d d c D C F e e E e YH X Yw Z Y X a) b) 图 2-10 重影点的投影 2.2 直线的投影 空间一直线的投影可由直线的两点(通常取线段两个端点)的投影来确定。如图 2-11 所 示的直线 AB,求作它的三面投影时,可分别作出两端点的投影(a、a'、a")、(b、b'、b"), 然后将其同面投影连接起来即得直线的三面投影(ab、a'b'、a"b")
40 图2.11直线的投影 图2-1ld为直线AB的投影在画物体投影图中的应用。 2.2.1各种位置直线的投影特性 根据直线在三投影面体系中的位置可将其分为投影面倾斜线、投影面平行线和投影面垂 直线三类。 前一类直线称为一般位置直线,后两类直线称为特殊位置直线。它们具有不同的投影特 性,现分述如下: 1.投影面倾斜线与三个投影面都成倾斜的直线称为投影面倾斜线。如图211所示,设 倾斜线AB对H面的倾角为a,对面的倾角为B,对W面的倾角为Y,则直线的实长、投 影长度和倾角之间的关系为: ab=ABcos a: a'b=ABcos B: ab=ABcos y 由上式可知,当直线处于倾斜位置时,由于0<a<90°:0<B<90°;0<y<90°, 因此直线的三个投影均小于实长。 倾斜线的投影特性为:三个投影都与投影轴倾斜且都小于实长。各个投影与投影轴的夹 角都不反映直线对投影面的夹角。 2.投影面平行线平行于一个投影面而与另外两个投影面倾斜的直线称为投影面平行 线。如表2-1所示,平行V面的称为正平线:平行H面的直线称为水平线:平行于W面的称 为侧平线。 以正平线AB为例,其投影特性为: (1)正面投影ab'反映直线的实长,它与X轴的夹角反映直线对H面的倾角,与Z轴 69
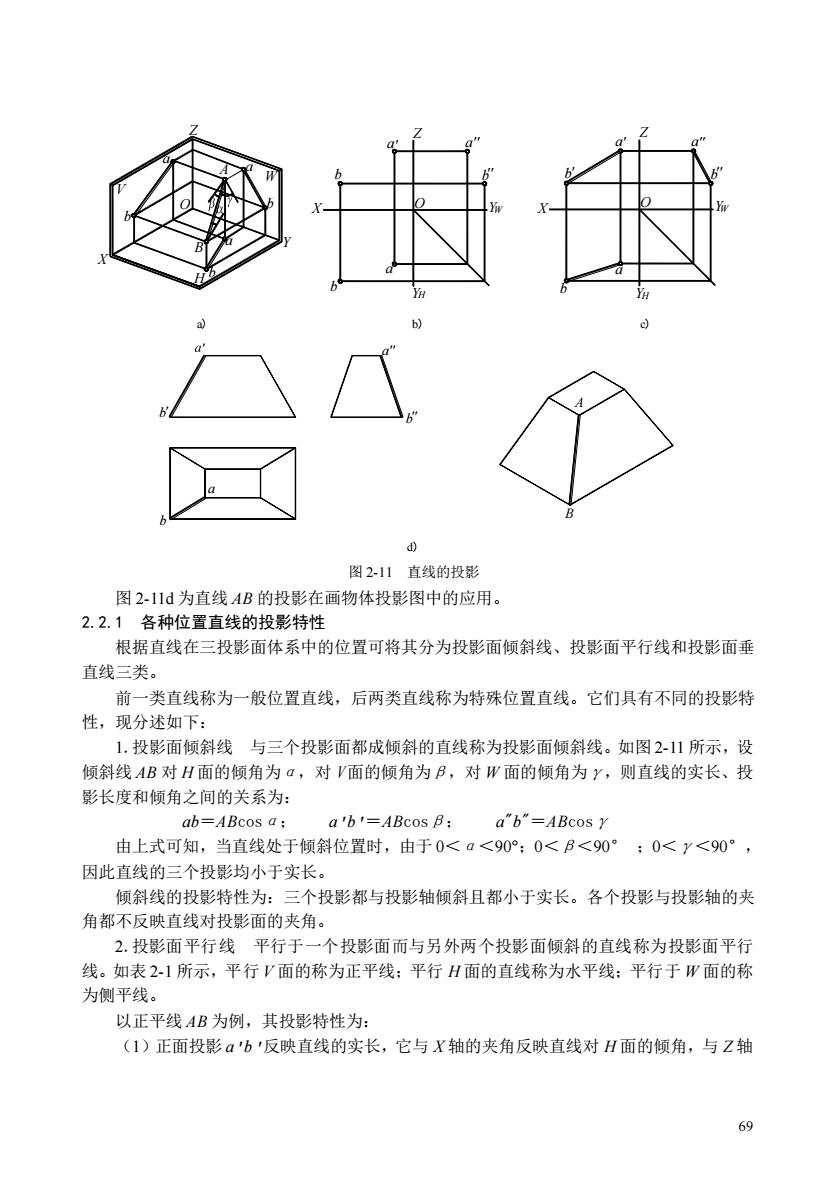
69 图 2-11d 为直线 AB 的投影在画物体投影图中的应用。 2.2.1 各种位置直线的投影特性 根据直线在三投影面体系中的位置可将其分为投影面倾斜线、投影面平行线和投影面垂 直线三类。 前一类直线称为一般位置直线,后两类直线称为特殊位置直线。它们具有不同的投影特 性,现分述如下: 1.投影面倾斜线 与三个投影面都成倾斜的直线称为投影面倾斜线。如图 2-11 所示,设 倾斜线 AB 对 H 面的倾角为α,对 V 面的倾角为β,对 W 面的倾角为γ,则直线的实长、投 影长度和倾角之间的关系为: ab=ABcosα; a'b'=ABcosβ; a"b"=ABcosγ 由上式可知,当直线处于倾斜位置时,由于 0<α<90°;0<β<90° ;0<γ<90°, 因此直线的三个投影均小于实长。 倾斜线的投影特性为:三个投影都与投影轴倾斜且都小于实长。各个投影与投影轴的夹 角都不反映直线对投影面的夹角。 2.投影面平行线 平行于一个投影面而与另外两个投影面倾斜的直线称为投影面平行 线。如表 2-1 所示,平行 V 面的称为正平线;平行 H 面的直线称为水平线;平行于 W 面的称 为侧平线。 以正平线 AB 为例,其投影特性为: (1)正面投影 a'b'反映直线的实长,它与 X 轴的夹角反映直线对 H 面的倾角,与 Z 轴 X Z Y a a a O Z X YW YH a a a O A B b b b b b b Z O H X Y b a b a YW a b ' '' '' ' ' '' '' V H W a) b) c) ' b' a'' b'' a b A B d) 图 2-11 直线的投影
的夹角反映直线对W面的倾角。 (2)水平投影ab∥X轴:侧面投影ab∥Z轴,它们的投影长度均小于AB实长 ab=ABcos a,a"b"=ABcos y 关于水平线和侧平线投影其投影特性可类似得出 表21平行线的投影特性 正平线(AB∥V面) 水平线(AB∥H而) 侧平线(AB∥W面) 图 图 1.abM=AB:r面投影反映a 的BH面投影反映、了 1.ab诗=AB:V面投影反映a 2.a∥oZ、abM<4B, ab∥OYH、ab<AB 3.投影面垂直线垂直于一个投影面即与另外两个投影面都平行的直线称为投影面垂 直线(表2-2)。垂直于正面的称为正垂线:垂直于水平面称为铅垂线,垂直于侧面的称为侧 垂线。 70
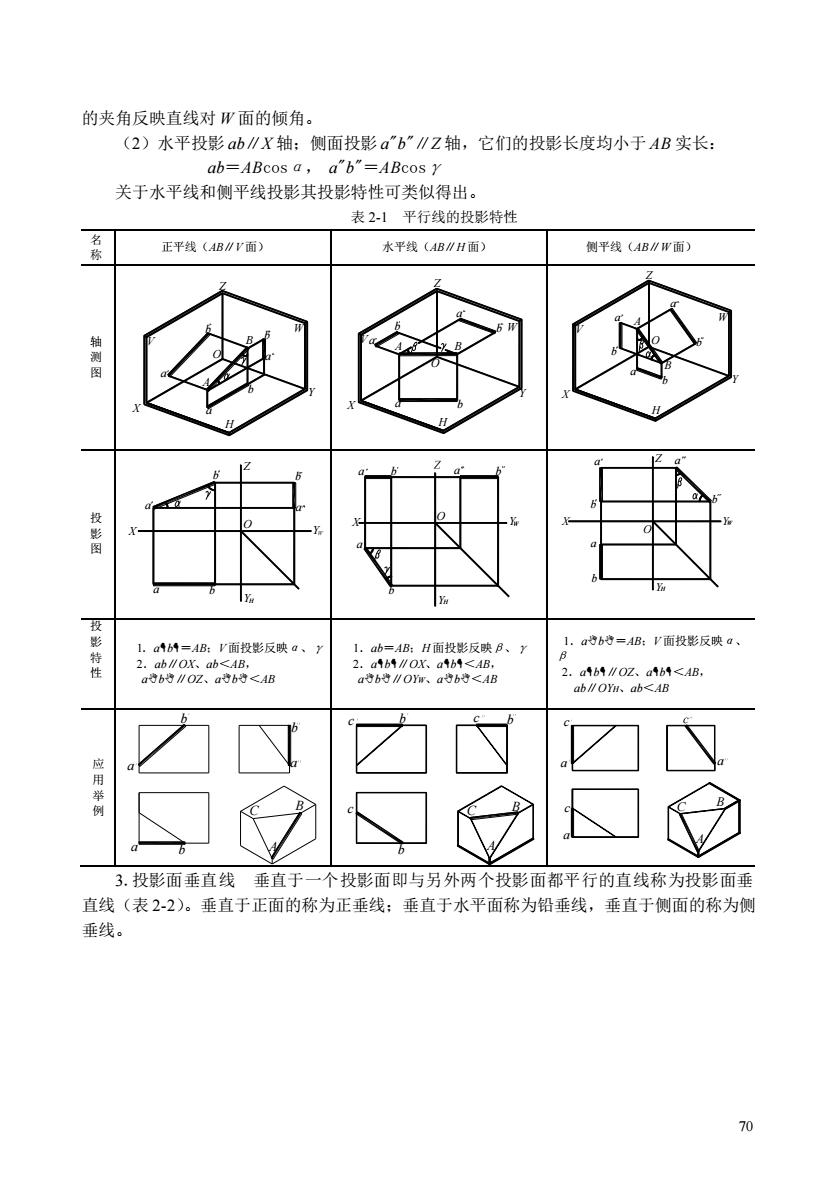
70 的夹角反映直线对 W 面的倾角。 (2)水平投影 ab∥X 轴;侧面投影 a"b"∥Z 轴,它们的投影长度均小于 AB 实长: ab=ABcosα, a"b"=ABcosγ 关于水平线和侧平线投影其投影特性可类似得出。 表 2-1 平行线的投影特性 名 称 正平线(AB∥V 面) 水平线(AB∥H 面) 侧平线(AB∥W 面) 轴 测 图 X Z Y a b A B b a a b O V H W X Z Y a b A B a a b b H W V O X Z Y a b a b a b A B W H V O 投 影 图 X a b Y YH a O Z b a b X a b a b YW YH O a b O X a b b a YW YH Z a b 投 影 特 性 1.ab=AB;V 面投影反映α、γ 2.ab∥OX、ab<AB, ab∥OZ、ab<AB 1.ab=AB;H 面投影反映β、γ 2.ab∥OX、ab<AB, ab∥OYW、ab<AB 1.ab=AB;V 面投影反映α、 β 2.ab∥OZ、ab<AB, ab∥OYH、ab<AB 应 用 举 例 a a b b a b A B C c c b b c b A C B a a c c a A B C 3.投影面垂直线 垂直于一个投影面即与另外两个投影面都平行的直线称为投影面垂 直线(表 2-2)。垂直于正面的称为正垂线;垂直于水平面称为铅垂线,垂直于侧面的称为侧 垂线

表22垂直线的投影特性 正线(4B1r面) 铅垂线(4BLH面) 侧垂线(4B⊥W面) 轴测图 器 1.a3(b的)积聚成一点 以铅垂线为例,其投影特性为: (1)水平投影a(b)重影为一点。 (2)正面投影a'b垂直X轴:侧面投影a“b“垂直Y,轴,均反映实长。 关于正垂线和侧垂线的投影及其投影特性可类似得出。 2.2.2直线段的实长和对投影红面的顷角 由前述得知,倾斜直线段的投影在投影图上不反映实长和对投影面的倾角。但在工程上 往往要求在投影图上用图解方法解决这一度量问题
71 表 2-2 垂直线的投影特性 名 称 正垂线(AB⊥V 面) 铅垂线(AB⊥H 面) 侧垂线(AB⊥W 面) 轴 测 图 A B X Y Z a b a b a b O V H W a b b a A B Z Y X a b O W H V A B X Y a b a b a b O W H V 投 影 图 O X b a a b YW YH b Z a O X YW YH a Z b a b a b X a b a b YW YH b O a Z 投 影 特 性 1.a(b)积聚成一点 2.ab⊥OX、ab⊥OZ 3.ab=ab=AB 1.a(b)积聚成一点 2.ab⊥OX、ab⊥OYW 3.ab=ab=AB 1.a(b)积聚成一点 2.ab⊥OZ、ab⊥OYH 3.ab=ab=AB 应 用 举 例 a a b b a b A B C D a a d d a d D B C A a c a c a c B D C A 以铅垂线为例,其投影特性为: (1)水平投影 a(b)重影为一点。 (2)正面投影 a'b'垂直 X 轴;侧面投影 a"b"垂直 YW轴,均反映实长。 关于正垂线和侧垂线的投影及其投影特性可类似得出。 2.2.2 直线段的实长和对投影面的倾角 由前述得知,倾斜直线段的投影在投影图上不反映实长和对投影面的倾角。但在工程上, 往往要求在投影图上用图解方法解决这一度量问题
1.几何分析如图2-12所示为一处于H/N投影面体系中的倾斜线AB,现过A作AB,∥ ab,即得一直角三角形ABB,它的斜边AB即为其实长,AB:=b,BB:为两端点A、B的: 图212直角三角形法求实长及顿角 坐标差(B一:4),AB与AB的夹角即为AB对H面的倾角a。由此可见,根据倾斜线AB的 投影,求实长和对H面的倾角,可归结为求直角三角形ABB的实形。 如过A作AB:∥ab',则得另一直角三角形ABB2,它的斜边AB即为实长,AB2=a'b', BB:为两端点A、B的y坐标差(y一),AB与AB:的夹角即为AB对V面的倾角B。因此 只要求出直角三角形ABB:的实形,即可得到AB的实长和对投影面的倾角B。 2.作图方法求直线AB的实长和对H面的倾角a可应用下列两种方式作图(图2-12b): (1)如图2-12所示,过b作ab的垂线bBo,在此垂线上量取bB。=一4,则aB即为 所求直线的实长,∠Boab即为a角。 (2)过a作X轴的平行线,与bb相交于bo(bbo=B一4),量取b4o=ab,则bA 也是所求直线的实长,∠b4,b即为a角。 同理,如图2-12c所示,以ab'直角边,以一以为另一直角边,也可求出AB的实长 (bA。=AB),而斜边bA与ab的夹角即为AB对V面的倾角B,类似做法,使aB。=ab, 则aB。=AB,∠aBa也反映B角。 直线对侧面的倾角y请自行求出。 3.应用作图举例如图2-13所示,已知直线AB的实长L和ab'及a,求水平投影ab 分析:如求出了ab长度,或增一的值,就可确定b。根据直角三角形法,可以分析 想象由己知的ab和实长L能组成一直角三角形,并画出该三角形(图2-13C),标记直角 边ab'和斜边L,然后分析αb'和L的夹角和另一直角边各表示什么,弄清后即可得到解 题思路。 作图方法一: (1)由b'点作X轴的垂线bb。 (2)由a点作X轴平行线与b'b相交于b,延长ab至Ao,使baA=ab'。 (3)以A。为圆心,实长L为半径画圆弧交bb于b1或b2,即可求出水平投影ab或ab 两解,如果取后面一解,则B点处于第Ⅱ分角。 72
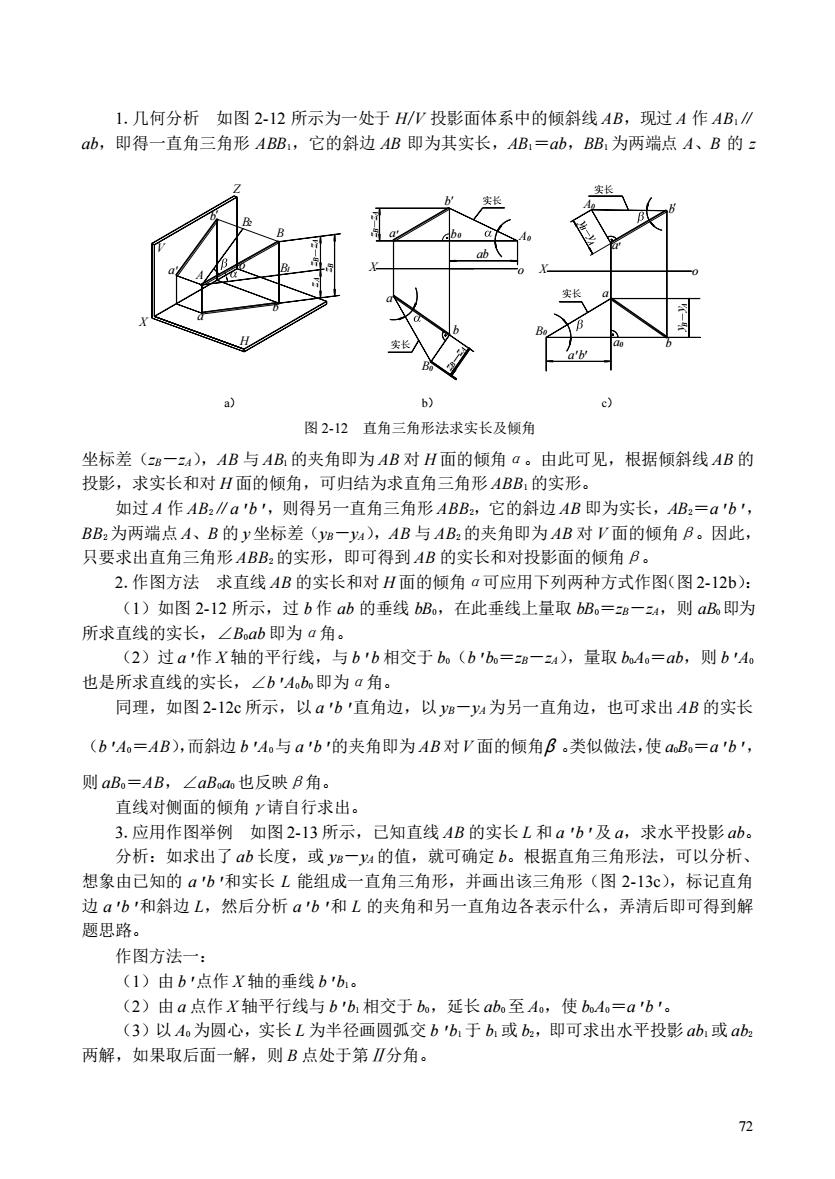
72 1.几何分析 如图 2-12 所示为一处于 H/V 投影面体系中的倾斜线 AB,现过 A 作 AB1∥ ab,即得一直角三角形 ABB1,它的斜边 AB 即为其实长,AB1=ab,BB1 为两端点 A、B 的 z 坐标差(zB-zA),AB 与 AB1 的夹角即为 AB 对 H 面的倾角α。由此可见,根据倾斜线 AB 的 投影,求实长和对 H 面的倾角,可归结为求直角三角形 ABB1 的实形。 如过 A 作 AB2∥a'b',则得另一直角三角形 ABB2,它的斜边 AB 即为实长,AB2=a'b', BB2 为两端点 A、B 的 y 坐标差(yB-yA),AB 与 AB2 的夹角即为 AB 对 V 面的倾角β。因此, 只要求出直角三角形 ABB2 的实形,即可得到 AB 的实长和对投影面的倾角β。 2.作图方法 求直线 AB 的实长和对 H 面的倾角α可应用下列两种方式作图(图 2-12b): (1)如图 2-12 所示,过 b 作 ab 的垂线 bB0,在此垂线上量取 bB0=zB-zA,则 aB0 即为 所求直线的实长,∠B0ab 即为α角。 (2)过 a'作 X 轴的平行线,与 b'b 相交于 b0(b'b0=zB-zA),量取 b0A0=ab,则 b'A0 也是所求直线的实长,∠b'A0b0 即为α角。 同理,如图 2-12c 所示,以 a'b'直角边,以 yB-yA 为另一直角边,也可求出 AB 的实长 (b'A0=AB),而斜边 b'A0与 a'b'的夹角即为 AB 对V 面的倾角β 。类似做法,使 a0B0=a'b', 则 aB0=AB,∠aB0a0 也反映β角。 直线对侧面的倾角γ请自行求出。 3.应用作图举例 如图 2-13 所示,已知直线 AB 的实长 L 和 a'b'及 a,求水平投影 ab。 分析:如求出了 ab 长度,或 yB-yA 的值,就可确定 b。根据直角三角形法,可以分析、 想象由已知的 a'b'和实长 L 能组成一直角三角形,并画出该三角形(图 2-13c),标记直角 边 a'b'和斜边 L,然后分析 a'b'和 L 的夹角和另一直角边各表示什么,弄清后即可得到解 题思路。 作图方法一: (1)由 b'点作 X 轴的垂线 b'b1。 (2)由 a 点作 X 轴平行线与 b'b1 相交于 b0,延长 ab0 至 A0,使 b0A0=a'b'。 (3)以 A0 为圆心,实长 L 为半径画圆弧交 b'b1 于 b1 或 b2,即可求出水平投影 ab1 或 ab2 两解,如果取后面一解,则 B 点处于第Ⅱ分角。 X Z a X a b b b a z A B X b a b a ' ' ' ' ' ' B a' b' z z z B A A B zB zA zB-zA 2 B1 A B b ab 0 0 0 0 实长 实长 a b a 实长 实长 y yA B yB yA A0 B0 o o o V H a) b) c) 图 2-12 直角三角形法求实长及倾角