
第5章曲线与曲面 曲线与曲面也是物体表面的重要组成部分。本章讨论常见的曲线、曲面的投影性质与作 图方法。 5.1曲线的形成与投影 1.曲线的形成与分类曲线可以看作为点连续运动的轨迹,也可认为是平面与曲面或两 曲面相交而成。 若曲线上所有的点属于同一平面,则此曲线称为平面曲线,如圆、椭圆、双曲线、抛物 线、渐伸线、摆线等。 若曲线上任意四个连续的点不属于同一平面,则此曲线称为空间曲线,如螺旋线等。 如图5-1所示,过曲线上点B作割线BD,当点D无限趋近于点B时,割线的极限位置 变为BN,即称BN为曲线在点B处的切线。对于平面曲线过切点且垂直于切线的直线,称为 过该点的法线。 图5-1空间曲线及其投影 图5-2不光滑空间曲线 如果曲线在其各点处都具有连续改变的切线,则称该曲线为光滑的曲线。 如图5-2所示的曲线就不是光滑的,因为在点B处切线不能连续变化。 可以用代数方程表示的曲线称为代数曲线。其代数方程的次数就是曲线的次数。对于平 面代数曲线的次数,可以用直线与该曲线最大可能交点数来确定。例如,二次曲线椭圆与直 线就有两个交点。 2.曲线投影的画法一般情况下,曲线至少需要两个投影才能确定出它在空间的形状和 位置。曲线的投影作图,就是按曲线形成的方法,依次画出曲线上一系列的点的各面投影, 然后把各点的同面投影顺次、光滑地连成曲线,这种作图方法称为坐标描点法。为了确保曲 线投影的准确和清晰,应优先选择一些具有关键位置的点,称为特殊点,如极限位置的点(最 高、最低、最前、最后、最左、最右诸点)以及如椭圆长短轴的端点等。 3.曲线投影的基本性质曲线的投影具有以下的性质,根据这些性质,在作曲线投影时, 可以保证投影的正确性和提高投影的准确性。 120
120 第 5 章 曲线与曲面 曲线与曲面也是物体表面的重要组成部分。本章讨论常见的曲线、曲面的投影性质与作 图方法。 5.1 曲线的形成与投影 1.曲线的形成与分类 曲线可以看作为点连续运动的轨迹,也可认为是平面与曲面或两 曲面相交而成。 若曲线上所有的点属于同一平面,则此曲线称为平面曲线,如圆、椭圆、双曲线、抛物 线、渐伸线、摆线等。 若曲线上任意四个连续的点不属于同一平面,则此曲线称为空间曲线,如螺旋线等。 如图 5-1 所示,过曲线上点 B 作割线 BD,当点 D 无限趋近于点 B 时,割线的极限位置 变为 BN,即称 BN 为曲线在点 B 处的切线。对于平面曲线过切点且垂直于切线的直线,称为 过该点的法线。 如果曲线在其各点处都具有连续改变的切线,则称该曲线为光滑的曲线。 如图 5-2 所示的曲线就不是光滑的,因为在点 B 处切线不能连续变化。 可以用代数方程表示的曲线称为代数曲线。其代数方程的次数就是曲线的次数。对于平 面代数曲线的次数,可以用直线与该曲线最大可能交点数来确定。例如,二次曲线椭圆与直 线就有两个交点。 2.曲线投影的画法 一般情况下,曲线至少需要两个投影才能确定出它在空间的形状和 位置。曲线的投影作图,就是按曲线形成的方法,依次画出曲线上一系列的点的各面投影, 然后把各点的同面投影顺次、光滑地连成曲线,这种作图方法称为坐标描点法。为了确保曲 线投影的准确和清晰,应优先选择一些具有关键位置的点,称为特殊点,如极限位置的点(最 高、最低、最前、最后、最左、最右诸点)以及如椭圆长短轴的端点等。 3.曲线投影的基本性质 曲线的投影具有以下的性质,根据这些性质,在作曲线投影时, 可以保证投影的正确性和提高投影的准确性。 N C D A B a b c d n H A B E a e b F C f c 图 5-1 空间曲线及其投影 图 5-2 不光滑空间曲线
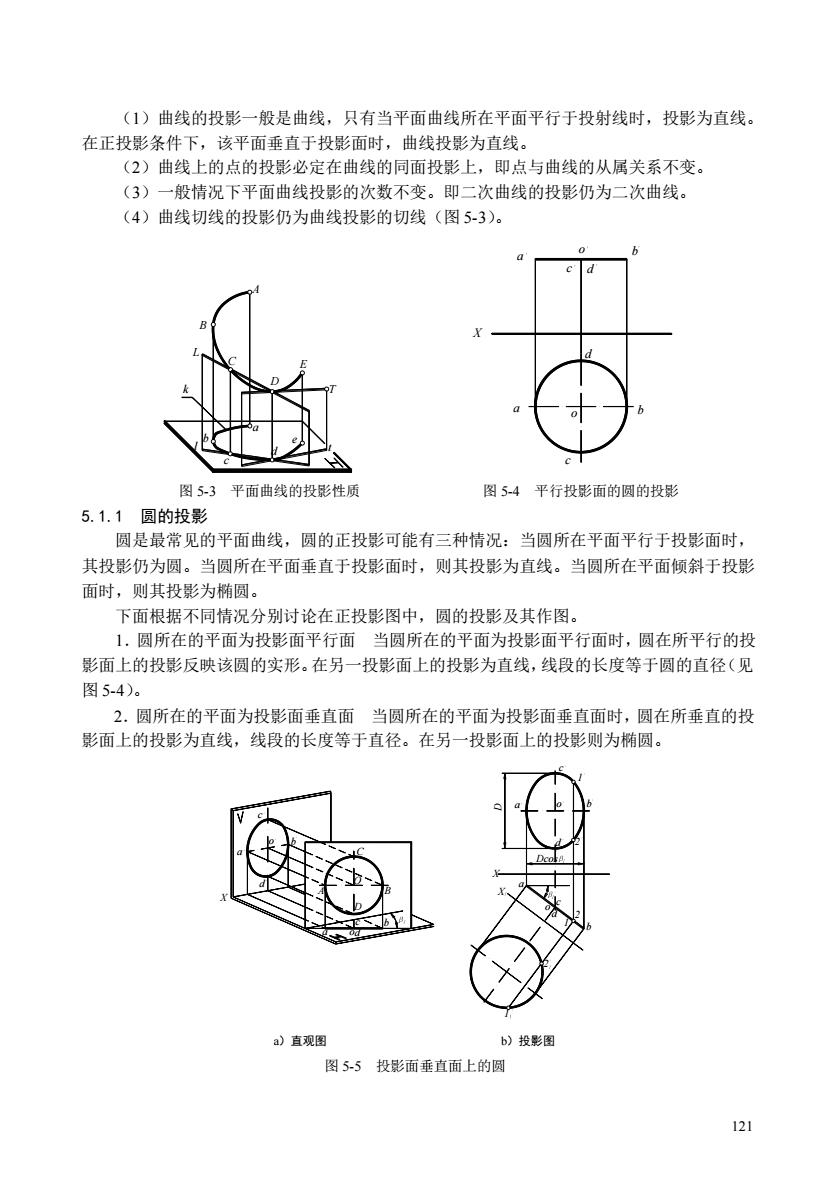
(1)曲线的投影一般是曲线,只有当平面曲线所在平面平行于投射线时,投影为直线。 在正投影条件下,该平面垂直于投影面时,曲线投影为直线。 (2)曲线上的点的投影必定在曲线的同面投影上,即点与曲线的从属关系不变, (3)一般情况下平面曲线投影的次数不变。即二次曲线的投影仍为二次曲线。 (4)曲线切线的投影仍为曲线投影的切线(图5-3)。 图53平面曲线的投形性质 图54平行投影面的圆的投影 5.1.1圆的投影 圆是最常见的平面曲线,圆的正投影可能有三种情况:当圆所在平面平行于投影面时, 其投影仍为圆。当圆所在平面垂直于投影面时,则其投影为直线。当圆所在平面倾斜于投影 面时,则其投影为椭圆。 下面根据不同情况分别讨论在正投影图中,圆的投影及其作图。 1,圆所在的平面为投影面平行面当圆所在的平面为投影面平行面时,圆在所平行的投 影面上的投影反映该圆的实形。在另一投影面上的投影为直线,线段的长度等于圆的直径(见 图5-4)。 2.圆所在的平面为投影面垂直面当圆所在的平面为投影面垂直面时,圆在所垂直的投 影面上的投影为直线,线段的长度等于直径。在另一投影面上的投影则为椭圆。 )直观图 b)投影图 图5-5投影面垂直面上的圆 121
121 (1)曲线的投影一般是曲线,只有当平面曲线所在平面平行于投射线时,投影为直线。 在正投影条件下,该平面垂直于投影面时,曲线投影为直线。 (2)曲线上的点的投影必定在曲线的同面投影上,即点与曲线的从属关系不变。 (3)一般情况下平面曲线投影的次数不变。即二次曲线的投影仍为二次曲线。 (4)曲线切线的投影仍为曲线投影的切线(图 5-3)。 5.1.1 圆的投影 圆是最常见的平面曲线,圆的正投影可能有三种情况:当圆所在平面平行于投影面时, 其投影仍为圆。当圆所在平面垂直于投影面时,则其投影为直线。当圆所在平面倾斜于投影 面时,则其投影为椭圆。 下面根据不同情况分别讨论在正投影图中,圆的投影及其作图。 1.圆所在的平面为投影面平行面 当圆所在的平面为投影面平行面时,圆在所平行的投 影面上的投影反映该圆的实形。在另一投影面上的投影为直线,线段的长度等于圆的直径(见 图 5-4)。 2.圆所在的平面为投影面垂直面 当圆所在的平面为投影面垂直面时,圆在所垂直的投 影面上的投影为直线,线段的长度等于直径。在另一投影面上的投影则为椭圆。 a b c d e l k A B C D E T t L a o b c d X a b o c d 图 5-3 平面曲线的投影性质 图 5-4 平行投影面的圆的投影 a c b d a b A B C D O X X a c d b a b c d d c o o o o Dcos D 1 2 1 2 1 2 X a)直观图 b)投影图 图 5-5 投影面垂直面上的圆
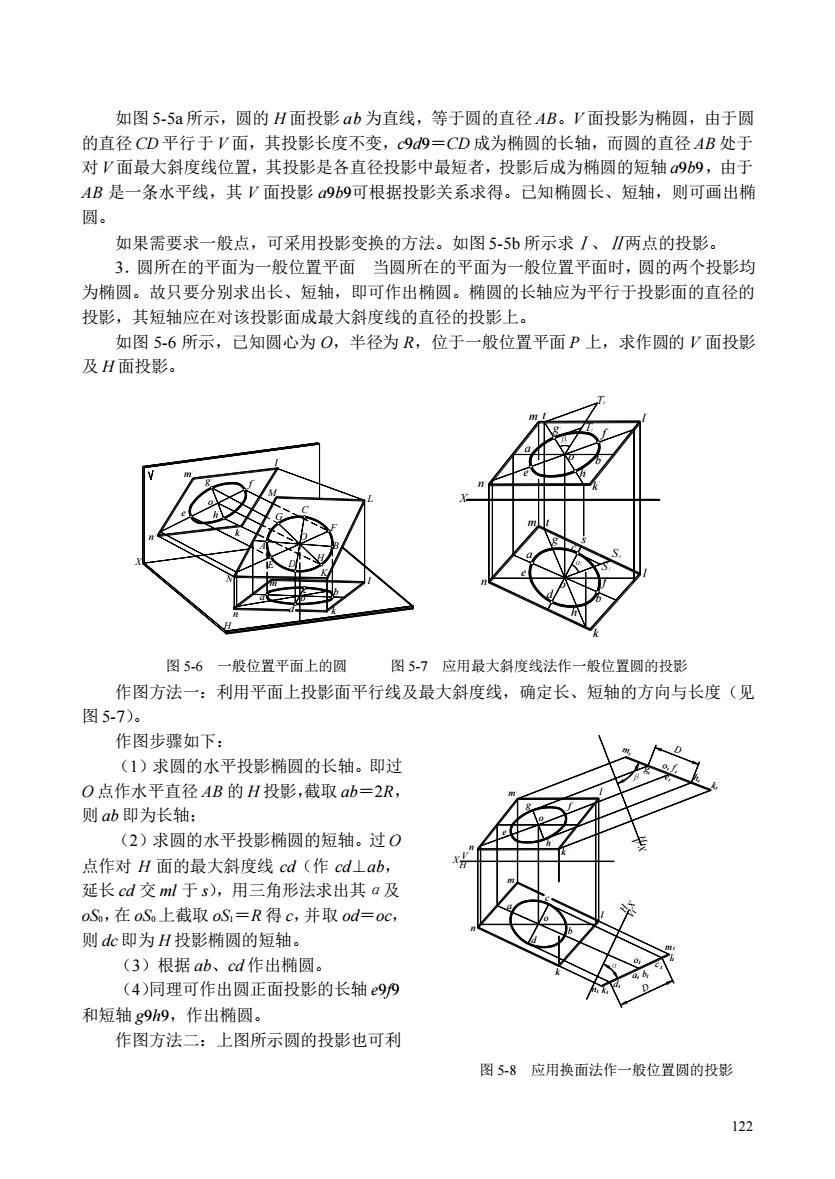
如图55a所示,圆的H面投影ab为直线,等于圆的直径AB。V面投影为椭圆,由于圆 的直径CD平行于V面,其投影长度不变,99=CD成为椭圆的长轴,而圆的直径AB处于 对V面最大斜度线位置,其投影是各直径投影中最短者,投影后成为椭圆的短轴a969,由于 AB是一条水平线,其V面投影9b9可根据投影关系求得。已知椭圆长、短轴,则可画出椭 圆。 如果需要求一般点,可采用投影变换的方法。如图5-5b所示求/、两点的投影。 3.圆所在的平面为一般位置平面当圆所在的平面为一般位置平面时,圆的两个投影均 为椭圆。故只要分别求出长、短轴,即可作出椭圆。椭圆的长轴应为平行于投影面的直径的 投影,其短轴应在对该投影面成最大斜度线的直径的投影上。 如图5-6所示,已知圆心为O,半径为R,位于一般位置平面P上,求作圆的V面投影 及H面投影。 图5-6一般位置平面上的圆 图57应用最大斜度线法作一般位置圆的投影 作图方法一:利用平面上投影面平行线及最大斜度线,确定长、短轴的方向与长度(见 图5-7)。 作图步骤如下: (1)求圆的水平投影椭圆的长轴。即过 O点作水平直径AB的H投影,截取ab=2R, 则ab即为长轴: (2)求圆的水平投影椭圆的短轴。过0 点作对H面的最大斜度线cd(作cd⊥ab, 延长cd交ml于s),用三角形法求出其a及 oS,在oS上截取oS=R得c,并取od=oC, 则dc即为H投影椭圆的短轴。 (3)根据ab、cd作出椭圆 (4)同理可作出圆正面投影的长轴e9/9 和短轴g99,作出椭圆。 作图方法二:上图所示圆的投影也可利 图58应用换面法作一般位置圆的投影 122
122 如图 5-5a 所示,圆的 H 面投影 ab 为直线,等于圆的直径 AB。V 面投影为椭圆,由于圆 的直径 CD 平行于 V 面,其投影长度不变,cd=CD 成为椭圆的长轴,而圆的直径 AB 处于 对 V 面最大斜度线位置,其投影是各直径投影中最短者,投影后成为椭圆的短轴 ab,由于 AB 是一条水平线,其 V 面投影 ab可根据投影关系求得。已知椭圆长、短轴,则可画出椭 圆。 如果需要求一般点,可采用投影变换的方法。如图 5-5b 所示求Ⅰ、Ⅱ两点的投影。 3.圆所在的平面为一般位置平面 当圆所在的平面为一般位置平面时,圆的两个投影均 为椭圆。故只要分别求出长、短轴,即可作出椭圆。椭圆的长轴应为平行于投影面的直径的 投影,其短轴应在对该投影面成最大斜度线的直径的投影上。 如图 5-6 所示,已知圆心为 O,半径为 R,位于一般位置平面 P 上,求作圆的 V 面投影 及 H 面投影。 作图方法一:利用平面上投影面平行线及最大斜度线,确定长、短轴的方向与长度(见 图 5-7)。 作图步骤如下: (1)求圆的水平投影椭圆的长轴。即过 O 点作水平直径 AB 的 H 投影,截取 ab=2R, 则 ab 即为长轴; (2)求圆的水平投影椭圆的短轴。过 O 点作对 H 面的最大斜度线 cd(作 cd⊥ab, 延长 cd 交 ml 于 s),用三角形法求出其α及 oS0,在 oS0 上截取 oS1=R 得 c,并取 od=oc, 则 dc 即为 H 投影椭圆的短轴。 (3)根据 ab、cd 作出椭圆。 (4)同理可作出圆正面投影的长轴 ef 和短轴 gh,作出椭圆。 作图方法二:上图所示圆的投影也可利 A B C E D F G H L K M N X O a c b d l k m n o m n l k g e h f o H a b c d e f g h l k m n o s X T T S S t m t g f l k b h o a e n 图 5-6 一般位置平面上的圆 图 5-7 应用最大斜度线法作一般位置圆的投影 D n 1 1 1 1 1 1 1 1 1 l m c o a b d n k b o c a d k n m l l k g h f e o m D X X H V X 1V H o1 V 1 H m1 k1 h1 1 g 1 f e1 图 5-8 应用换面法作一般位置圆的投影
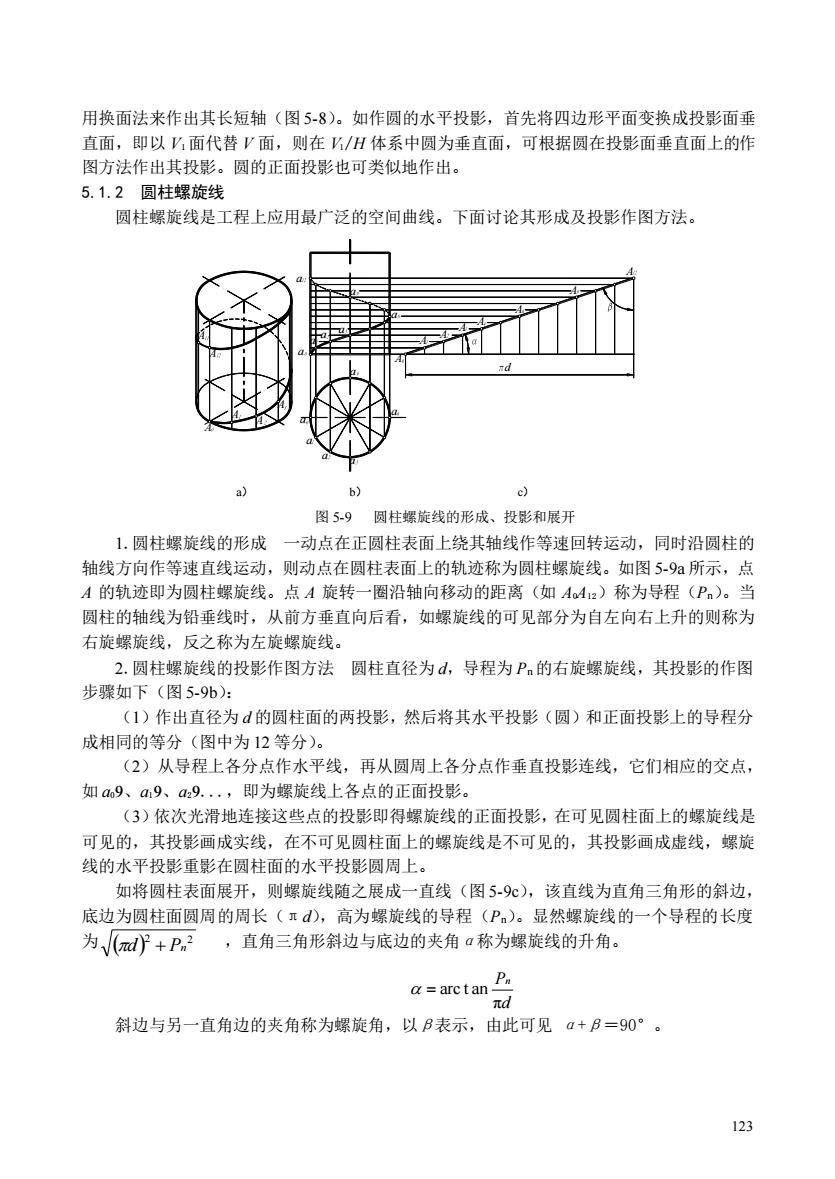
用换面法来作出其长短轴(图5-8)。如作圆的水平投影,首先将四边形平面变换成投影面垂 直面,即以V面代替V面,则在V/H体系中圆为垂直面,可根据圆在投量影面垂直面上的作 图方法作出其投影。圆的正面投影也可类似地作出 5.1.2圆柱螺旋线 圆柱螺旋线是工程上应用最广泛的空间曲线。下面讨论其形成及投影作图方法。 b) c 图5-9圆柱螺旋线的形成、投影和展开 1.圆柱螺旋线的形成一动点在正圆柱表面上绕其轴线作等速回转运动,同时沿圆柱的 轴线方向作等速直线运动,则动点在圆柱表面上的轨迹称为圆柱螺旋线。如图5-9妇所示,点 A的轨迹即为圆柱螺旋线。点A旋转一圈沿轴向移动的距离(如A4z)称为导程(P)。当 圆柱的轴线为铅垂线时,从前方垂直向后看,如螺旋线的可见部分为自左向右上升的则称为 右旋螺旋线,反之称为左旋螺旋线。 2.圆柱螺旋线的投影作图方法圆柱直径为d,导程为P的右旋螺旋线,其投影的作图 步骤如下(图5-9b): (1)作出直径为d的圆柱面的两投影,然后将其水平投影(圆)和正面投影上的导程分 成相同的等分(图中为12等分)。 (2)从导程上各分点作水平线,再从圆周上各分点作垂直投影连线,它们相应的交点 如a9、a9、a9.,即为螺旋线上各点的正面投影。 (3)依次光滑地连接这些点的投影即得螺旋线的正面投影,在可见圆柱面上的螺旋线是 可见的,其投影画成实线,在不可见圆柱面上的螺旋线是不可见的,其投影画成虚线,螺旋 线的水平投影重影在圆柱面的水平投影圆周上。 如将圆柱表面展开,则螺旋线随之展成一直线(图5-9),该直线为直角三角形的斜边, 底边为圆柱面圆周的周长(πd),高为螺旋线的导程(P)。显然螺旋线的一个导程的长度 为Vd}+P ,直角三角形斜边与底边的夹角α称为螺旋线的升角。 a-arctan P. 斜边与另一直角边的夹角称为螺旋角,以B表示,由此可见a+B=90°。 22
123 ( ) 2 2 d + Pn 用换面法来作出其长短轴(图 5-8)。如作圆的水平投影,首先将四边形平面变换成投影面垂 直面,即以 V1 面代替 V 面,则在 V1/H 体系中圆为垂直面,可根据圆在投影面垂直面上的作 图方法作出其投影。圆的正面投影也可类似地作出。 5.1.2 圆柱螺旋线 圆柱螺旋线是工程上应用最广泛的空间曲线。下面讨论其形成及投影作图方法。 1.圆柱螺旋线的形成 一动点在正圆柱表面上绕其轴线作等速回转运动,同时沿圆柱的 轴线方向作等速直线运动,则动点在圆柱表面上的轨迹称为圆柱螺旋线。如图 5-9a 所示,点 A 的轨迹即为圆柱螺旋线。点 A 旋转一圈沿轴向移动的距离(如 A0A12)称为导程(Pn)。当 圆柱的轴线为铅垂线时,从前方垂直向后看,如螺旋线的可见部分为自左向右上升的则称为 右旋螺旋线,反之称为左旋螺旋线。 2.圆柱螺旋线的投影作图方法 圆柱直径为 d,导程为 Pn 的右旋螺旋线,其投影的作图 步骤如下(图 5-9b): (1)作出直径为 d 的圆柱面的两投影,然后将其水平投影(圆)和正面投影上的导程分 成相同的等分(图中为 12 等分)。 (2)从导程上各分点作水平线,再从圆周上各分点作垂直投影连线,它们相应的交点, 如 a0、a1、a2.,即为螺旋线上各点的正面投影。 (3)依次光滑地连接这些点的投影即得螺旋线的正面投影,在可见圆柱面上的螺旋线是 可见的,其投影画成实线,在不可见圆柱面上的螺旋线是不可见的,其投影画成虚线,螺旋 线的水平投影重影在圆柱面的水平投影圆周上。 如将圆柱表面展开,则螺旋线随之展成一直线(图 5-9c),该直线为直角三角形的斜边, 底边为圆柱面圆周的周长(πd),高为螺旋线的导程(Pn)。显然螺旋线的一个导程的长度 为 ,直角三角形斜边与底边的夹角α称为螺旋线的升角。 斜边与另一直角边的夹角称为螺旋角,以β表示,由此可见 α+β=90°。 A A A A A A A A A A A A A A a a a a a a a a a a a a a d a) b) c) 图 5-9 圆柱螺旋线的形成、投影和展开 d Pn π = arc t an

5.2曲面的形成与表达方法 5.2.1概述 1.曲面的形成与分类 (1)曲面的形成曲面可以用不同的方式给定,在画法几何学中,主要以运动方法来 研究曲面的形成(并根据运动规律解决曲面上的定位问题和度量问题),曲面可以看作一条线 在空间按一定规律连续运动而成,或者说曲面是动线所有位置的集合。 形成曲面的动线称为母线,该线可以是直线,也可以是曲线,其形状可以是不变的,也 可以是不断变化的。 控制母线运动规律的线或面称为导线或导面。母线按规律运 动形成的曲面称为规则曲面。母线也可作不规则运动,形成的曲 面称为不规则曲面。 同一个曲面常可以用不同的方法形成。如圆柱面(图5-10) 可以是圆母线沿轴线方向平移而成,也可以是直母线绕轴线旋转 而成。还可以是以各点距轴线等远的曲线作母线,绕轴线旋转形 成圆柱面。在以上不同形式的母线中,一般应采用最简单的母线 来描述曲面的形成。 (2)曲面的分类根据不同的分类标准,曲面可有许多不同 图5-10曲面的形成 的分类方法。如:按母线的形状分类,曲面可分为直线面和曲线面:按母线的运动情况分类 曲面可分为移动面和回转面:按母线在运动中是否变化分类,曲面可分为定母线面和变母线 面:按母线运动是否有规律来分类,曲面可分为规则曲面和不规则曲面:按曲面是否能无皱 褚地难平在一个平面上来分类,则可分为可展曲面和不可展曲面。 按以上各种方法分类,对于同类曲面可能会有跨种类的现象,例如同属直线面的两个曲 面,就有可能分属于可展曲面和不可展曲面。 下面是一个按母线的性质来划分一些规则曲面的简表: 可展幽面 直线面 直线回转面 双曲回转 双曲物面 不可展曲面 曲线面 椭圆面、韩阅抛物面 本章重点介绍规则曲面中定母线运动形成的 曲面,并以直线面为主,对于曲线面,则只介死 曲线回转面。 2.曲面的投影在投影图上表示一个曲面, 只要作出能够确定曲面的几何要素的必要投影, 就可确定一个曲面,因为母线、导线或导面给定 以后,形成的曲面将唯一确定在实际作图中,为 了更加形象地表示曲面,除了给出几何要素外, 还要画出曲面外形轮廓线的投影。曲面的外形轮 图5-11曲面的投影 124
124 5.2 曲面的形成与表达方法 5.2.1 概述 1.曲面的形成与分类 (1)曲面的形成 曲面可以用不同的方式给定,在画法几何学中,主要以运动方法来 研究曲面的形成(并根据运动规律解决曲面上的定位问题和度量问题),曲面可以看作一条线 在空间按一定规律连续运动而成,或者说曲面是动线所有位置的集合。 形成曲面的动线称为母线,该线可以是直线,也可以是曲线,其形状可以是不变的,也 可以是不断变化的。 控制母线运动规律的线或面称为导线或导面。母线按规律运 动形成的曲面称为规则曲面。母线也可作不规则运动,形成的曲 面称为不规则曲面。 同一个曲面常可以用不同的方法形成。如圆柱面(图 5-10) 可以是圆母线沿轴线方向平移而成,也可以是直母线绕轴线旋转 而成。还可以是以各点距轴线等远的曲线作母线,绕轴线旋转形 成圆柱面。在以上不同形式的母线中,一般应采用最简单的母线 来描述曲面的形成。 (2)曲面的分类 根据不同的分类标准,曲面可有许多不同 的分类方法。如:按母线的形状分类,曲面可分为直线面和曲线面;按母线的运动情况分类, 曲面可分为移动面和回转面;按母线在运动中是否变化分类,曲面可分为定母线面和变母线 面;按母线运动是否有规律来分类,曲面可分为规则曲面和不规则曲面;按曲面是否能无皱 褶地摊平在一个平面上来分类,则可分为可展曲面和不可展曲面。 按以上各种方法分类,对于同类曲面可能会有跨种类的现象,例如同属直线面的两个曲 面,就有可能分属于可展曲面和不可展曲面。 下面是一个按母线的性质来划分一些规则曲面的简表: 曲面 直线面 柱面、锥面、切线面 可展曲面 直线回转面 圆柱面、圆锥面 单叶双曲回转面 不可展曲面 柱状面、锥状面、双曲抛物面 曲线面 曲线回转面 椭圆面、椭圆抛物面 本章重点介绍规则曲面中定母线运动形成的 曲面,并以直线面为主,对于曲线面,则只介绍 曲线回转面。 2.曲面的投影 在投影图上表示一个曲面, 只要作出能够确定曲面的几何要素的必要投影, 就可确定一个曲面,因为母线、导线或导面给定 以后,形成的曲面将唯一确定在实际作图中,为 了更加形象地表示曲面,除了给出几何要素外, 还要画出曲面外形轮廓线的投影。曲面的外形轮 图 5-10 曲面的形成 T t H 图 5-11 曲面的投影