月因推令月 图224判断两直线是否垂直 图225判断两直线是否垂直求 图2-26AB、CD两直线的公垂线 【例1】求AB、CD两直线的公垂线。(图2-26) 分析:直线AB是铅垂线,CD是一般位置直线,所以它们的公垂线是一条水平线。 作图: (1)由直线AB积聚的水平投影a(b)向cd作垂线交于k,再由此求出k。 (2)由k'向ab作垂线交于e',ek和ek即为公垂线EK的两投影。 【例2】己知菱形ABCD的一条对角线AC为正平线,菱形的一边位于直线AM上,求 该菱形的投影(图2-27a)。 图2-27求菱形ABCD的投影
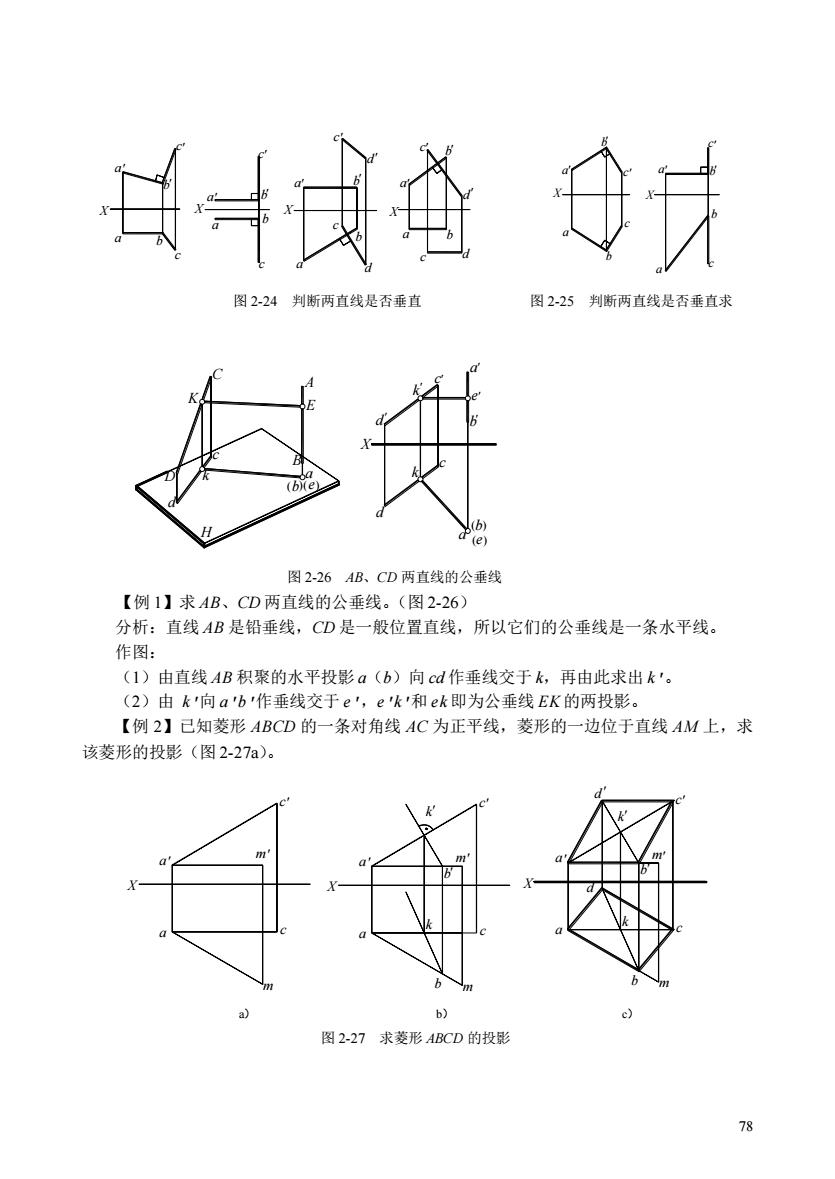
78 【例 1】求 AB、CD 两直线的公垂线。(图 2-26) 分析:直线 AB 是铅垂线,CD 是一般位置直线,所以它们的公垂线是一条水平线。 作图: (1)由直线 AB 积聚的水平投影 a(b)向 cd 作垂线交于 k,再由此求出 k'。 (2)由 k'向 a'b'作垂线交于 e',e'k'和 ek 即为公垂线 EK 的两投影。 【例 2】已知菱形 ABCD 的一条对角线 AC 为正平线,菱形的一边位于直线 AM 上,求 该菱形的投影(图 2-27a)。 X X X X a b c a b c a b c a b c a b a b c d c d a b a b c d c d ' ' ' ' ' ' ' ' ' ' ' ' ' ' X X a b c a b c a b c a b c ' ' ' ' ' ' 图 2-24 判断两直线是否垂直 图 2-25 判断两直线是否垂直求 A B C a b c H a b c c b a X d D k K E ( )(e) d d k k (e ) e ( ) ' ' ' ' ' ' 图 2-26 AB、CD 两直线的公垂线 X a a m m c c k k b b d X d a b m k c a b m c X a m c a c k m ' ' ' ' ' ' ' ' ' ' ' ' ' ' a) b) c) 图 2-27 求菱形 ABCD 的投影

分析:由菱形的定义可知,其对边互相平行,对角线互相垂直且平分。另对角线4C为 正平线,可利用平分、直角投影定理、平行投影作图。 作图: (1)在对角线AC上取中点K,即使a'k'=k'c',ak=kc。K点也必定为另一对角线的 中点。 (2)AC是正平线,故另一对角线的正面投影必定垂直AC的正面投影a'c'。因此过k 作kbLa'c',并与a'm交于b',由kb求出b(图2-27b)。 (3)在对角线KB的延长线上取一点D,使KD=KB,即k'd=kb',kd=仙,则b'd' 和bd即为另一对角线的投影,连接各点即为菱形ABCD的投影(图2-27c)。 观察与思考:观察周围,试着抽象出两直线平行、相交、交叉关系的几何问题,并试者 图示 2.3平面的投影 平面是物体表面的重要组成部分,也是主要的空间几何元素之一。其表示方法有如下两 种。 (1)几何元素表示法由初等几何得知,下列几何元素组都可以决定平面在空间的位置: 1)不在同一直线上的三个点。 2)直线和直线外的一点。 3)相交两直线。 4)平行两直线。 5)任意平面图形,如三角形、平行四边形、圆形等。 如图2-28是用各组几何元素所表示的同一平面的投影图。显然各组几何元素是可以互相 转换的,如连接AB即可由图a转换成图b:再连接AC,又可转换成图c,将A、B、C、三点彼 此连结又可转换成图等。从图中可以看出,不在同一直线上的三个点是决定平面位置的基本 几何元素组 +串传自念 图2-28平面的表示法及其投影图 (2)迹线表示法迹线表示法是用平面上的特殊直线来表示平面的方法。如图2-29所 示:该特殊直线是平面与投影面的交线,称为迹线。平面P与H、八、W面的交线分别称为水 平迹线、正面迹线和侧面迹线,以P4、P、P表示。两两相交于、X、Z轴上的一点称为迹 线集合点,分别以Px、P、P表示。 由于迹线在投影面上,故迹线在该投影面上的投影必与其本身重合,规定用迹线符号标 70
79 分析:由菱形的定义可知,其对边互相平行,对角线互相垂直且平分。另对角线 AC 为 正平线,可利用平分、直角投影定理、平行投影作图。 作图: (1)在对角线 AC 上取中点 K,即使 a'k'=k'c',ak=kc。K 点也必定为另一对角线的 中点。 (2)AC 是正平线,故另一对角线的正面投影必定垂直 AC 的正面投影 a'c'。因此过 k' 作 k'b'⊥a'c',并与 a'm'交于 b',由 k'b'求出 kb(图 2-27b)。 (3)在对角线 KB 的延长线上取一点 D,使 KD=KB,即 k'd'=k'b',kd=kb,则 b'd' 和 bd 即为另一对角线的投影,连接各点即为菱形 ABCD 的投影(图 2-27c)。 观察与思考:观察周围,试着抽象出两直线平行、相交、交叉关系的几何问题,并试着 图示。 2.3 平面的投影 平面是物体表面的重要组成部分,也是主要的空间几何元素之一。其表示方法有如下两 种。 (1)几何元素表示法 由初等几何得知,下列几何元素组都可以决定平面在空间的位置: 1)不在同一直线上的三个点。 2)直线和直线外的一点。 3)相交两直线。 4)平行两直线。 5)任意平面图形,如三角形、平行四边形、圆形等。 如图2-28是用各组几何元素所表示的同一平面的投影图。显然各组几何元素是可以互相 转换的,如连接AB即可由图a转换成图b;再连接AC,又可转换成图c,将A、B、C、三点彼 此连结又可转换成图e等。从图中可以看出,不在同一直线上的三个点是决定平面位置的基本 几何元素组。 (2)迹线表示法 迹线表示法是用平面上的特殊直线来表示平面的方法。如图2-29所 示:该特殊直线是平面与投影面的交线,称为迹线。平面P与H、V、W面的交线分别称为水 平迹线、正面迹线和侧面迹线,以PH、PV、PW表示。两两相交于X、Y、Z轴上的一点称为迹 线集合点, 分别以PX、PY、PZ表示。 由于迹线在投影面上,故迹线在该投影面上的投影必与其本身重合,规定用迹线符号标 a c b a c b d d a c a c b b a c a c b b a c a c b b a c a c b b ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' X O X O X O X O X O a) b) c) d) e) 图 2-28 平面的表示法及其投影图
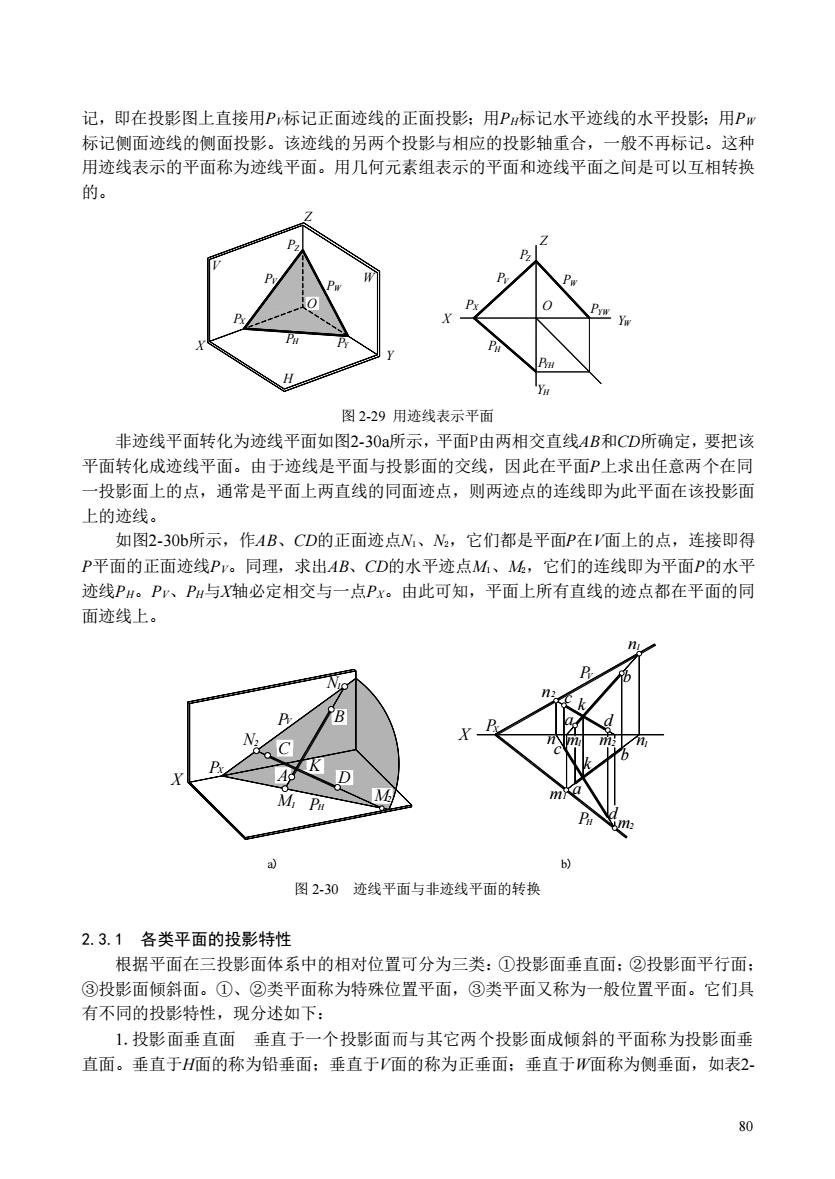
记,即在投影图上直接用P标记正面迹线的正面投影:用P标记水平迹线的水平投影:用Pw 标记侧面迹线的侧面投影。该迹线的另两个投影与相应的投影轴重合,一般不再标记。这种 用迹线表示的平面称为迹线平面。用几何元素组表示的平面和迹线平面之间是可以互相转换 的。 图2-29用迹线表示平面 非迹线平面转化为迹线平面如图2-30a所示,平面P由两相交直线4B和CD所确定,要把该 平面转化成迹线平面。由于迹线是平面与投影面的交线,因此在平面P上求出任意两个在同 一投影面上的点,通常是平面上两直线的同面迹点,则两迹点的连线即为此平面在该投影面 上的迹线。 如图2-30b所示,作AB、CD的正面迹点N、,它们都是平面P在面上的点,连接即得 P平面的正面迹线P。同理,求出AB、CD的水平迹点M、k,它们的连线即为平面P的水平 迹线PH。P、PH与X轴必定相交与一点Px。由此可知,平面上所有直线的迹点都在平面的同 面迹线上。 A 。C D 图2-30迹线平面与非迹线平面的转换 2.3.1各类平面的投影特性 根据平面在三投影面体系中的相对位置可分为三类:①投影面垂直面:②投影面平行面 ③投影面倾斜面。①、②类平面称为特殊位置平面,③类平面又称为一般位置平面。它们具 有不同的投影特性,现分述如下: 1.投影面垂直面垂直于一个投最影面而与其它两个投景影面成頓斜的平面称为投景影面垂 直面。垂直于H面的称为铅垂面:垂直于面的称为正垂面:垂直于W面称为侧垂面,如表2 80
80 记,即在投影图上直接用PV标记正面迹线的正面投影;用PH标记水平迹线的水平投影;用PW 标记侧面迹线的侧面投影。该迹线的另两个投影与相应的投影轴重合,一般不再标记。这种 用迹线表示的平面称为迹线平面。用几何元素组表示的平面和迹线平面之间是可以互相转换 的。 V W H W YW W H YH H X Z V H Y W Z X V O X Z Y Y Y Z X P P P P P P P P P P P P O P 图 2-29 用迹线表示平面 非迹线平面转化为迹线平面如图2-30a所示,平面P由两相交直线AB和CD所确定,要把该 平面转化成迹线平面。由于迹线是平面与投影面的交线,因此在平面P上求出任意两个在同 一投影面上的点,通常是平面上两直线的同面迹点,则两迹点的连线即为此平面在该投影面 上的迹线。 如图2-30b所示,作AB、CD的正面迹点N1、N2,它们都是平面P在V面上的点,连接即得 P平面的正面迹线PV。同理,求出AB、CD的水平迹点M1、M2,它们的连线即为平面P的水平 迹线PH。PV、PH与X轴必定相交与一点PX。由此可知,平面上所有直线的迹点都在平面的同 面迹线上。 2 1 2 1 m 1 a n m m d c k b m n a d c k b n n X PH 1 PV 2 PX 1 2 V 1 H 2 X X P C M N P N B D M P K A a) b) 图 2-30 迹线平面与非迹线平面的转换 2.3.1 各类平面的投影特性 根据平面在三投影面体系中的相对位置可分为三类:①投影面垂直面;②投影面平行面; ③投影面倾斜面。①、②类平面称为特殊位置平面,③类平面又称为一般位置平面。它们具 有不同的投影特性,现分述如下: 1.投影面垂直面 垂直于一个投影面而与其它两个投影面成倾斜的平面称为投影面垂 直面。垂直于H面的称为铅垂面;垂直于V面的称为正垂面;垂直于W面称为侧垂面,如表2-
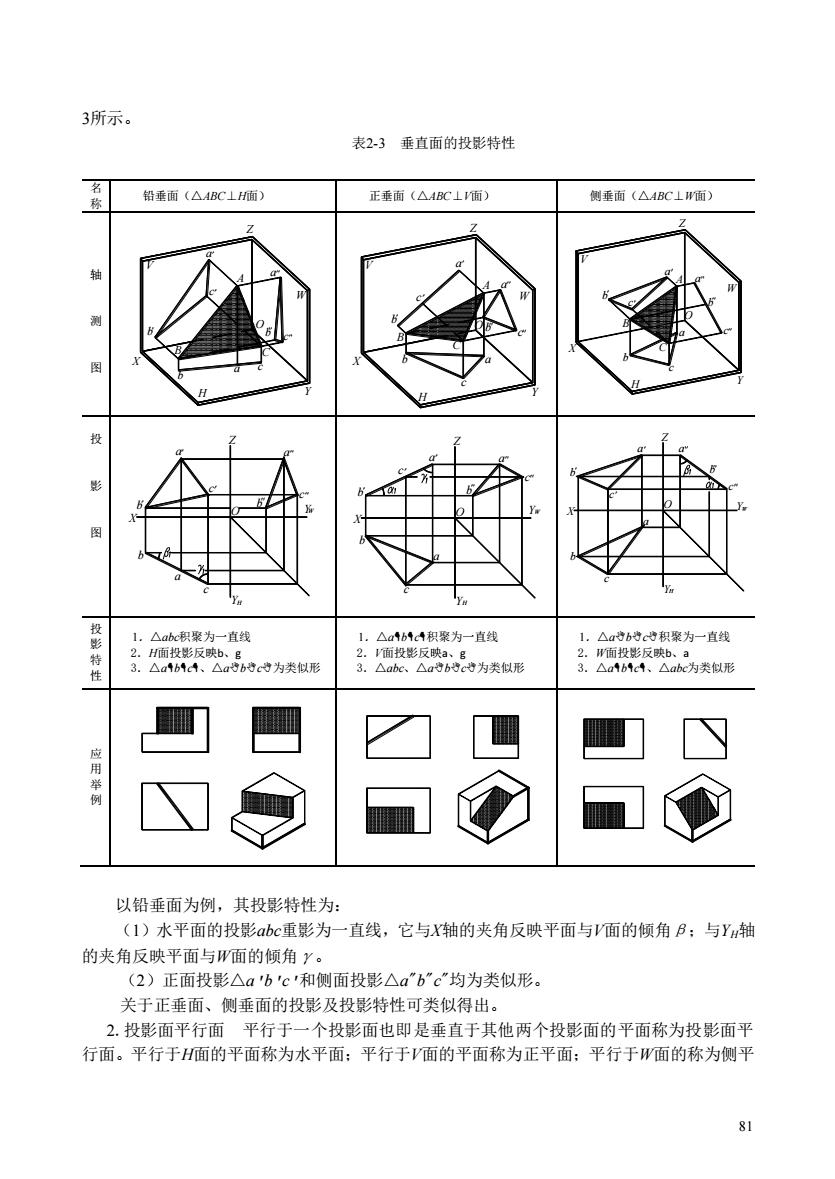
3所示。 表23垂直面的投影特性 铅垂面(△BCH) 正垂面(△BC⊥面) 侧垂面(△4BC⊥W面) 投影特 △abc积聚为一直线 △4b14积聚为一直线 ,△ab的c积聚为一直线 子影反为天形 以铅垂面为例,其投影特性为: (1)水平面的投影abc重影为一直线,它与X轴的夹角反映平面与V面的倾角B与Y轴 的夹角反映平面与W面的倾角y。 (2)正面投影△ab'c'和侧面投影△abc均为类似形。 关于正垂面、侧垂面的投影及投影特性可类似得出。 2.投影面平行面平行于一个投影面也即是垂直于其他两个投影面的平面称为投影面平 行面。平行于面的平面称为水平面:平行于面的平面称为正平面:平行于W面的称为侧平 81
81 3所示。 表2-3 垂直面的投影特性 名 称 铅垂面(△ABC⊥H面) 正垂面(△ABC⊥V面) 侧垂面(△ABC⊥W面) 轴 测 图 X Y Z b a c B A C b a c b a c O V H W X Y Z b c a B C A b c a a b c O V W H X Y Z b a c B C A a c b a b c O W H V 投 影 图 b YH a c X b a c O Z a b c YW b YH c a X b a c b O Z a YW c c b YH a X b a a c O Z b Y c W 投 影 特 性 1.△abc积聚为一直线 2.H面投影反映b、g 3.△abc、△abc为类似形 1.△abc积聚为一直线 2.V面投影反映a、g 3.△abc、△abc为类似形 1.△abc积聚为一直线 2.W面投影反映b、a 3.△abc、△abc为类似形 应 用 举 例 以铅垂面为例,其投影特性为: (1)水平面的投影abc重影为一直线,它与X轴的夹角反映平面与V面的倾角β;与YH轴 的夹角反映平面与W面的倾角γ。 (2)正面投影△a'b'c'和侧面投影△a"b"c"均为类似形。 关于正垂面、侧垂面的投影及投影特性可类似得出。 2.投影面平行面 平行于一个投影面也即是垂直于其他两个投影面的平面称为投影面平 行面。平行于H面的平面称为水平面;平行于V面的平面称为正平面;平行于W面的称为侧平
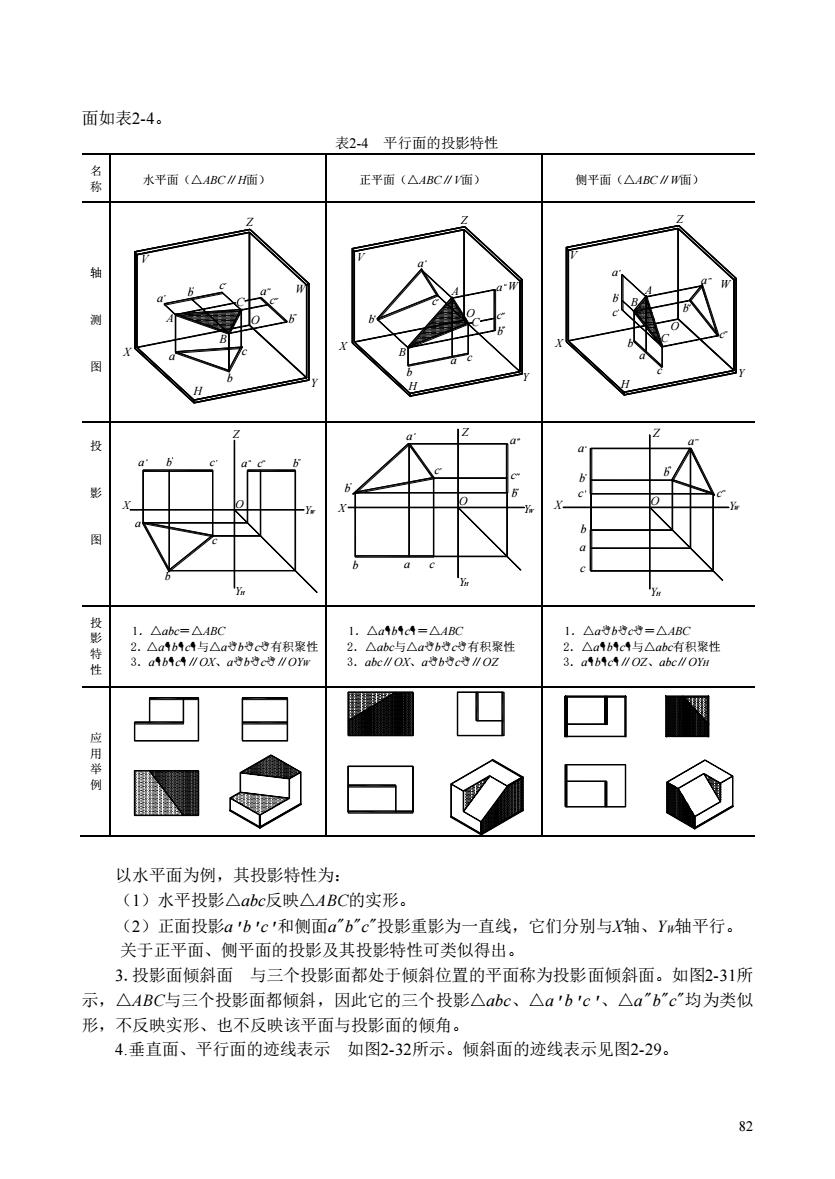
面如表24。 表24平行面的投影特性 水平面(△BCMH面) 正平面(△BC∥1面) 侧平面(△BC∥#面) 投影特 1.△ab=△ABC 1.△aAb4cA=△4B 1.△a待b0c等=△AB0 以水平面为例,其投影特性为: (1)水平投影△abc反映△ABC的实形。 (2)正面投影ab'c'和侧面abc"投影重影为一直线,它们分别与X轴、Yw轴平行。 关于正平面、侧平面的投影及其投影特性可类似得出。 3.投影面倾斜面与三个投影面都处于倾斜位置的平面称为投影面倾斜面。如图2-31所 示,△ABC与三个投影面都倾斜,因此它的三个投影△abc、△a'b'c'、△a“b"c"均为类似 形,不反映实形、也不反映该平面与投影面的倾角。 4.垂直面、平行面的迹线表示如图2-32所示。倾斜面的迹线表示见图2-29。 82
82 面如表2-4。 表2-4 平行面的投影特性 名 称 水平面(△ABC∥H面) 正平面(△ABC∥V面) 侧平面(△ABC∥W面) 轴 测 图 X Z Y a b c A B C a b c a c O b V W H X Z Y b a c b c a a b c A C B O V W H c a b c b a a b c A B C X Z Y O V W H 投 影 图 H a a Y b c X a b O c Z c YW b H b Y a c X b O c a Z a b c YW YH c a b X b c a O Z W b c Y a 投 影 特 性 1.△abc=△ABC 2.△abc与△abc有积聚性 3.abc∥OX、abc∥OYW 1.△abc=△ABC 2.△abc与△abc有积聚性 3.abc∥OX、abc∥OZ 1.△abc=△ABC 2.△abc与△abc有积聚性 3.abc∥OZ、abc∥OYH 应 用 举 例 以水平面为例,其投影特性为: (1)水平投影△abc反映△ABC的实形。 (2)正面投影a'b'c'和侧面a"b"c"投影重影为一直线,它们分别与X轴、YW轴平行。 关于正平面、侧平面的投影及其投影特性可类似得出。 3.投影面倾斜面 与三个投影面都处于倾斜位置的平面称为投影面倾斜面。如图2-31所 示,△ABC与三个投影面都倾斜,因此它的三个投影△abc、△a'b'c'、△a"b"c"均为类似 形,不反映实形、也不反映该平面与投影面的倾角。 4.垂直面、平行面的迹线表示 如图2-32所示。倾斜面的迹线表示见图2-29