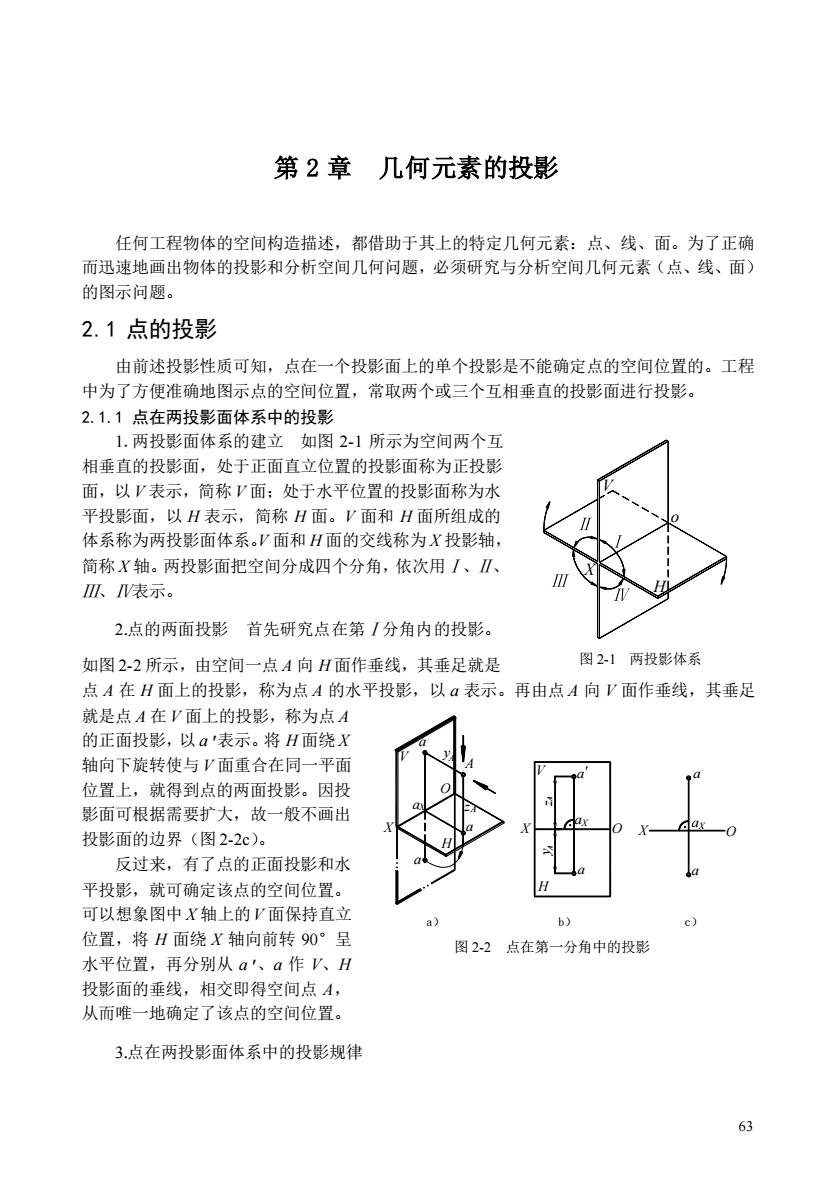
第2章几何元素的投影 任何工程物体的空间构造描述,都借助于其上的特定几何元素:点、线、面。为了正确 而迅速地画出物体的投影和分析空间几何问题,必须研究与分析空间几何元素(点、线、面) 的图示问题。 2.1点的投影 由前述投影性质可知,点在一个投影面上的单个投影是不能确定点的空间位置的。工程 中为了方便准确地图示点的空间位置,常取两个或三个互相垂直的投影面进行投影。 2.1.1点在两投影面体系中的投影 1.两投量影而体系的建立如图2.1所示为空间两个互 相垂直的投影面,处于正面直立位置的投影面称为正投影 面,以V表示,简称V面:处于水平位置的投影面称为水 平投影面,以H表示,简称H面。V面和H面所组成的 体系称为两投影面体系。V面和H面的交线称为X投影轴, 简称X轴。两投影面把空间分成四个分角,依次用/、Ⅱ、 、表示。 2点的两面投影首先研究点在第分角内的投影。 如图2-2所示,由空间一点A向H面作垂线,其垂足就是 图21两投影体系 点A在H面上的投影,称为点A的水平投影,以a表示。再由点A向V面作垂线,其垂足 就是点A在V面上的投影,称为点A 的正面投影,以a表示。将H面绕X 轴向下旋转使与V面重合在同一平面 位置上,就得到点的两面投影。因投 影面可根据需要扩大,故一般不画出 投影面的边界(图2-2c)。 反过来,有了点的正面投影和水 平投影,就可确定该点的空间位置。 可以想象图中X轴上的V面保持直立 b) 位置,将H面绕X轴向前转90°呈 图2-2点在第一分角中的投影 水平位置,再分别从a'、a作V、H 投影面的垂线,相交即得空间点A, 从而唯一地确定了该点的空间位置。 3.点在两投影面体系中的投影规律 63
63 第 2 章 几何元素的投影 任何工程物体的空间构造描述,都借助于其上的特定几何元素:点、线、面。为了正确 而迅速地画出物体的投影和分析空间几何问题,必须研究与分析空间几何元素(点、线、面) 的图示问题。 2.1 点的投影 由前述投影性质可知,点在一个投影面上的单个投影是不能确定点的空间位置的。工程 中为了方便准确地图示点的空间位置,常取两个或三个互相垂直的投影面进行投影。 2.1.1 点在两投影面体系中的投影 1.两投影面体系的建立 如图 2-1 所示为空间两个互 相垂直的投影面,处于正面直立位置的投影面称为正投影 面,以 V 表示,简称 V 面;处于水平位置的投影面称为水 平投影面,以 H 表示,简称 H 面。V 面和 H 面所组成的 体系称为两投影面体系。V 面和 H 面的交线称为 X 投影轴, 简称 X 轴。两投影面把空间分成四个分角,依次用Ⅰ、Ⅱ、 Ⅲ、Ⅳ表示。 2.点的两面投影 首先研究点在第Ⅰ分角内的投影。 如图 2-2 所示,由空间一点 A 向 H 面作垂线,其垂足就是 点 A 在 H 面上的投影,称为点 A 的水平投影,以 a 表示。再由点 A 向 V 面作垂线,其垂足 就是点 A 在 V 面上的投影,称为点 A 的正面投影,以 a'表示。将 H 面绕 X 轴向下旋转使与 V 面重合在同一平面 位置上,就得到点的两面投影。因投 影面可根据需要扩大,故一般不画出 投影面的边界(图 2-2c)。 反过来,有了点的正面投影和水 平投影,就可确定该点的空间位置。 可以想象图中 X 轴上的V 面保持直立 位置,将 H 面绕 X 轴向前转 90°呈 水平位置,再分别从 a'、a 作 V、H 投影面的垂线,相交即得空间点 A, 从而唯一地确定了该点的空间位置。 3.点在两投影面体系中的投影规律 图4-1 H V o X 图 2-1 两投影体系 a X X a A X a a a y a z a z y a a a A X A A A X X ' O O O V H V H a) b) c) 图 2-2 点在第一分角中的投影

由图2-2可知,Aaaa'是个矩形,aa、aa,都垂直X轴,H面向下旋转后,a、a的连线 aa' 一定垂直于X轴,由此可得出点的投影规律: (1)点的水平投影和正面投影的连线垂直X轴。即a'垂直X轴。 (2)点的水平投影到X轴的距离等于空间点到V面的距离。即aa,=Aa'。 (3)点的正面投影到X轴的距离等于空间点到H面的距离。即a'a,=Aa。 4.其他分角中点的投影 如图23所示,空间点B、C、D分别处于Ⅱ、瓜、分角中,各点分别向相应的投影面 作投射线,就可以得到各点的正面投影和水平投影。当前半的H面向下旋转(也即后半H 面向上旋转)与V面(面)重合后得到各点的投影图。显然这些点的投影也必定符合上述 投影规律,但各点的投影在图上的位置有如下的特点: b 图23其他分角中点的投影 第∥分角中的点B,正面投影b'和水平投影b同在X轴的上方。 第份角中的点C,正面投影c在轴下方,水平投影c在X轴上方。 第W分角中的点D, 正面投影d'和水平投影d 同在X轴下方。 5.投影面和投影轴上 点的投影在特殊情况 下,点也可以位于投影面 上和投影轴上。点在哪个 面上,它与这个投影面的 距离就为零,并且与该投 影面上的投影重合,而另 一投影在投影轴上。如图 2-4所示,点M在H面上, 图2-2投影面和轴上点的投影 64
64 由图 2-2 可知,Aaaxa '是个矩形,a 'ax、 aax都垂直 X 轴,H 面向下旋转后,a、a '的连线 aa' 一定垂直于 X 轴,由此可得出点的投影规律: (1)点的水平投影和正面投影的连线垂直 X 轴。即 aa'垂直 X 轴。 (2)点的水平投影到 X 轴的距离等于空间点到 V 面的距离。即 aax=Aa'。 (3)点的正面投影到 X 轴的距离等于空间点到 H 面的距离。即 a'ax=Aa 。 4.其他分角中点的投影 如图 2-3 所示,空间点 B、C、D 分别处于Ⅱ、Ⅲ、Ⅳ分角中,各点分别向相应的投影面 作投射线,就可以得到各点的正面投影和水平投影。当前半的 H 面向下旋转(也即后半 H1 面向上旋转)与 V 面(V1 面)重合后得到各点的投影图。显然这些点的投影也必定符合上述 投影规律,但各点的投影在图上的位置有如下的特点: X X X X X X H1 H V1 V O O X c X d c d b b d c b d b c b B b c C c d D d a) b) 图 2-3 其他分角中点的投影 第Ⅱ分角中的点 B,正面投影 b '和水平投影 b 同在 X 轴的上方。 第Ⅲ分角中的点 C,正面投影 c'在 X 轴下方,水平投影 c 在 X 轴上方。 第Ⅳ分角中的点 D, 正面投影 d'和水平投影 d 同在 X 轴下方。 5.投影面和投影轴上 点的投影 在特殊情况 下,点也可以位于投影面 上和投影轴上。点在哪个 面上,它与这个投影面的 距离就为零,并且与该投 影面上的投影重合,而另 一投影在投影轴上。如图 2-4 所示,点 M 在 H 面上, X k n m n l k k l g m k l l m m n n g g K L M G N ( ) ( ) ( ) ( ) ( ) ' ' ' ' ' ' ' ' ' ' O O X V V H H1 1 a) b) 图 2-2 投影面和轴上点的投影

则m与M重合,m'在X轴上,同理,点K也如此。点N在V面上,则n'与N重合,n在X 轴上,同理点L亦如此。当点在投影轴上时,它的两个投影均与空间点重合在投影轴上。如 点G在轴上,则g、g与G均重合在X轴上。 2.1.2点在三投影面体系中的投影 1.三投影面体系的建立如图2-5a所示,如在两面体系上再加上一个与人、H均垂直的 投影面,它处于侧立位置,称为侧投影面,以W表示,简称W面,这样三个互相垂直的面 就组成一个三投影面体系。H、W面的交线称为Y投影轴,简称Y轴:人、W面的交线称为Z 投影轴,简称Z轴,三个投影轴的交点O称为原点。 图2-5点在三投影面体系中的投影 2.点的三面投影设有一空间点A,分别向从、V、W面进行投射得a、a'、a”,a“称 为点A的侧面投影。将H、W面分别按箭头方向旋转,使与V面重合,即得点的三面投影(图 2-5b)。其中Y轴既随H面旋转,也随W面旋转,分别用YH.Yw表示。通常在投影图上只画 出其投影轴不画投影面的边界(图2-5c)。 3.点的直角坐标与三面投影的关系如把三投影面体系看做空间直角坐标系,则H、V、 W面即为坐标面,X、Y、Z轴即为坐标轴,O点即为坐标原点。由图25可知,点A的三个 直角坐标x、即为点A到三个坐标面的距离,它们与点A的投影的关系如下: A重喜W=Aa=aay=a'az=Oax=x一横标 A距肉W=Aa'=aaw=aaz=Oa=y→纵标 A里直W=4a=a'ar=aar=Oa2=一高标 由此可见:a由x、以确定: a'由xA、H确定: a由A、确定 所以空间点A(x,4,4)在三面投影体系中有唯一的一组投影(a,a',a”)。反之, 已知点A的投影(a,a',a),即可确定点A的空间坐标值。 3.三投影面体系中点的投影规律三投影面体系中点的投影规律如下: 65
65 则 m 与 M 重合,m'在 X 轴上,同理,点 K 也如此。点 N 在 V 面上,则 n'与 N 重合,n 在 X 轴上,同理点 L 亦如此。当点在投影轴上时,它的两个投影均与空间点重合在投影轴上。如 点 G 在 X 轴上,则 g、g'与 G 均重合在 X 轴上。 2.1.2 点在三投影面体系中的投影 1.三投影面体系的建立 如图 2-5a 所示,如在两面体系上再加上一个与 V、H 均垂直的 投影面,它处于侧立位置,称为侧投影面,以 W 表示,简称 W 面,这样三个互相垂直的面 就组成一个三投影面体系。H、W 面的交线称为 Y 投影轴,简称 Y 轴;V、W 面的交线称为 Z 投影轴,简称 Z 轴,三个投影轴的交点 O 称为原点。 2. 点的三面投影 设有一空间点 A,分别向 H、V、W 面进行投射得 a、a'、a",a"称 为点 A 的侧面投影。将 H、W 面分别按箭头方向旋转,使与 V 面重合,即得点的三面投影(图 2-5b)。其中 Y 轴既随 H 面旋转,也随 W 面旋转,分别用 YH、YW表示。通常在投影图上只画 出其投影轴不画投影面的边界(图 2-5c)。 3.点的直角坐标与三面投影的关系 如把三投影面体系看做空间直角坐标系,则 H、V、 W 面即为坐标面,X、Y、Z 轴即为坐标轴,O 点即为坐标原点。由图 2-5 可知,点 A 的三个 直角坐标 xA、yA、zA 即为点 A 到三个坐标面的距离,它们与点 A 的投影的关系如下: A 距 离 W=Aa"=aaY=a'aZ=OaX=xA 横标 A 距 离 W=Aa'=aaX=a"aZ=OaY=yA 纵标 A 距 离 W=Aa=a'aX=a"aY=OaZ=zA 高标 由此可见:a 由 xA、yA 确定; a'由 xA、zA 确定; a"由 yA、zA 确定 所以空间点 A(xA,yA,zA)在三面投影体系中有唯一的一组投影(a,a',a")。反之, 已知点 A 的投影(a,a',a"),即可确定点 A 的空间坐标值。 3.三投影面体系中点的投影规律 三投影面体系中点的投影规律如下: X Z Y a a a a a z a y x Z X W YH a a a A A A a X a YH X W Z a a Z a O O a Y O Y A A A X Z Y A a a aZ Y O Y aX z y x aO a a '' ' '' ' H W YH YW V H W a) b) c) 图 2-5 点在三投影面体系中的投影

(1)点的正面投影和水平投影的连线垂直于X轴。这两个投影都反映空间点的x(横) 坐标,即: aa'⊥X轴,a'az=aayH=xA (2)点的正面投影和侧面投影的连线垂直于Z轴。这两个投影都反映空间点的Z(高) 坐标,即: a'a”⊥Z轴,a'ar=a”aw=2 (3)点的水平投影到X轴的距离等于侧面投影到Z轴的距离。这两个投影都反映空间 点的Y坐(纵)标,即: aar=a"g=v 根据点的三面投影规律,可由点的三个坐标值画出三面投影图:也可根据点的两个投影 作出第三投影。 【例1】己知点A的坐标(20,15,10),点B的坐标(30,10,0),点C的坐标(15, 0,0),作出点的三面投影(图2-6)。 分析:由于B=0,点B在H面上,又由于℃=0,℃=0,点C在X轴上。 作图:点A的投影:从O点向左在X轴20处作垂线aa',然后在aa'上从X轴向下向 上分别取y⅓=15和=10,求出a和a',由a'作Z轴的垂线,然后从Z轴向右方取15即 得a”。 其他从略。 图2-6根据点的坐标作投影图 图2-7己知点的两投影求第三投影 【例2】已知点D的两个投影d,、d,求出其第三投影d。(图2-7)。 分析:由于已知点的正面投影d'和侧面投影d广,则点的空间位置可以确定,由此可以 作出其水平投影。 作图:根据点的投影规律,水平投影d到X轴的距离等于侧面投影广到Z轴的距离。先 从原点O作YH、Yw分角线,然后从d”引Yw的垂线与分角线相交,再由交点作X轴的平行 线与由d'作出的X轴的垂直线相交即得水平投影d。 【例3】己知点A的三面投影,画出其轴测图。(图2-8)。 66
66 (1)点的正面投影和水平投影的连线垂直于 X 轴。这两个投影都反映空间点的 x(横) 坐标,即: aa'⊥X 轴,a'aZ=aaYH=xA (2)点的正面投影和侧面投影的连线垂直于 Z 轴。这两个投影都反映空间点的 Z(高) 坐标,即: a'a"⊥Z 轴,a'aX=a"aYW=zA (3)点的水平投影到 X 轴的距离等于侧面投影到 Z 轴的距离。这两个投影都反映空间 点的 Y 坐(纵)标,即: aaX=a"aZ=yA 根据点的三面投影规律,可由点的三个坐标值画出三面投影图;也可根据点的两个投影 作出第三投影。 【例 1】已知点 A 的坐标(20,15,10),点 B 的坐标(30,10,0),点 C 的坐标(15, 0,0),作出点的三面投影(图 2-6)。 分析:由于 zB=0,点 B 在 H 面上,又由于 yC=0,zC=0,点 C 在 X 轴上。 作图:点 A 的投影:从 O 点向左在 X 轴 20 处作垂线 aa',然后在 aa'上从 X 轴向下向 上分别取 yA=15 和 zA=10,求出 a 和 a',由 a'作 Z 轴的垂线,然后从 Z 轴向右方取 15 即 得 a"。 其他从略。 【例 2】已知点 D 的两个投影 d'、d",求出其第三投影 d。(图 2-7)。 分析:由于已知点的正面投影 d'和侧面投影 d",则点的空间位置可以确定,由此可以 作出其水平投影。 作图:根据点的投影规律,水平投影 d 到 X 轴的距离等于侧面投影 d"到 Z 轴的距离。先 从原点 O 作 YH、YW分角线,然后从 d"引 YW的垂线与分角线相交,再由交点作 X 轴的平行 线与由 d'作出的 X 轴的垂直线相交即得水平投影 d。 【例 3】已知点 A 的三面投影,画出其轴测图。(图 2-8)。 Z X Y Y a a a b c c b c b H W O ' ' ' '' '' '' Z X Y Y O W H d d d ' '' 图 2-6 根据点的坐标作投影图 图 2-7 已知点的两投影求第三投影
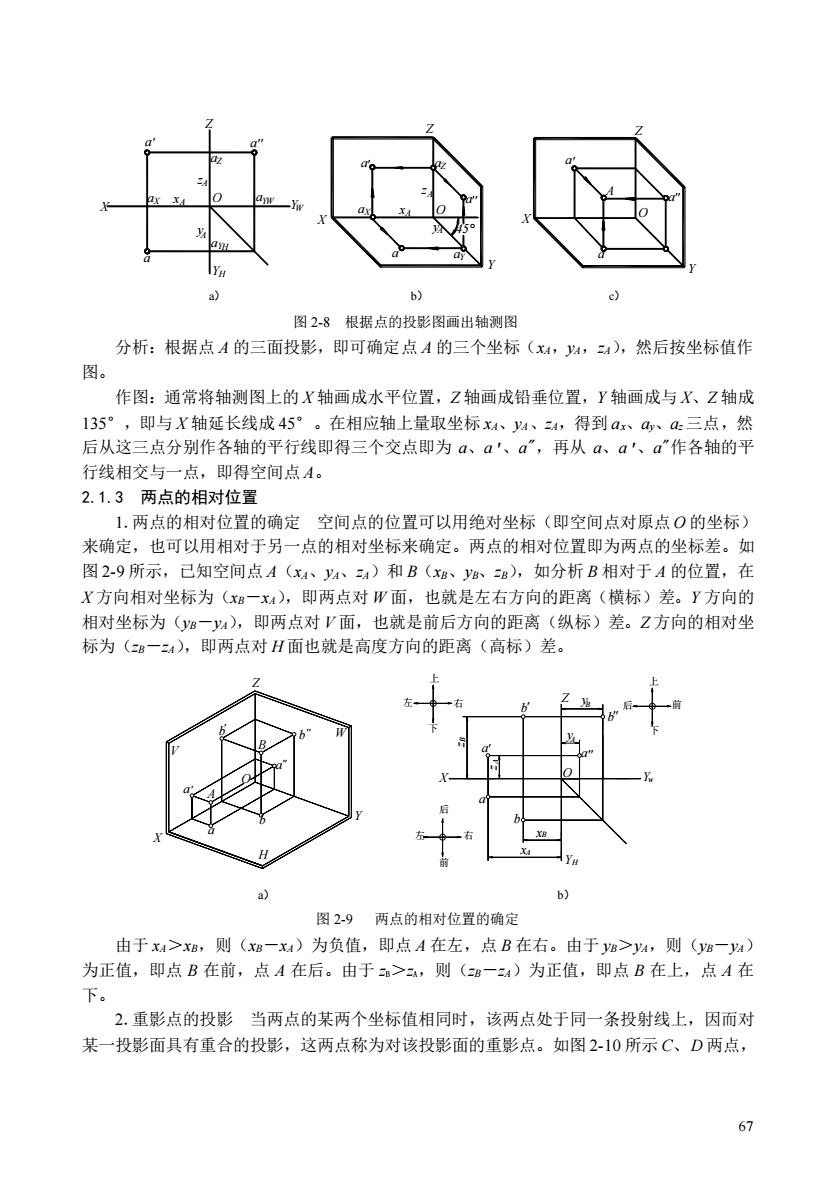
图28根据点的投影形图画出轴测图 分析:根据点A的三面投影,即可确定点A的三个坐标(x4,以,),然后按坐标值作 图。 作图:通常将轴测图上的X轴画成水平位置,Z轴画成铅垂位置,Y轴画成与X、Z轴成 135°,即与X轴延长线成45°。在相应轴上量取坐标x4、4、4,得到ax、a、a三点,然 后从这三点分别作各轴的平行线即得三个交点即为a、a、a,再从a、a、a作各轴的平 行线相交与一点,即得空间点A。 2.1.3两点的相对位置 1.两点的相对位置的确定空间点的位置可以用绝对坐标(即空间点对原点O的坐标) 来确定,也可以用相对于另一点的相对坐标来确定。两点的相对位置即为两点的坐标差。如 图2-9所示,己知空间点A(xA、4、三A)和B(x8、B、B),如分析B相对于A的位置,在 X方向相对坐标为(xB一x),即两点对W面,也就是左右方向的距离(横标)差。Y方向的 相对坐标为(g一%),即两点对V面,也就是前后方向的距离(纵标)差。Z方向的相对坐 标为(B一4),即两点对H面也就是高度方向的距离(高标)差。 b) 图2-9 两点的相对位置的确定 由于x>x,则(一x)为负值,即点A在左,点B在右。由于g>4,则(g一w) 为正值,即点B在前,点A在后。由于>,则(B一)为正值,即点B在上,点A在 下。 2.重影点的投影当两点的某两个坐标值相同时,该两点处于同一条投射线上,因而对 某一投影面具有重合的投影,这两点称为对该投影面的重影点。如图2-10所示C、D两点, 67
67 分析:根据点 A 的三面投影,即可确定点 A 的三个坐标(xA,yA,zA),然后按坐标值作 图。 作图:通常将轴测图上的 X 轴画成水平位置,Z 轴画成铅垂位置,Y 轴画成与 X、Z 轴成 135°,即与 X 轴延长线成 45°。在相应轴上量取坐标 xA、yA、zA,得到 ax、ay、az 三点,然 后从这三点分别作各轴的平行线即得三个交点即为 a、a'、a",再从 a、a'、a"作各轴的平 行线相交与一点,即得空间点 A。 2.1.3 两点的相对位置 1.两点的相对位置的确定 空间点的位置可以用绝对坐标(即空间点对原点 O 的坐标) 来确定,也可以用相对于另一点的相对坐标来确定。两点的相对位置即为两点的坐标差。如 图 2-9 所示,已知空间点 A(xA、yA、zA)和 B(xB、yB、zB),如分析 B 相对于 A 的位置,在 X 方向相对坐标为(xB-xA),即两点对 W 面,也就是左右方向的距离(横标)差。Y 方向的 相对坐标为(yB-yA),即两点对 V 面,也就是前后方向的距离(纵标)差。Z 方向的相对坐 标为(zB-zA),即两点对 H 面也就是高度方向的距离(高标)差。 W H V 后 前 下 上 左 右 下 上 左 右 后 前 b'' B A B B A A y y x x z z '' ' ' '' '' ' ' b A B b b b b O a a a YH X Yw Z O a a a Y Z X a) b) 图 2-9 两点的相对位置的确定 由于 xA>xB,则(xB-xA)为负值,即点 A 在左,点 B 在右。由于 yB>yA,则(yB-yA) 为正值,即点 B 在前,点 A 在后。由于 zB>zA,则(zB-zA)为正值,即点 B 在上,点 A 在 下。 2.重影点的投影 当两点的某两个坐标值相同时,该两点处于同一条投射线上,因而对 某一投影面具有重合的投影,这两点称为对该投影面的重影点。如图 2-10 所示 C、D 两点, X Z Y a x z y a a a a a X A A A Y Z X Y Z a a a A z a X a X y xA a O aY YH A aY YW a A aZ Z O O ' '' ' '' ' W '' H 45° a) b) c) 图 2-8 根据点的投影图画出轴测图