
一、在扩展域从描述和构成循环码 方法1:g()=LCM(mi,(),m2(☒,,mink) 方法2:直接由构造H。 在每个共扼根系选取一个共扼根(一般选次数最小的,计算简单),得 o1,c2,..,cw,构成H: (ai)"-1(a1)-2 a 1 (a)n-1(ah)"-2 ab H= (a)-1(a)n-2 ajm 把H中的o1,o2,..,ow转为m重,H仍有线性相关的行,在这些行中 保留一行,其余去掉
一、在扩展域从描述和构成循环码 方法1:g(x)=LCM (m i1 (x) , m i2 (x) ,…, m in-k (x) ) 方法2:直接由构造H。 在每个共扼根系选取一个共扼根(一般选次数最小的,计算简单),得 j1 , j2 ,…, jw , 构成H: = − − − − − − ) ) ....... 1 ....... ...... ...... ...... ...... ) ) ...... 1 ) ) ...... 1 H 1 2 1 2 1 2 2 2 2 1 1 1 w w w j n j n j j n j n j j n j n j ( ( ( ( ( ( 把H中的j1 , j2 ,…, jw转为m重,H仍有线性相关的行,在这些行中 保留一行,其余去掉
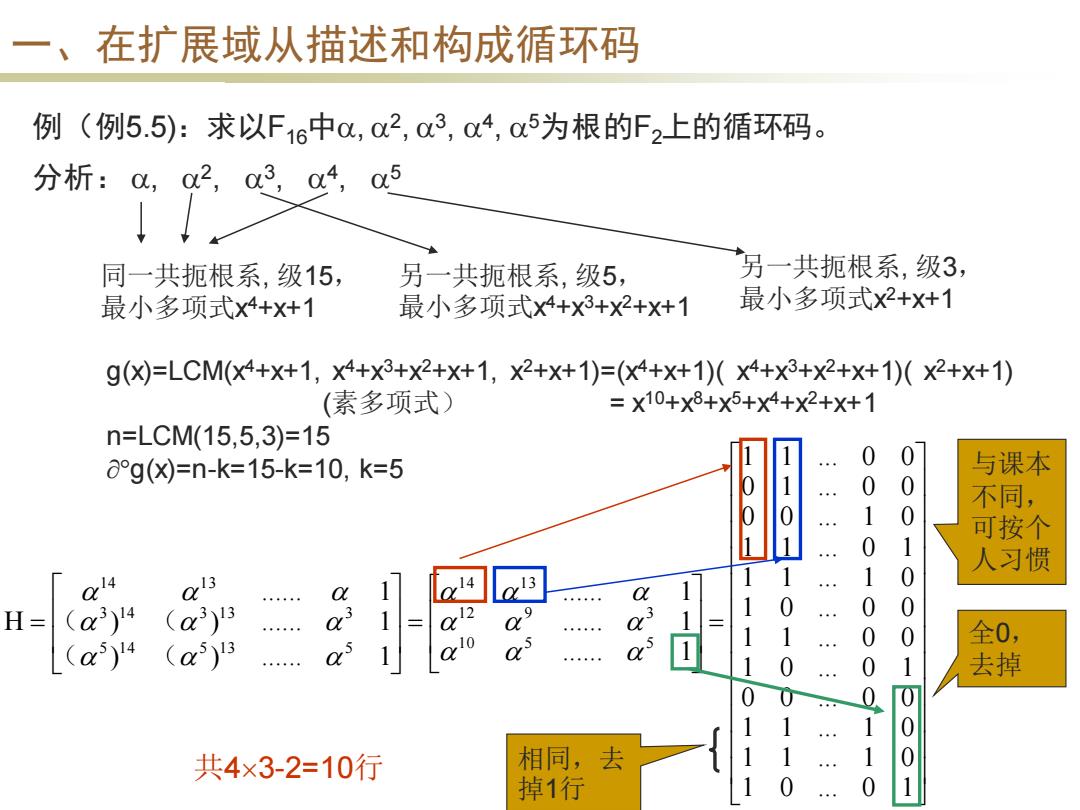
一 、在扩展域从描述和构成循环码 例(例5.5):求以F16中o,02,03,04,05为根的F2上的循环码。 分析:,2,34,5 同一共扼根系,级15, 另一共扼根系,级5, 另一共扼根系,级3, 最小多项式x4+x+1 最小多项式x4+x3+x2+x+1 最小多项式x2++1 g()=LCM(x4+X+1,X4+x3+x2+x+1,X2+X+1)=(X4+x+1)(x4+x3+x2+X+1)(X2+x+1) (素多项式) =X10+Xx8+x5+x4+x2+X+1 n=LCM(15,5,3)=15 ag(X)=n-k=15-k=10,k=5 0 0 与课本 0 0 不同, 1 0 可按个 0 人习惯 1 0 1 1 H= (a3)4 (a3)13 0 0 0 1 0 全0, (a5)14 (a5)3 as 1 0 a 1 1 0 0 1 去掉 0 0 1 1 8 共4×3-2=10行 相同,去 0 掉1行 1 0 1
一、在扩展域从描述和构成循环码 例(例5.5):求以F16中, 2 , 3 , 4 , 5为根的F2上的循环码。 分析: , 2 , 3 , 4 , 5 同一共扼根系, 级15, 最小多项式x 4+x+1 另一共扼根系, 级5, 最小多项式x 4+x3+x2+x+1 另一共扼根系, 级3, 最小多项式x 2+x+1 g(x)=LCM(x4+x+1, x4+x3+x2+x+1, x2+x+1)=(x4+x+1)( x4+x3+x2+x+1)( x2+x+1) (素多项式) = x10+x8+x5+x4+x2+x+1 n=LCM(15,5,3)=15 g(x)=n-k=15-k=10, k=5 = = = 1 0 ... 0 1 1 1 ... 1 0 1 1 ... 1 0 0 0 ... 0 0 1 0 ... 0 1 1 1 ... 0 0 1 0 ... 0 0 1 1 ... 1 0 1 1 ... 0 1 0 0 ... 1 0 0 1 ... 0 0 1 1 ... 0 0 ...... 1 ...... 1 ...... 1 ) ) ...... 1 ) ) ...... 1 ...... 1 H 1 0 5 5 1 2 9 3 1 4 1 3 5 1 4 5 1 3 5 3 1 4 3 1 3 3 1 4 1 3 ( ( ( ( 与课本 不同, 可按个 人习惯 全0, 去掉 相同,去 掉1行 共43-2=10行

二、二进制BCH码 若g(X)在扩展域Fqm上的根为c1,o2,,0n-k,则 「(a4)-1( a4)"-2 a H= (a2)-1(a2)-2 a 1 (a)n-(a)n-2 an-k 若i1,2,ink中含有1,2,…,d-1,则抽这d-1行和任意d-1列,得 ai- (a2) (a-i)h (a)k (aa-la 每一列提取公因式,得 H=ai+ja+.+jd ah - =a+j++j (aa) ()-2(a-2 (a)4-2 d-2>ju>jv2l
二、二进制BCH码 若g(x)在扩展域Fqm上的根为i1 , i2 ,…, in-k,则 = − − − − − − − − − ) ) ....... 1 ....... ...... ...... ...... ...... ) ) ...... 1 ) ) ...... 1 H 1 2 1 2 1 2 2 2 2 1 1 1 n k n k n k i n i n i i n i n i i n i n i ( ( ( ( ( ( 若i1 ,i2 ,…, in-k中含有1,2,…,d-1, 则抽这d-1行和任意d-1列,得 1 2 1 1 2 1 1 2 1 ) ) ....... ( ) ....... ...... ...... ...... ) ) ...... ( ) ...... 1 1 1 2 2 2 − − − − − − d d d d j d j d j j j j j j j ( ( ( ( 每一列提取公因式,得 − + + + − − − + + + = = − − − − − 2 1 ... 2 2 2 ... ( ) ) ) ....... ) ....... ...... ...... ...... ...... 1 1 ...... 1 H 1 2 1 1 2 1 1 2 1 1 2 1 u v d u v d d d d j j j j j j j j d j d j d j j j j j j ( ( (
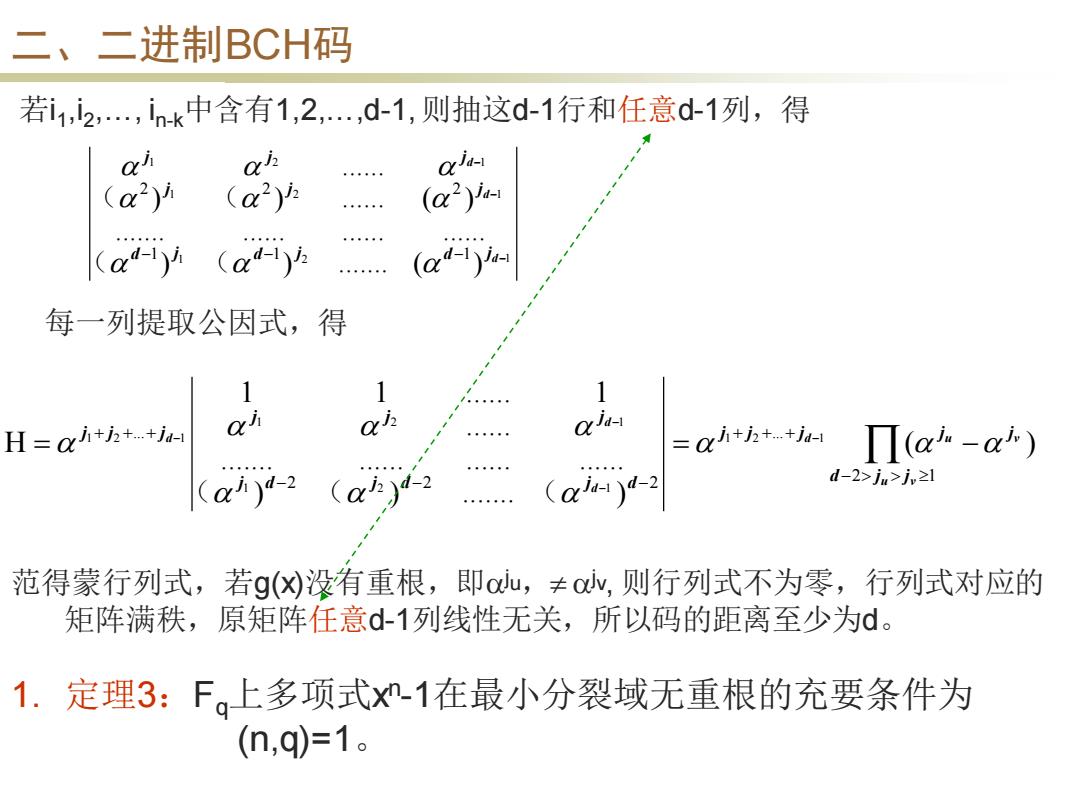
二、二进制BCH码 若i1,2,,ink中含有1,2…,d-1,则抽这d-1行和任意d-1列,得 a ) - (a2)y (a)h (a): (a4-1) 每一列提取公因式,得 1 H=a+j2+.+ju- =atatt Π(a.-a) ()-2 ( (aa)4-2 d-2>ju>jvzl 范得蒙行列式,若g(没有重根,即o,≠o,则行列式不为零,行列式对应的 矩阵满秩,原矩阵任意d-1列线性无关,所以码的距离至少为d。 1.定理3:F。上多项式xn1在最小分裂域无重根的充要条件为 (n,q)=1
二、二进制BCH码 若i1 ,i2 ,…, in-k中含有1,2,…,d-1, 则抽这d-1行和任意d-1列,得 1 2 1 1 2 1 1 2 1 ) ) ....... ( ) ....... ...... ...... ...... ) ) ...... ( ) ...... 1 1 1 2 2 2 − − − − − − d d d d j d j d j j j j j j j ( ( ( ( 每一列提取公因式,得 − + + + − − − + + + = = − − − − − 2 1 ... 2 2 2 ... ( ) ) ) ....... ) ....... ...... ...... ...... ...... 1 1 ...... 1 H 1 2 1 1 2 1 1 2 1 1 2 1 u v d u v d d d d j j j j j j j j d j d j d j j j j j j ( ( ( 范得蒙行列式,若g(x)没有重根,即ju, jv , 则行列式不为零,行列式对应的 矩阵满秩,原矩阵任意d-1列线性无关,所以码的距离至少为d。 1. 定理3:Fq上多项式x n -1在最小分裂域无重根的充要条件为 (n,q)=1