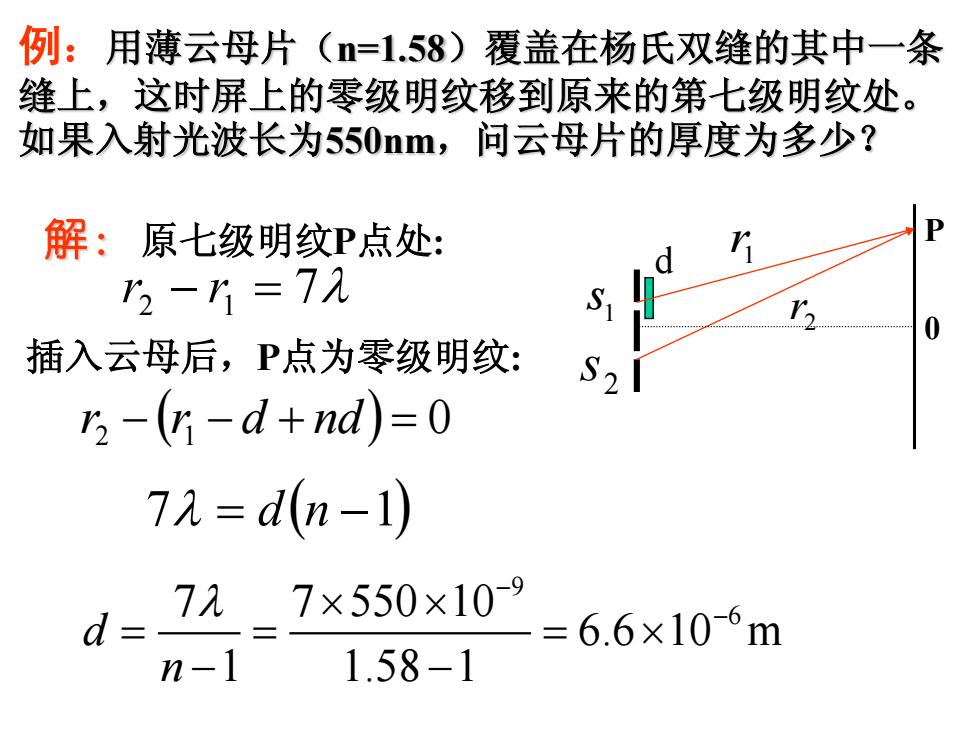
例:用薄云母片(n=1.58)覆盖在杨氏双缝的其中一条 缝上,这时屏上的零级明纹移到原来的第七级明纹处。 如果入射光波长为550nm,问云母片的厚度为多少? 解:原七级明纹P点处: 3-1=7九 插入云母后,P点为零级明纹: S 2 3-(-d+nd)=0 7=d(n-1) d= 7元7×550×109 =6.6×10-6m n-1 1.58-1
例:用薄云母片(n=1.58)覆盖在杨氏双缝的其中一条 缝上,这时屏上的零级明纹移到原来的第七级明纹处。 如果入射光波长为550nm,问云母片的厚度为多少? 解: 原七级明纹P点处: r2 r1 7 插入云母后,P点为零级明纹: 0 r2 r1 d nd 7 dn 1 9 7 7 550 10 6 6.6 10 m 1 1.58 1 d n P 0 1 r 2 r d 1 s 2 s

例:一射电望远镜的天线设在湖岸上,距湖面高度为,对 岸地平线上方有一恒星正在升起,恒星发出波长为的电磁波。 求:当天线测得第1级干涉极大时恒星所在的角位置。 解: 由几何关系,并考 虑到在水面反射时 存在着半波损失 6=AC-BC士 2 AC-BC= (1-cos2a)=2hsina sina δ=2 hsina± 2 0 2 32 a arcsin a2 arcsin 4h 4h
2 AC BC (1 cos2 ) 2 sin sin h h AC BC 2 0 2 sin h 4h 1 arcsin 4h 3 2 arcsin 例:一射电望远镜的天线设在湖岸上,距湖面高度为h,对 岸地平线上方有一恒星正在升起,恒星发出波长为的电磁波。 求:当天线测得第1级干涉极大时恒星所在的角位置。 h C A B 2 解: 由几何关系,并考 虑到在水面反射时 存在着半波损失
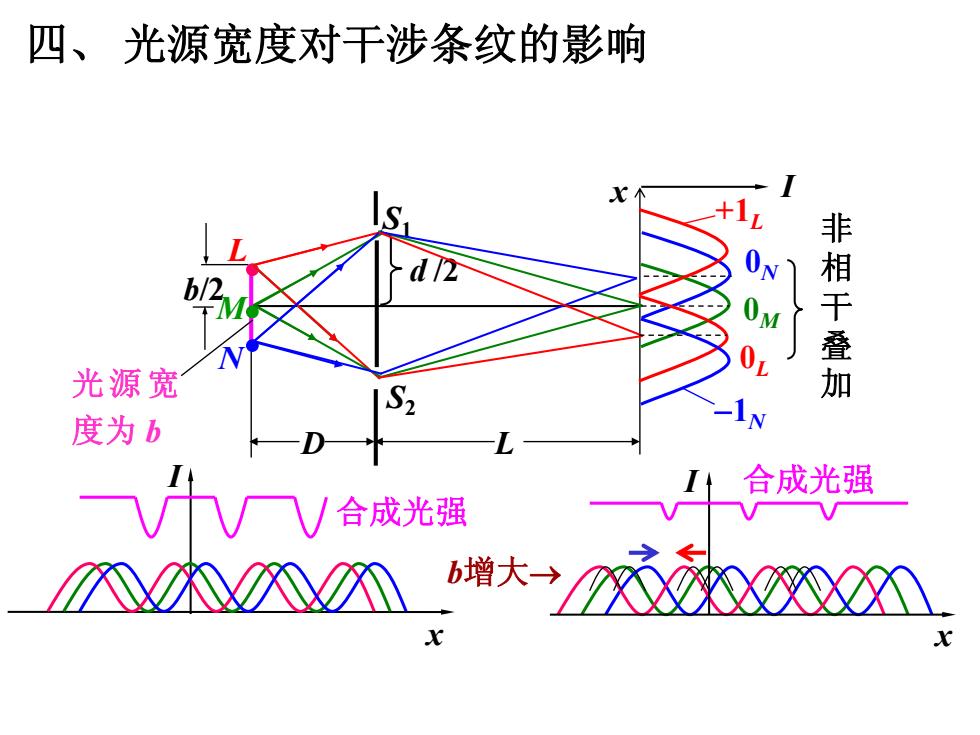
四、光源宽度对干涉条纹的影响 UN 0 非相干叠加 光源宽 度为b 合成光强 /合成光强 增大→0XX①
S1 d /2 S2 D L 光源宽 度为 b b/2 L M N 0M 0N 0L I 非 相 干 叠 加 +1L 1N x I 合成光强 I x 合成光强 b增大 四、 光源宽度对干涉条纹的影响 x
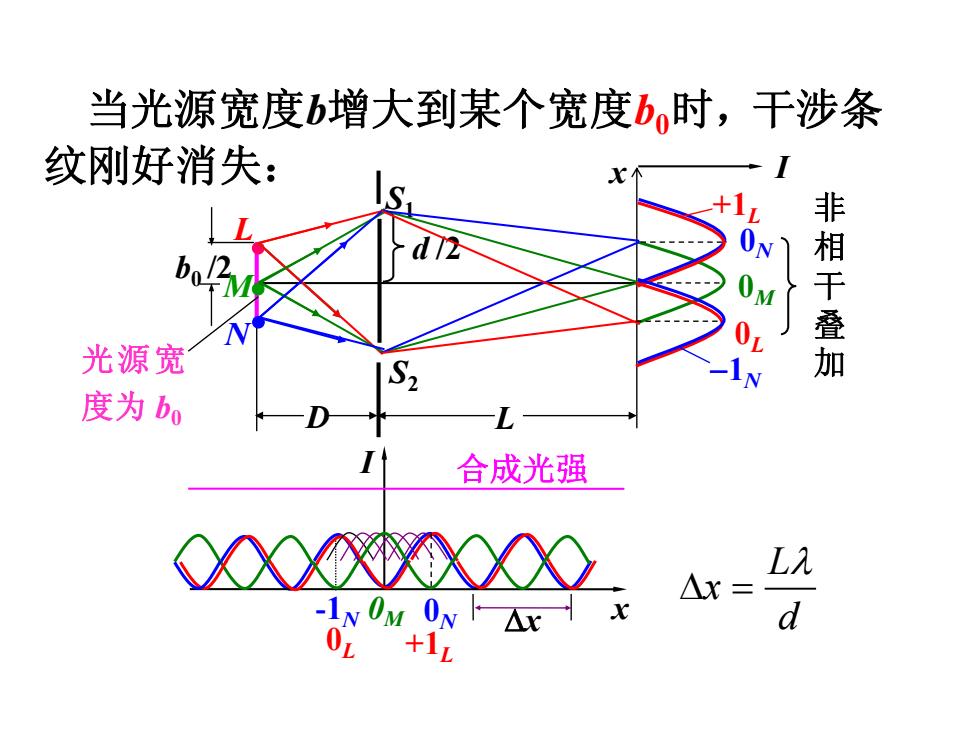
当光源宽度b增大到某个宽度b时,干涉条 纹刚好消失: 非相干叠加 光源宽 度为ba 合成光强 XX☒X0 L入 Ar= -IN OM ON Ax d 02+17
L x d x I 合成光强 0N x +1L 0M 0L -1N S1 d /2 S2 D L 光源宽 度为 b0 b0 /2 L M N 0M 0N 0L I 非 相 干 叠 加 +1L 1N 当光源宽度b增大到某个宽度b0时, 纹刚好消失: 干涉条 x
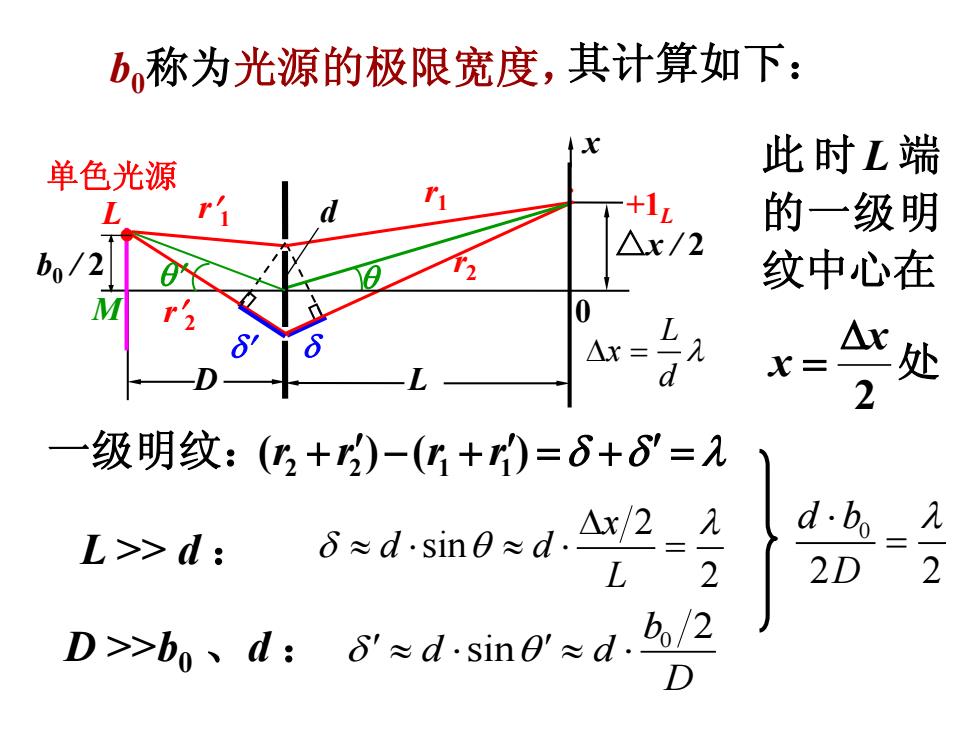
b称为光源的极限宽度,其计算如下: 单色光源 此时L端 +1 的一级明 △/2 b/2 纹中心在 △x= △X x= 处 2 级明纹:(3+)-(+)=δ+8=九 d≈d.sin≈d.Ar/2 λ d.bo L>>d: 2 2D 2 D>b、d:6≈d-sine≈d.b/2
(r2 r2 )(r1 r1 ) 0 2 sin b d d D 2 sin 2 x d d L L >> d : D >>b0 、d : b0称为光源的极限宽度, L x d △x / 2 r 1 +1L d 0 D L · r2 r1 r 2 单色光源 b0 / 2 x L M 0 2 2 d b D 其计算如下: 此 时 L 端 的一级明 纹中心在 处 2 x x 一级明纹: