二、定常约束与非定常约束 约束条件不随时间变化的约束称为定常约束。 约束条件随时间变化的约束称为非定常约束。 X 其约束方程为 x2+y2=(-ut)2 OM(x,y)
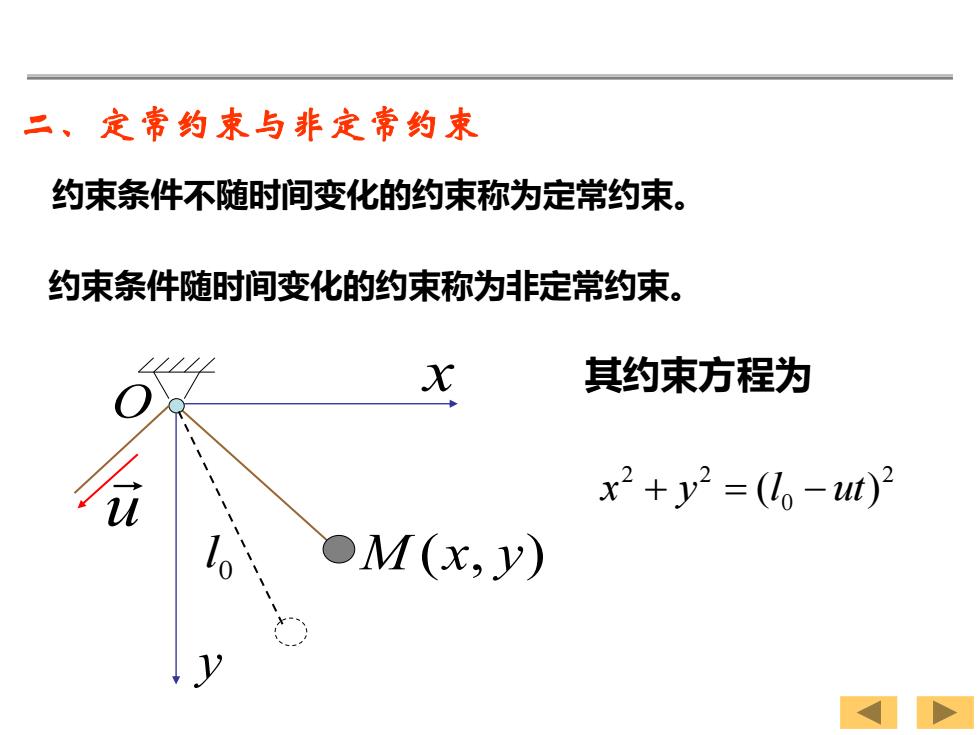
二、定常约束与非定常约束 约束条件不随时间变化的约束称为定常约束。 约束条件随时间变化的约束称为非定常约束。 O x y M (x, y) u 0 l 其约束方程为 2 0 2 2 x + y = (l −ut)

非定常约束方程的一般形式为 f(X1,乃1,21,.,Xn,yn,2n,t)=0 三、双面约束与单面约束 同时限制质点某方向及相反方向运动的约束称为双面约 束。 只能限制质点某方向的运动,而不能限制相反方向运动 的约束称为单面约束。其约束方程的一般形式为 f(X1,1,21,.,Xn,yn,2n)<0
非定常约束方程的一般形式为 f r (x1 , y1 ,z1 , , xn , yn ,zn ,t) = 0 三、双面约束与单面约束 同时限制质点某方向及相反方向运动的约束称为双面约 束。 只能限制质点某方向的运动,而不能限制相反方向运动 的约束称为单面约束。其约束方程的一般形式为 f r (x1 , y1 ,z1 , , xn , yn ,zn ) 0

四、完整约束与非完整约束 几何约束或其约束方程能够积分的运动约束称为 完整约束。 如果在约束方程中显含坐标对时间的导数,并且 不可以积分,这种约束称为非完整约束。 本章只研究定常的双面的完整的几何约束问题
四、完整约束与非完整约束 几何约束或其约束方程能够积分的运动约束称为 完整约束。 如果在约束方程中显含坐标对时间的导数,并且 不可以积分,这种约束称为非完整约束。 本章只研究定常的双面的完整的几何约束问题

虚位移原理 、 虚位移的概念 在某瞬时,质点系在约束允许的条件下,可能实 现的任何微小的位移,称为该质点系的虚位移。如 M(x,y)
一、虚位移的概念 在某瞬时,质点系在约束允许的条件下,可能实 现的任何微小的位移,称为该质点系的虚位移。如 O x y M (x, y) r O A B x y A r B r 虚位移原理

必须指出,虚位移和实位移都受约束的限制,是 约束所允许的位移,但二者是有区别的。实位移是在 一定的力作用下和给定的运动初始条件下,在一定的 时间内发生的位移,具有确定的方向,可能是微小值 也可能是有限值。而虚位移纯粹是一个几何概念,它 既不牵涉到系统的实际运动,也不涉及到力的作用, 与时间过程和运动的初始条件无关,它一定是微小值 在约束允许的条件下具有任意性。一个静止的质点或 质点系不会发生实位移,但可以有虚位移。在定常约 束的情况下,微小实位移必定是虚位移中的一个。在 非定常约束的情况下,实位移与虚位移没有关系
必须指出,虚位移和实位移都受约束的限制,是 约束所允许的位移,但二者是有区别的。实位移是在 一定的力作用下和给定的运动初始条件下,在一定的 时间内发生的位移,具有确定的方向,可能是微小值, 也可能是有限值。而虚位移纯粹是一个几何概念,它 既不牵涉到系统的实际运动,也不涉及到力的作用, 与时间过程和运动的初始条件无关,它一定是微小值, 在约束允许的条件下具有任意性。一个静止的质点或 质点系不会发生实位移,但可以有虚位移。在定常约 束的情况下,微小实位移必定是虚位移中的一个。在 非定常约束的情况下,实位移与虚位移没有关系