
图58变角度空间桁架模型 a计算模型示意图b)环向剪力流©)内力平衡图 变角度空间桁架模型的基本假定有: (1)混凝土只承受压力,具有螺旋形裂缝的混凝土外壳组成桁架的斜压杆,其倾角为α: (2)纵筋和箍筋只承受拉力,分别构成桁架的弦杆和煦杆: (3)忽略核心混凝土的抗扭作用和钢筋的销栓作用 在上述假定中,忽略核心混凝士的抗扭作用的假定更为重要。这样,实心截面构件可以 看作为一箱形截面构件或一薄壁管构件,从而在受扭承载力计算中,可应用薄壁管理论。 由薄壁管理论,在扭矩T作用下,沿箱形截面侧壁中将产生大小相同的环向剪力流q, 如图5-8b)所示,且由图可得到 q=1=2 (5-4) 式中A一一剪力流路线所围成的面积,此处取为构件核心截面积即箍筋内表面所围成的 面积: T 一扭矩产生的剪应力: 箱形碱面侧壁厚度。 图5-8c)所示为作用于侧壁的剪力流g引起的桁架各杆件的内力图,其中α为斜压杆的 倾角,为单肢箍筋拉力总和,F为纵筋拉力总和,D为混凝土斜压杆轴压力之和。由图 示力学平衡条件可得到 N=F.tand (5-5) 在极限状态下: N=24mh cota24bo cota Am2(+)cota 6
5-6 ) ) ) 图 5-8 变角度空间桁架模型 a)计算模型示意图 b)环向剪力流 c)内力平衡图 变角度空间桁架模型的基本假定有: (1)混凝土只承受压力,具有螺旋形裂缝的混凝土外壳组成桁架的斜压杆,其倾角为 ; (2)纵筋和箍筋只承受拉力,分别构成桁架的弦杆和腹杆; (3)忽略核心混凝土的抗扭作用和钢筋的销栓作用。 在上述假定中,忽略核心混凝土的抗扭作用的假定更为重要。这样,实心截面构件可以 看作为一箱形截面构件或一薄壁管构件,从而在受扭承载力计算中,可应用薄壁管理论。 由薄壁管理论,在扭矩 Tu 作用下,沿箱形截面侧壁中将产生大小相同的环向剪力流 q , 如图 5-8b)所示,且由图可得到 2 u cor T q t A = = (5-4) 式中 Acor ——剪力流路线所围成的面积,此处取为构件核心截面积,即箍筋内表面所围成的 面积; ——扭矩产生的剪应力; t ——箱形截面侧壁厚度。 图 5-8c)所示为作用于侧壁的剪力流 q 引起的桁架各杆件的内力图,其中 为斜压杆的 倾角, N 为单肢箍筋拉力总和, F 为纵筋拉力总和,D为混凝土斜压杆轴压力之和。由图 示力学平衡条件可得到 N F= tan (5-5) 在极限状态下: ( ) 1 1 1 cot cot 2 2 2 cot sv sv cor sv sv cor v v sv sv cor cor v A f h A f b N S S A f h b S = + + =
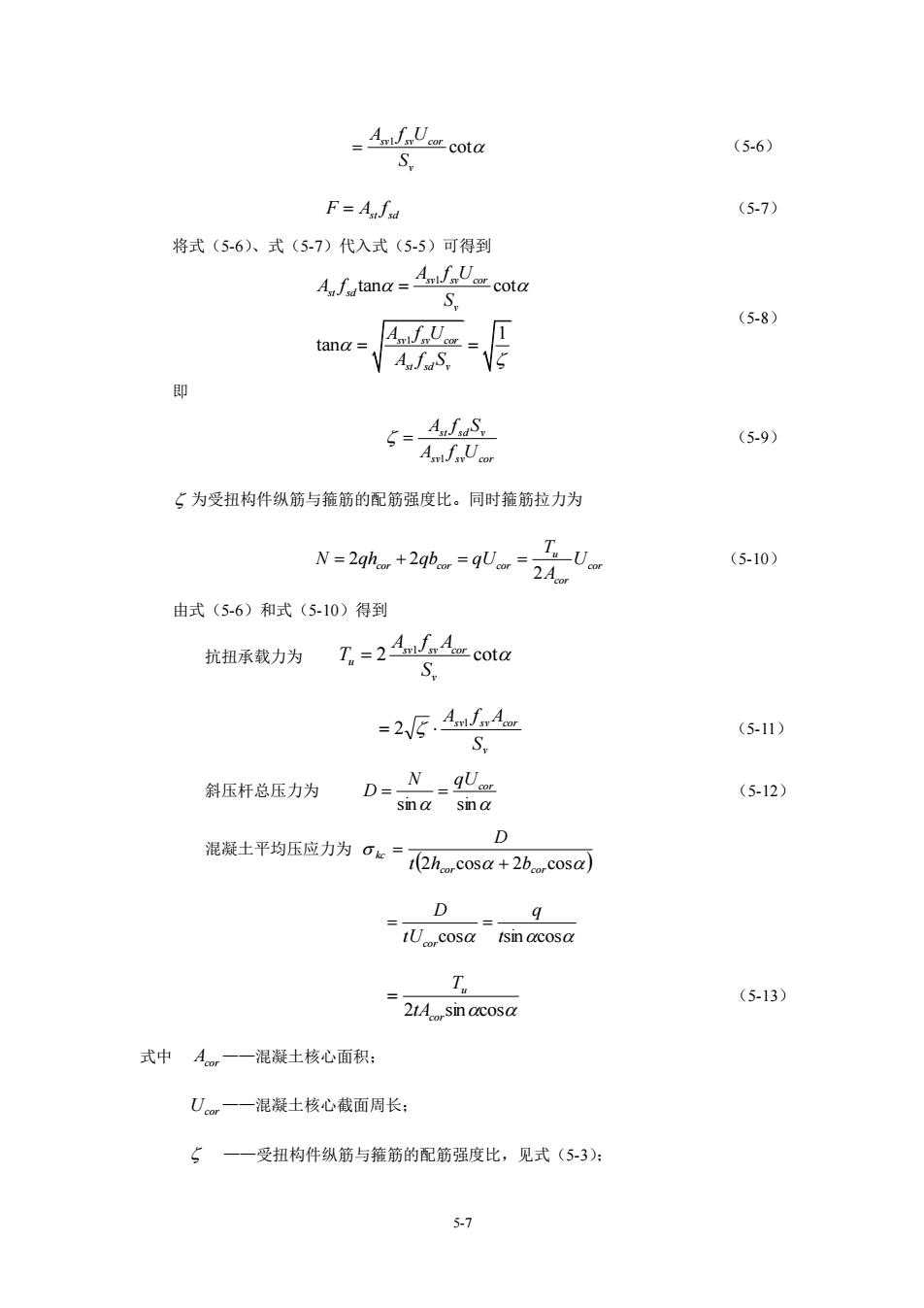
Amf.U cota (5-6) F=A∫a 5 将式(5-6)、式(5-7)代入式(5-5)可得到 A/aamw=4a人L_cota 恶 50 AmfUcor 二为受扭构件纵筋与箍筋的配筋强度比。同时箍筋拉力为 T N=2g+2g0.=g02元 (5.10) 由式(5-6)和式(5-10)得到 抗扭承载力为T.=24m人4cota S -2VE.AA s, 斜压杆总压力为 D= 混凝士平均压应力为0s-亿hc0sa+2hc0sa D cos sin acosa T 21Asin ccosa 式中A一一混凝土核心面积: U一一混凝士核心截面周长 5一—受扭构件纵筋与箍筋的配筋强度比,见式(5-3): 5-7
5-7 1 cot sv sv cor v A f U S = (5-6) st sd F = A f (5-7) 将式(5-6)、式(5-7)代入式(5-5)可得到 1 1 tan cot 1 tan sv sv cor st sd v sv sv cor st sd v A f U A f S A f U A f S = = = (5-8) 即 sv sv cor st sd v A f U A f S 1 = (5-9) 为受扭构件纵筋与箍筋的配筋强度比。同时箍筋拉力为 2 2 2 u cor cor cor cor cor T N qh qb qU U A = + = = (5-10) 由式(5-6)和式(5-10)得到 抗扭承载力为 1 2 cot sv sv cor u v A f A T S = v sv sv cor S A 1 f A = 2 (5-11) 斜压杆总压力为 sin sin N qUcor D = = (5-12) 混凝土平均压应力为 ( ) 2 cos 2 cos cor cor kc t h b D + = cos tsincos q tU D cor = = 2 corsincos u tA T = (5-13) 式中 Acor ——混凝土核心面积; Ucor ——混凝土核心截面周长; ——受扭构件纵筋与箍筋的配筋强度比,见式(5-3);

A,—纯扭计算中沿截面周边对称配置的全部纵向钢筋截面积: A一一箍筋单肢面积: S,一抗扭箍筋间距: ∫。一抗扭纵筋抗拉强度设计值: ∫,一一抗扭筘筋抗拉强度设计值。 由式(5-11)可以看出,构件的扭矩承载力T,主要与钢筋骨架尺寸、箍筋用量及其强度, 以及表征纵筋与箍筋的相对用量的参数5有关。按照变角度空间桁架模型,不仅有如式 (5-9)的物理意义,而且有如公式(58)所示表征斜压杆倾角α的大小,因而在计算模 型中还具有一定的几何意义。 式(51)为低配筋受扭构件扭矩承载力的计算公式。为了保证钢筋应力达到屈服强度 前不发生混凝士压坏,即避免出现超筋构件的脆性破坏,必须限制按公式(5-13)计算得到 的斜压杆平均应力σ的大小。 2)斜弯曲破坏理论(亦称扭曲破坏面极限平衡理论) 斜弯曲破坏理论是以实验为基础的。对于纯扭的钢筋混凝土构件,在扭矩作用下,构件 总是在己经形成螺旋形裂缝的某一最薄弱的空间曲面发生破坏。如图5-9所示,AB、BC、 CD、为三段连续的斜向破坏裂缝,其与构件纵轴线方向的夹角为α。AD段为倾斜压区。斜 弯曲破坏理论乃是截取实际的破坏面作为隔离体,从而直接导出与纵筋、箍筋用量有关的抗 扭承载力计算公式的。 斜弯曲计算理论的基本假定为: (1)假定通过扭曲裂面的纵向钢筋、箍筋在构件破坏时均已达到其屈服强度: (2)受压区高度近似地取为两倍的保护层厚度,即受压区重心正位于箍筋处。假定受 压区的合力近似地作用于受压区的形心: (3)混凝土的抗扭能力忽略不计,扭矩全部由抗扭纵筋和箍筋承担: (4)假定抗扭纵筋沿构件核心周边对称、均匀布置,抗扭箍筋沿构件轴线方向等距离 布置,且均错固可靠。 根据以上基本假定,令通过受压区形心而平行于构件纵向中心轴x的轴为H轴,由对 该轴的内外扭矩的静力平衡条件可得到 58
5-8 Ast ——纯扭计算中沿截面周边对称配置的全部纵向钢筋截面积; Asv1——箍筋单肢面积; v S ——抗扭箍筋间距; sd f ——抗扭纵筋抗拉强度设计值; sv f ——抗扭箍筋抗拉强度设计值。 由式(5-11)可以看出,构件的扭矩承载力 Tu 主要与钢筋骨架尺寸、箍筋用量及其强度, 以及表征纵筋与箍筋的相对用量的参数 有关。按照变角度空间桁架模型, 不仅有如式 (5-9)的物理意义,而且有如公式(5- 8 )所示表征斜压杆倾角 的大小,因而在计算模 型中还具有一定的几何意义。 式(5-11)为低配筋受扭构件扭矩承载力的计算公式。为了保证钢筋应力达到屈服强度 前不发生混凝土压坏,即避免出现超筋构件的脆性破坏,必须限制按公式(5-13)计算得到 的斜压杆平均应力 kc 的大小。 2)斜弯曲破坏理论(亦称扭曲破坏面极限平衡理论) 斜弯曲破坏理论是以实验为基础的。对于纯扭的钢筋混凝土构件,在扭矩作用下,构件 总是在已经形成螺旋形裂缝的某一最薄弱的空间曲面发生破坏。如图 5-9 所示,AB、BC、 CD、为三段连续的斜向破坏裂缝,其与构件纵轴线方向的夹角为 。AD 段为倾斜压区。斜 弯曲破坏理论乃是截取实际的破坏面作为隔离体,从而直接导出与纵筋、箍筋用量有关的抗 扭承载力计算公式的。 斜弯曲计算理论的基本假定为: (1)假定通过扭曲裂面的纵向钢筋、箍筋在构件破坏时均已达到其屈服强度; (2)受压区高度近似地取为两倍的保护层厚度,即受压区重心正位于箍筋处。假定受 压区的合力近似地作用于受压区的形心; (3)混凝土的抗扭能力忽略不计,扭矩全部由抗扭纵筋和箍筋承担; (4)假定抗扭纵筋沿构件核心周边对称、均匀布置,抗扭箍筋沿构件轴线方向等距离 布置,且均锚固可靠。 根据以上基本假定,令通过受压区形心而平行于构件纵向中心轴 x 的轴为 I-I 轴,由对 该轴的内外扭矩的静力平衡条件可得到