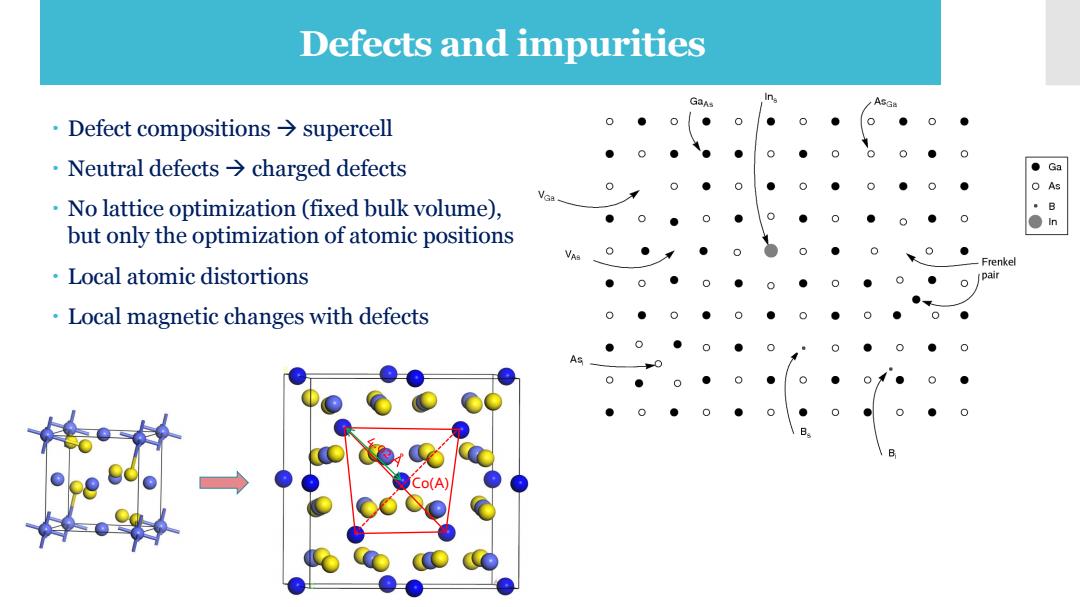
Defects and impurities GaAs ASGa ·Defect compositions→supercell 0●0 ● ● ● ●0 ·Neutral defects→charged defects ●Ga As No lattice optimization (fixed bulk volume), ●0 ● ●n but only the optimization of atomic positions ●) Frenkel Local atomic distortions (pair Local magnetic changes with defects 0
Defects and impurities Co(A) Defect compositions → supercell Neutral defects → charged defects No lattice optimization (fixed bulk volume), but only the optimization of atomic positions Local atomic distortions Local magnetic changes with defects
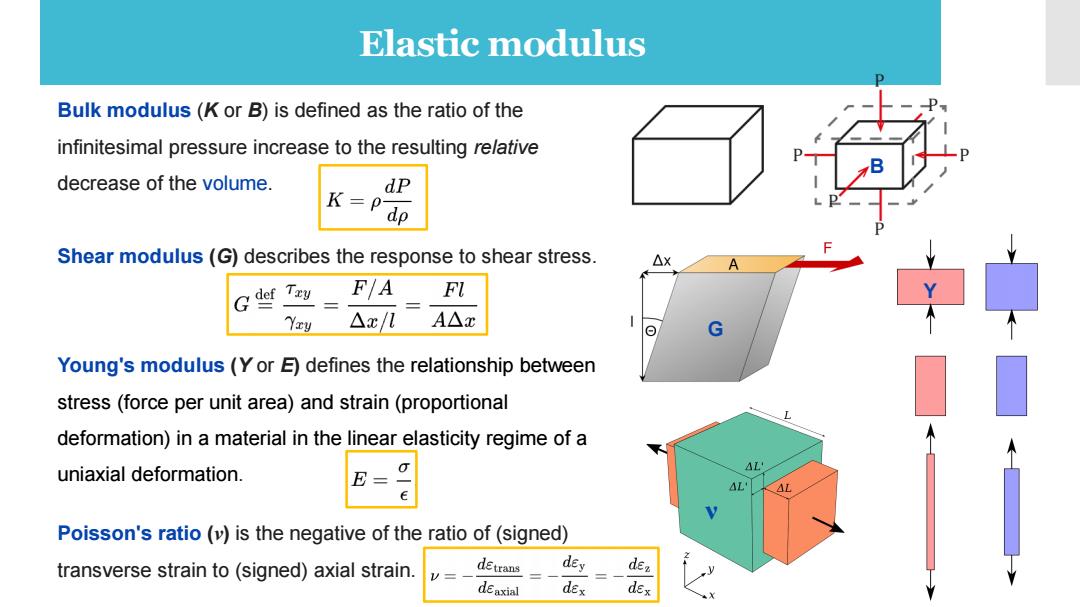
Elastic modulus Bulk modulus(K or B)is defined as the ratio of the infinitesimal pressure increase to the resulting relative decrease of the volume. dP K=P dp Shear modulus(G)describes the response to shear stress. △X G def Tzy FA Fl Yay △x/U A△x Young's modulus (Y or E)defines the relationship between stress(force per unit area)and strain(proportional deformation)in a material in the linear elasticity regime of a uniaxial deformation. AL' AL Poisson's ratio(v)is the negative of the ratio of(signed) transverse strain to(signed)axial strain. V= detrans dey dez deaxial dex dex
Elastic modulus Bulk modulus (K or B) is defined as the ratio of the infinitesimal pressure increase to the resulting relative decrease of the volume. Shear modulus (G) describes the response to shear stress. Young's modulus (Y or E) defines the relationship between stress (force per unit area) and strain (proportional deformation) in a material in the linear elasticity regime of a uniaxial deformation. Poisson's ratio (ν) is the negative of the ratio of (signed) transverse strain to (signed) axial strain. B G ν Y

K- E= 入= G- V= M= (K,E) 3K(3K-E) 3KE 3K-E 3K(3K+E) 9K-E 9K-E 6K 9K-E (K,) 9K(K-X) 3(K-) 3K-2λ 3K- 2 3K- (K,G) 9KG 3K-2G 3K+G K-9 23K+G) K+9 (K,) 3K(1-2w) 3Kv 3K1-2w) 3K(1-) Bulk modulus(灯 1+0 21+) 1+形 (K,M) 9K(M-K) 3K-M 3(M-K) 3K-M Shear modulus(G) 3K+M 4 3K+M (E,) E+3A+R E-3A+R 2A E-A+R Young's modulus (E) 6 4 EHA+R 2 (E,G) EG G(E-2G) G(4G-E) 3(3G-E 易-1 Poisson's ratio (v) 3G-E 3G-E E Ev (E,w) E E(1-w) 3(1-2) (1+w)(1-2) 21+) Lame's first parameter (4) (1+w1-2) P-wave modulus (M) (E,M) 3M-E+S M-E+S 3M+E-S E-M+S 6 4 8 4M Homogeneous isotropic linear elastic materials have their (入,G) A+婴 G3入+2G) 入 入+2G λ+G 2(A+G) elastic properties uniquely (A,) (1+ A(1+w)1-2w) A1-2)) A(1- 3 2v determined by any two moduli (A,M) M+2X (M-A(M+2A) M-X 3 M+λ 2 among these;thus,given any (G,) 2G1+w) 31-2) 2G1+w) 2Gv 2G1-) 1-2 two,any other of the elastic 1-2w (G,M) M-9 G(3M-4G) M-2G M-2G moduli can be calculated M-G 2M-2G (w,M) M1+) M(1+01-2) Mv M(1-2) according to these formulas. 3(1-) 1- 1-2 2(1-)
Elastic modulus Homogeneous isotropic linear elastic materials have their elastic properties uniquely determined by any two moduli among these; thus, given any two, any other of the elastic moduli can be calculated according to these formulas. Bulk modulus (K) Shear modulus (G) Young's modulus (E) Poisson's ratio (ν) Lamé's first parameter (λ) P-wave modulus (M)

INSTTTUTE OF PHYSICS PUBLISHENG Elastic modulus J.Phys.:Condens.Matter 15 (2003)5307-5314 PLS953-898403162293-9 The elastic energy of a solid under strain is given by Ab initio elastic constants for the lonsdaleite phases of C,Si and Ge V 6 6 △E= SQ Wang and H Q Ye! Cijeiej GPa GPa Nb A-0.5 Fe A-2.4 150 V is the volume of the undistorted lattice cell,E is the energy 140 130 increment from the strain with vector e=(e,e2,e3,e,es,e6) 100 20 0 200 C is the matrix of the elastic constants. 100 100 100 0 100 100 160 For cubic phases--three independent elastic constants,Cu,C2 and C4; -100 0 0 100 -100 000 -100 100 140 For hexagonal phases--two more independent elastic constants,C13 and C33. The primitive vectors of a cubic diamond structure are defined as 一2 245 .(I+e) 0 22 学 22
Elastic modulus The elastic energy of a solid under strain is given by V is the volume of the undistorted lattice cell, E is the energy increment from the strain with vector e = (e1 , e2 , e3 , e4 , e5 , e6 ). C is the matrix of the elastic constants. For cubic phases -- three independent elastic constants, C11, C12 and C44; For hexagonal phases -- two more independent elastic constants, C13 and C33. The primitive vectors of a cubic diamond structure are defined as