
注意: 等效只是针对外电路而言, 对其内部电路是不等效的。 52 2 对外等效,但内 部电流不等效 对外等效,但内部电压不等效 应用电路等效变换的方法分析电路时,只可用变换后 的电路求解外部电路的电压、电流;求解内部电路的电压 电流时要在原电路中求解
注意: 等效只是针对外电路而言, 对其内部电路是不等效的。 2Ω 2Ω i u 1Ω i u 对外等效,但内 部电流不等效 对外等效,但内部电压不等效 应用电路等效变换的方法分析电路时,只可用变换后 的电路求解外部电路的电压、电流;求解内部电路的电压、 电流时要在原电路中求解。 5Ω u i S i i i S u
§2-31 电阻的串联和并 联 R R2 0 R=R1+R2 ul 1W2 u u R一U U=R+R2 U2- R2 U R1+R2 RR2 B21 R1+R2 L=R+Ri 或:G=G1+G2 式中G、G1、G2为R、R1、R2的 电导,G的单位为:西门子S
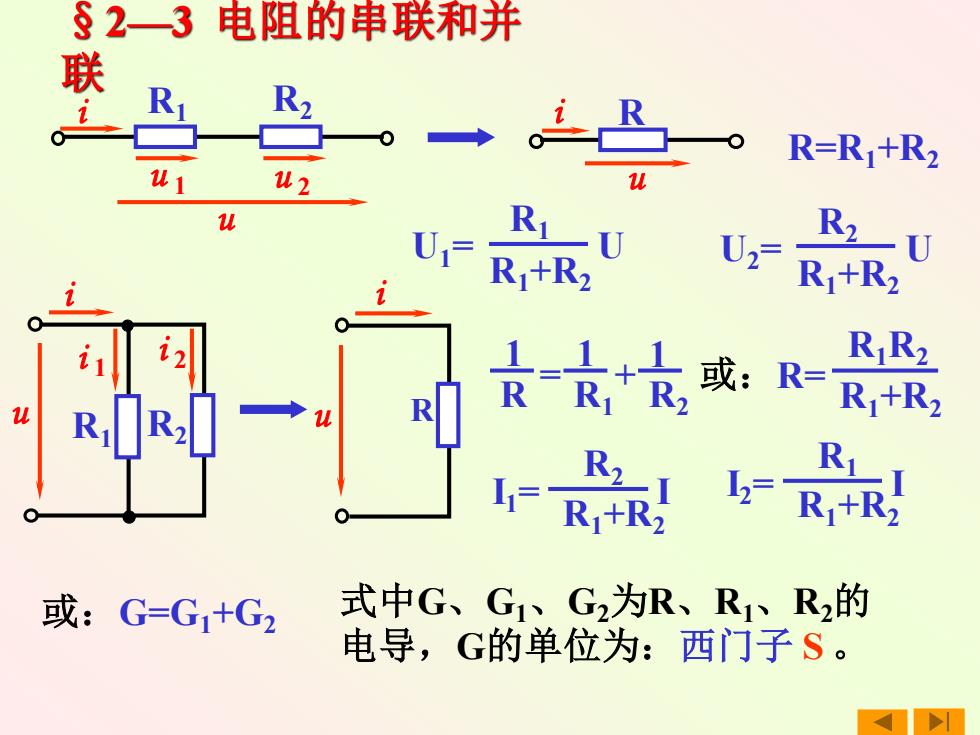
§2—3 电阻的串联和并 联 R=R1+R2 U1= U R1+R2 R1 u R1 i R i R2 u 1 u 2 u u i i 1 i 2 R1 R2 u R i 1 R = 1 R1 + 1 R2 或:R= R1+R2 R1R2 或:G=G1+G2 I1= I R1+R2 R2 式中G、G1、G2为R、R1、R2的 电导,G的单位为:西门子 S 。 U2= U R1+R2 R2 I2= I R1+R2 R1
等电位点的概念: .Ua=Ub b a ∴.a、 b为自 2R 2R 然等电位点 2R 2R 可见:自然等电 (Duab 位点之间可以看 成短路,也可以 看成断路
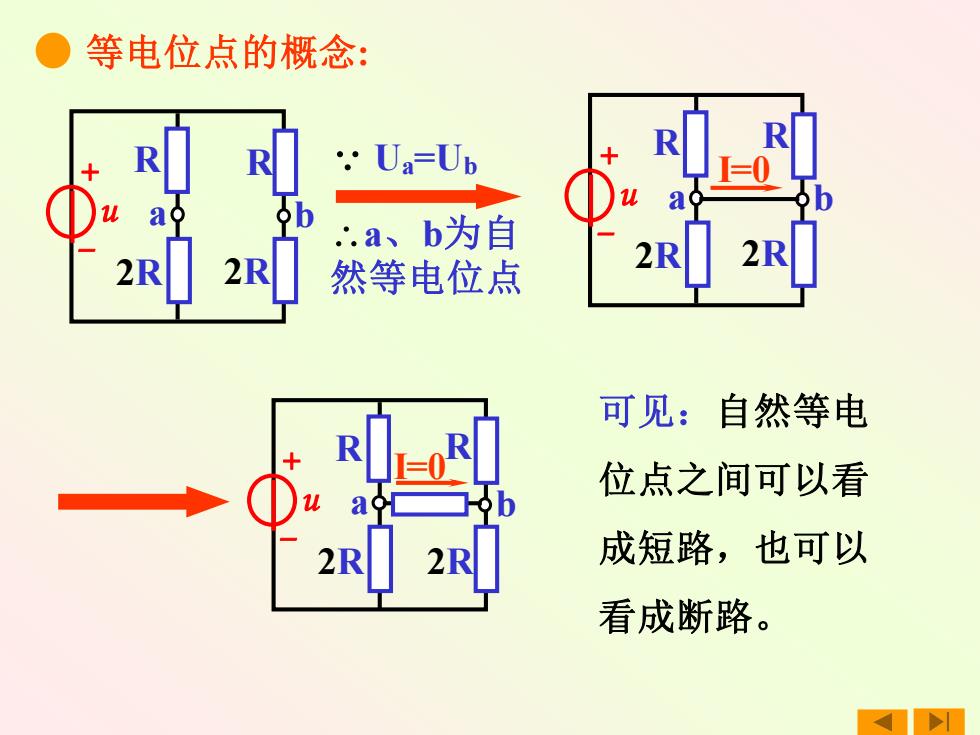
等电位点的概念: u + – R R 2R 2R a b a、b为自 然等电位点 Ua=Ub 可见:自然等电 位点之间可以看 成短路,也可以 看成断路。 u + – R R 2R 2R a b I=0 u + – R R 2R 2R a b I=0

强迫等电位点 2R h UatUp 2R 2R Ua=Ub a、b为强 迫等电位点 利用自然等电位点的概念可以简化电路
强迫等电位点 Ua≠Ub Ua=Ub a、b为强 迫等电位点 利用自然等电位点的概念可以简化电路。 u + – R 2R 2R R a b u + – R 2R 2R R a b I≠0
例1 1122i。0 =? 若以d为参考点, ob 则Ua=Ub=U;a、 10v还I0v还I0v还 b、c为自然等电 位点。 nsas-7 =10A 10v 0.52
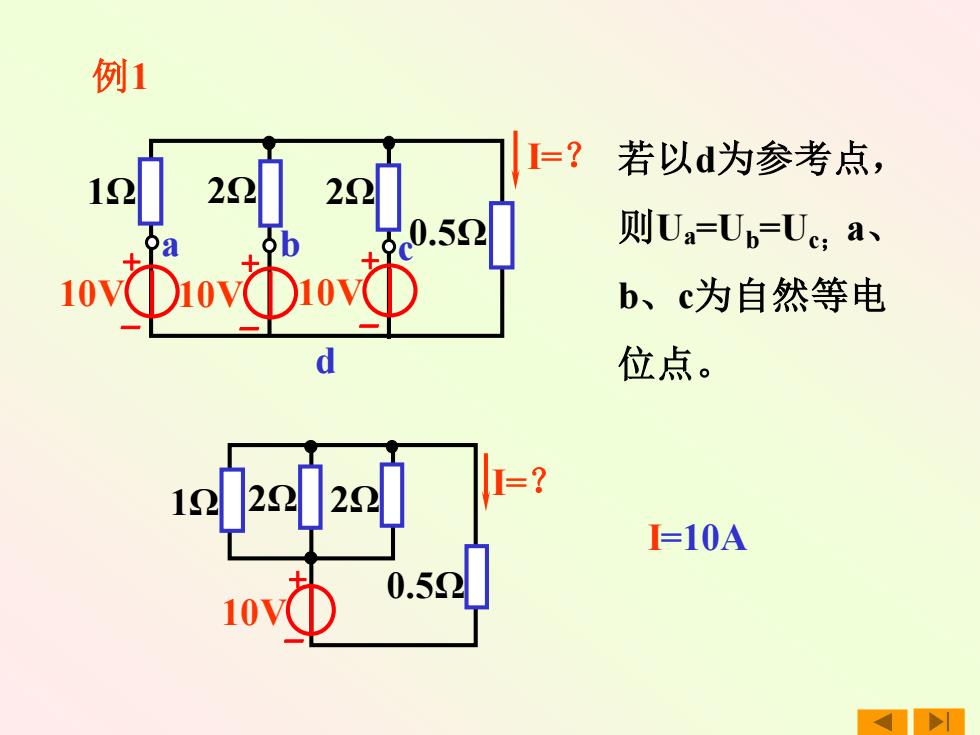
例1 a b c d 若以d为参考点, 则Ua=Ub=Uc;a、 b、c为自然等电 位点。 1Ω + – 10V 2Ω 2Ω 0.5Ω I=? + – 10V + – 10V + – I=? 0.5Ω 1Ω 2Ω 2Ω 10V I=10A