
单位重量流体经叶轮后的静压能增加为: Hp 4,2422w2 ((2-11) 2g 2g 2 2 Hr 4242 w2 2 w,222c2 2 (2-13) 2g 28 2g 根据余弦定理,上述速度之间的关系可表示为: W c242 2cu cosA (2-5,6) 2 W2 2 42 2c242 cosA2
单位重量流体经叶轮后的静压能增加为: g w w g u u HP 2 2 2 2 2 1 2 1 2 2 2 2 2 2 1 2 2 2 2 2 1 2 1 2 2 g c c g w w g u u HT (2-13) 根据余弦定理,上述速度之间的关系可表示为: 1 1 1 2 1 2 1 2 1 w c u 2c u cos 2 2 2 2 2 2 2 2 2 w c u 2c u cos (2-11) (2-5,6)
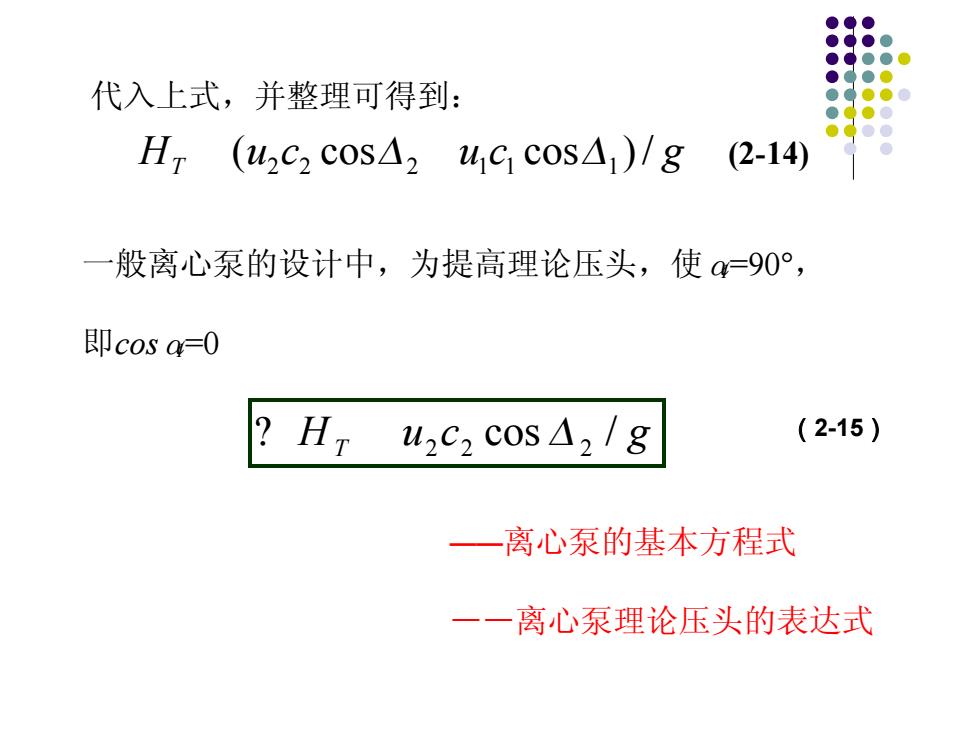
代入上式,并整理可得到: HT (uzc2 cosA2 uc CosA)/g (2-14) 一般离心泵的设计中,为提高理论压头,使=90°, 即cosa4=0 ?Hru2C2cos△2/g (2-15) 一离心泵的基本方程式 一一离心泵理论压头的表达式
代入上式,并整理可得到: HT (u2c2 cos2 u1c1 cos1)/ g (2-14) 一般离心泵的设计中,为提高理论压头,使α1=90° , 即cosα1=0 ——离心泵的基本方程式 ——离心泵理论压头的表达式 HT u2c2 cos 2 / g (2-15)

H u2C2c0S△2/g (2)流量和理论压头的关系 流量可表示为叶轮出口处的径向速度与出口截面积的乘积 qy 22r,b2C2S1n△2 (2-7) 从点2处的速度三角形可以得出 C2 CosA2 uz c2 sinA2 cigE2 代入H=U2C2c0s02g H (4,92sin△,cgE,) 2,b28 9r(2-18) 8 其中:u22r,n/60,n一叶轮转速,r/min 表示离心泵的理论压头与理论流量,叶轮的转速和直径、叶 轮的几何形状间的关系
(2)流量和理论压头的关系 流量可表示为叶轮出口处的径向速度与出口截面积的乘积 2 2 2 2 qV 2r b c sin 从点2处的速度三角形可以得出 2 2 2 2 2 2 c cos u c sin ctg 代入 HT=u2c2cosα2/g T qV r b g u ctg g u u c ctg g u H 2 2 2 2 2 2 2 2 2 2 2 2 ( sin ) 其中:u2 2ðr2n/60,n —叶轮转速,r/min 表示离心泵的理论压头与理论流量,叶轮的转速和直径、叶 轮的几何形状间的关系。 HT u2c2 cos2 / g (2-7) (2-18)

对于某个离心泵(即其B2、r2、b2固定),当转速n定时, 理论压头与理论流量之间呈线形关系,可表示为: H A Bqy H uctgE 2.1.1.3离心泵理论压头影响因素分析 25,b28 22n (1)叶轮的转速和直径 60 当叶片几何尺寸(b2,B2)与理论流量一定时,离心泵的理 论压头随叶轮的转速或直径的增加而加大。 qvcn,那么HTOC n2 (2)叶片的几何形状
对于某个离心泵(即其β2、r2、b2固定),当转速n一定时, 理论压头与理论流量之间呈线形关系,可表示为: HT A BqV 2.1.1.3 离心泵理论压头影响因素分析 (1)叶轮的转速和直径 当叶片几何尺寸(b2,β2)与理论流量一定时,离心泵的理 论压头随叶轮的转速或直径的增加而加大。 (2)叶片的几何形状 根据叶片出口端倾角β2的大小,叶片形状可分为三种: T qV r b g u ctg g u H 2 2 2 2 2 2 2 60 2 2 2 r n u qV∝n,那么HT∝n2
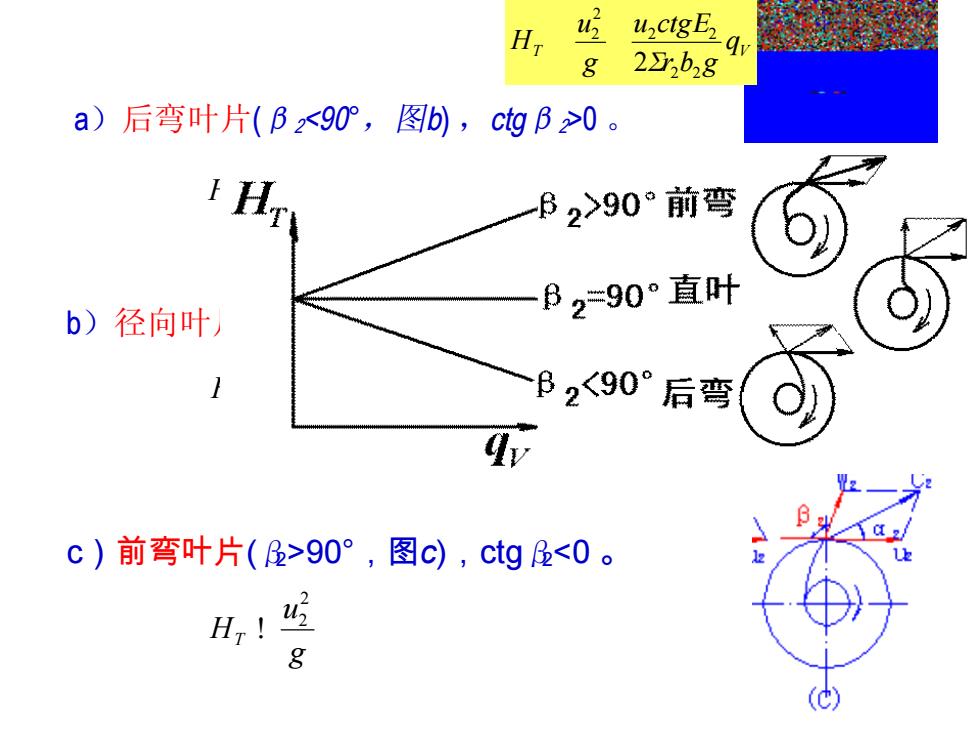
H uctgE 8 235b28 a)后弯叶片(B<90°,图b),ctgB≥0。 H 62>90°前弯 B290°直叶 b)径向叶 1 B2<90°后弯 c)前弯叶片(B>90°,图c),ctgB<0
a)后弯叶片(β2<90°,图b) ,ctgβ2>0 。 b)径向叶片(β2=90°,图a),ctgβ2=0 。 c)前弯叶片(β2>90° ,图c),ctgβ2<0 。 g u HT 2 2 g u HT 2 2 g u HT 2 2 T V q r b g u ctg g u H 2 2 2 2 2 2 2