
连通域:了解复球面,无穷远点,扩充复平面的概念 3.教学重点难点:复数的方根,复数的各种表示法 4教学建议:(1)根据课程的特点,建议教学形式以课堂教学为主。 (2)讲授内容以讲清楚基本理论为目的,由于解题练习是数学课教学的一个重 要环节,建议每次课(2学时)布置一次作业,由学生独立完成。 (3)建议习题课的安排约为每章二课时,可利用课外答疑的方式进行。 第二章:解析函数 1,基本内容 2.1复变函数的概念、极限与连续性 2.2解析函数的概念 2.3函数可导与解析的充要条件 2.4初等函数 2.教学基本要求: 了解复变函数的概念、极限与连续性,理解复变函数的导数概念及解析函数的概念及解析 函数与柯西一黎曼方程的联系,了解某些初等解析函数的基本性质。 3.教学重点难点: 解析函数的判别方法 4.敦学建议: ()根据课程的特点,建议教学形式以课堂教学为主。 (☑)简单讲授复变函数的极限和连续性,重点讲授解析函数的定义和充分必要条件。让 学生了解几类初等函数的定义和性质,为以后它们的Taylor展开做准备。 第三章:复变函数的积分 1.基本内容: 3.1复变函数积分的概念 3.2柯西一古萨基本定理及其推广 3.3柯西积分公式及其推论 3.4解析函数与调和函数的关系 2.教学基本要求: 理解积分的定义,了解其性质,会求积分:掌握柯西定理、复合闭路定理、柯西积分公式 和高阶导数公式:了解调和函数与解析函数的关系,掌握从解析函数的实(虚)部求其虚(实
连通域;了解复球面,无穷远点,扩充复平面的概念. 3.教学重点难点:复数的方根, 复数的各种表示法 4.教学建议:(1)根据课程的特点,建议教学形式以课堂教学为主。 (2)讲授内容以讲清楚基本理论为目的,由于解题练习是数学课教学的一个重 要环节,建议每次课(2 学时)布置一次作业,由学生独立完成。 (3)建议习题课的安排约为每章二课时,可利用课外答疑的方式进行。 第二章:解析函数 1. 基本内容: 2.1 复变函数的概念、极限与连续性 2.2 解析函数的概念 2.3 函数可导与解析的充要条件 2.4 初等函数 2. 教学基本要求: 了解复变函数的概念、极限与连续性,理解复变函数的导数概念及解析函数的概念及解析 函数与柯西—黎曼方程的联系,了解某些初等解析函数的基本性质。 3. 教学重点难点: 解析函数的判别方法 4. 教学建议: (1) 根据课程的特点,建议教学形式以课堂教学为主。 (2) 简单讲授复变函数的极限和连续性,重点讲授解析函数的定义和充分必要条件。让 学生了解几类初等函数的定义和性质,为以后它们的 Taylor 展开做准备。 第三章:复变函数的积分 1. 基本内容: 3.1 复变函数积分的概念 3.2 柯西—古萨基本定理及其推广 3.3 柯西积分公式及其推论 3.4 解析函数与调和函数的关系 2. 教学基本要求: 理解积分的定义,了解其性质,会求积分;掌握柯西定理、复合闭路定理、柯西积分公式 和高阶导数公式;了解调和函数与解析函数的关系,掌握从解析函数的实(虚)部求其虚(实 5

部)的方法。 3.教学重点难点: 柯西定理、复合闭路定理、柯西积分公式和高阶导数公式,从解析函数的实(虚)部求 其虚(实部)的方法 4.教学建议: (1)根据课程的特点,建议教学形式以课堂教学为主。 (2)重点讲授何西积分公式和高阶导数公式适用的条件。举例说明这两个公式的应用。 齐次,对于非闭曲线上解析函数的积分,则考虑复变函数的牛顿莱布尼兹公式。 第四章:解析函数的级数表示 1.基本内容: 4.1复数项级数 4.2复变函数项级数 4.3解析函数的泰勒展开 4.4解析函数的洛朗展开 4.5孤立奇点 2.敦学基本要求: 理解复数项级数、幂级数收敛、发散概念,了解幂级数的基本性质以及收敛半径的求法: 掌握简单函数在不同圆环域内展开为罗朗级数的间接方法。理解孤立奇点及其分类。 3.教学重点难点; 幂级数收敛半径的求法,解析函数的洛朗展开。 4.敷学建议: (1)根据课程的特点,建议教学形式以课堂教学为主。 (2)着重讲授在圆盘内解析的函数的Taylor展开以及在圆环内解析的函数的Laurent展开 的方法。 第五章:留数理论及其应用 1.基本内容 5.1留数 52留数在积分计算中应用 2.教学基本要求: 理解留数的概念及留数定理:熟练掌握极点处留数的求法及用留数求某些定积分的计算方
部)的方法。 3. 教学重点难点: 柯西定理、复合闭路定理、柯西积分公式和高阶导数公式,从解析函数的实(虚)部求 其虚(实部)的方法。 4. 教学建议: (1)根据课程的特点,建议教学形式以课堂教学为主。 (2)重点讲授柯西积分公式和高阶导数公式适用的条件。举例说明这两个公式的应用。 齐次,对于非闭曲线上解析函数的积分,则考虑复变函数的牛顿-莱布尼兹公式。 第四章:解析函数的级数表示 1. 基本内容: 4.1 复数项级数 4.2 复变函数项级数 4.3 解析函数的泰勒展开 4.4 解析函数的洛朗展开 4.5 孤立奇点 2. 教学基本要求: 理解复数项级数、幂级数收敛、发散概念,了解幂级数的基本性质以及收敛半径的求法; 掌握简单函数在不同圆环域内展开为罗朗级数的间接方法。理解孤立奇点及其分类。 3. 教学重点难点: 幂级数收敛半径的求法,解析函数的洛朗展开。 4. 教学建议: (1)根据课程的特点,建议教学形式以课堂教学为主。 (2)着重讲授在圆盘内解析的函数的 Taylor 展开以及在圆环内解析的函数的 Laurent 展开 的方法。 第五章:留数理论及其应用 1. 基本内容: 5.1 留数 5.2 留数在积分计算中应用 2. 教学基本要求: 理解留数的概念及留数定理;熟练掌握极点处留数的求法及用留数求某些定积分的计算方 6

法。 3.教学重点难点: 留数定理,留数求某些定积分的计算方法。 4.教学建议: (1)根据课程的特点,建议教学形式以课堂教学为主。 (2)让学生掌握留数定理应用的广泛性,充分理解留数定理是柯西古萨定理、柯西积分 公式、高阶导数公式的推广,引导学生理解函数在闭曲线上积分为零的本质。 第七章:傅里叶变换 1.基本内容: 71傅里叶变换的概念 7.2单位脉冲函数(6函数) 7.3傅里叶变换的性质 2.教学基本要求: 理解傅氏变换的概念:了解6函数及其性质:掌握傅氏变换性质和卷积定理。 3.教学重点难点: 傅氏变换性质和卷积定理, 4.教学建议: (1)根据课程的特点,建议教学形式以课堂教学为主。 (2)让学生理解傅里叶变换的来源以及与傅里叶级数的区别和联系。掌握特殊函数的傅 里叶变换。 第八章:拉普拉斯变换 1.基本内容 8.1拉普拉斯变换的概色 8.2拉氏变换的性质 8.3拉普拉斯逆变换 8.4拉氏变换的应用 2.教学基本要求: 理解拉氏变换概念:掌握拉氏变换的性质和卷积定理:会求有理函数的拉氏逆变换:掌握 用拉氏变换解微分方程的方法。 3.数学重点难点:
法。 3. 教学重点难点: 留数定理,留数求某些定积分的计算方法。 4. 教学建议: (1)根据课程的特点,建议教学形式以课堂教学为主。 (2)让学生掌握留数定理应用的广泛性,充分理解留数定理是柯西-古萨定理、柯西积分 公式、高阶导数公式的推广,引导学生理解函数在闭曲线上积分为零的本质。 第七章:傅里叶变换 1. 基本内容: 7.1 傅里叶变换的概念 7.2 单位脉冲函数(δ函数) 7.3 傅里叶变换的性质 2. 教学基本要求: 理解傅氏变换的概念;了解δ函数及其性质;掌握傅氏变换性质和卷积定理。 3. 教学重点难点: 傅氏变换性质和卷积定理。 4. 教学建议: (1)根据课程的特点,建议教学形式以课堂教学为主。 (2)让学生理解傅里叶变换的来源以及与傅里叶级数的区别和联系。掌握特殊函数的傅 里叶变换。 第八章:拉普拉斯变换 1. 基本内容: 8.1 拉普拉斯变换的概念 8.2 拉氏变换的性质 8.3 拉普拉斯逆变换 8.4 拉氏变换的应用 2. 教学基本要求: 理解拉氏变换概念;掌握拉氏变换的性质和卷积定理;会求有理函数的拉氏逆变换;掌握 用拉氏变换解微分方程的方法。 3. 教学重点难点: 7
拉氏变换的性质和卷积定理,拉氏变换解微分方程的方法 4.教学建议: (1)根据课程的特点,建议教学形式以课堂教学为主。 (2)重点讲授并带领学生练习拉氏变换的各种性质,为用拉氏变换求解微分方程打下基 础。 四、教学环节与学时分配 课外辅 总学 导 教学内容 备注 号 时 讲课 实验 上机其他 课外实 1复数与复平面 2解析函数 3复变函数的积分 解析函数的级数表示 留数理论及其应用 傅里叶变换 7拉普拉斯变换 1010 五、教学中应注意的问题: 本课程应把重点放在培养学生正确地理解和运用基本概念与基本方法上,并重视理论联系 实际,从学生专业课程出发来讲授此课,做到有的放矢,以提高学生分析问题和解决问题的能 力。 六、实验/实践内容: 无 七、考核方式: 考核方式为考试。严格考核学生出勤情况,达到学籍管理规定的旷课量取消考试资格。综 合成绩根据平时成绩和期末成绩评定,平时成绩30%,期末成绩占70%,考试内容参照考试 大纲。 八、教材及主要参考书: 1、选用教材: 《复变函数与积分变换》(修订版),马柏林等,复旦大学出版社,2007 2、主要参考书: 1)《复变函数与积分变换》,华中科技大学数学系,高等教有出版社,2003 2)《复变函数》,西安交通大学高等数学教研室,高等教有出版社,1994 8
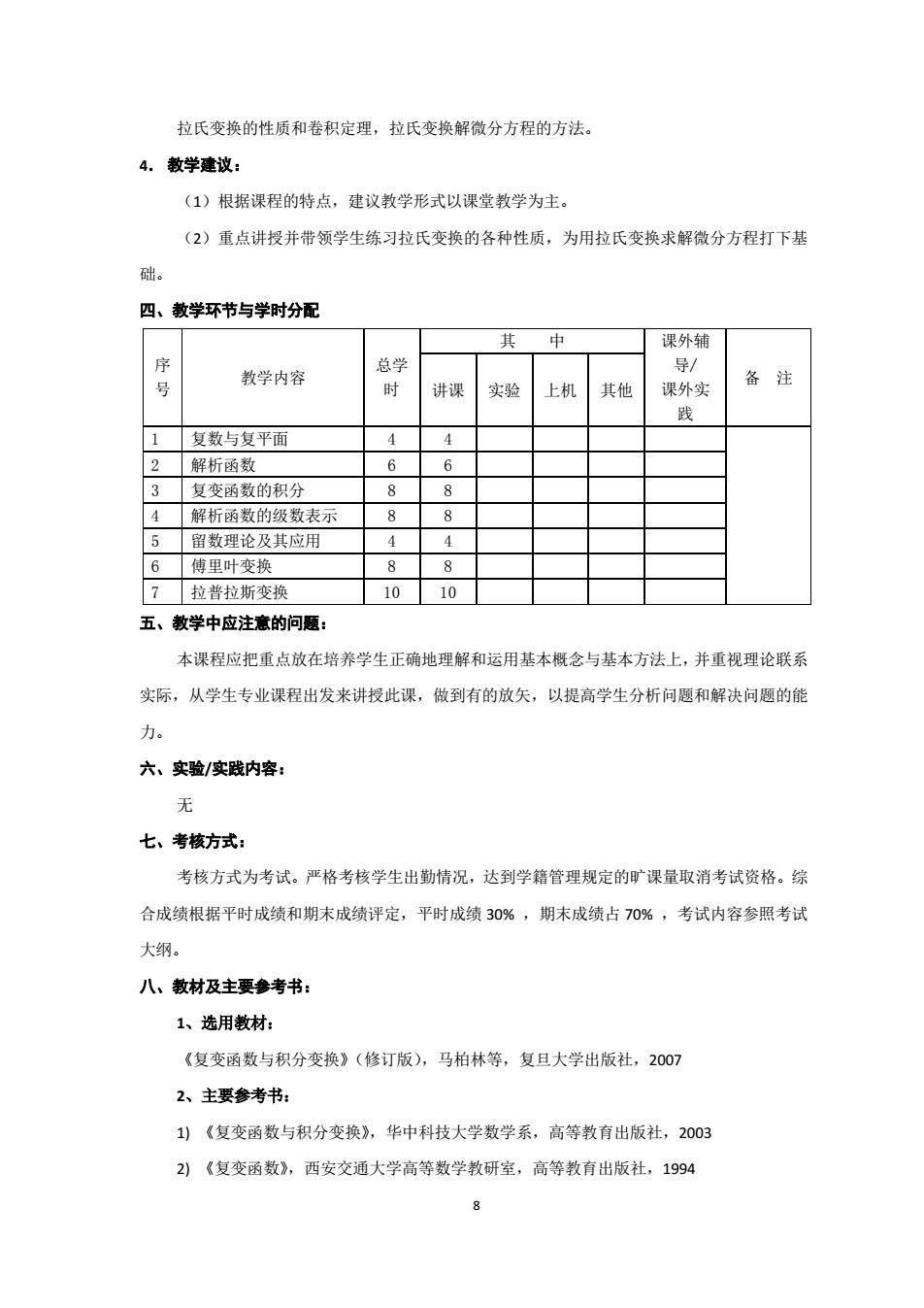
拉氏变换的性质和卷积定理,拉氏变换解微分方程的方法。 4. 教学建议: (1)根据课程的特点,建议教学形式以课堂教学为主。 (2)重点讲授并带领学生练习拉氏变换的各种性质,为用拉氏变换求解微分方程打下基 础。 四、教学环节与学时分配 序 号 教学内容 总学 时 其 中 课外辅 导/ 课外实 践 备 注 讲课 实验 上机 其他 1 复数与复平面 4 4 2 解析函数 6 6 3 复变函数的积分 8 8 4 解析函数的级数表示 8 8 5 留数理论及其应用 4 4 6 傅里叶变换 8 8 7 拉普拉斯变换 10 10 五、教学中应注意的问题: 本课程应把重点放在培养学生正确地理解和运用基本概念与基本方法上,并重视理论联系 实际,从学生专业课程出发来讲授此课,做到有的放矢,以提高学生分析问题和解决问题的能 力。 六、实验/实践内容: 无 七、考核方式: 考核方式为考试。严格考核学生出勤情况,达到学籍管理规定的旷课量取消考试资格。综 合成绩根据平时成绩和期末成绩评定,平时成绩 30% ,期末成绩占 70% ,考试内容参照考试 大纲。 八、教材及主要参考书: 1、选用教材: 《复变函数与积分变换》(修订版),马柏林等,复旦大学出版社,2007 2、主要参考书: 1) 《复变函数与积分变换》,华中科技大学数学系,高等教育出版社,2003 2) 《复变函数》,西安交通大学高等数学教研室,高等教育出版社,1994 8

3)《积分变换》,南京工学院数学教研室,高等教有出版社,1987 4)《复变函数与积分变换学习辅导与习题全解》,高等教有出版,2003 九、教改说明及其他: 因课时偏少,目前各教学课本及参考书并不是很适合本校学生,建议加强教研教改,启用自 编教材。 执笔人:朱晖系室审核人:王恒太
3) 《积分变换》, 南京工学院数学教研室,高等教育出版社,1987 4) 《复变函数与积分变换学习辅导与习题全解》,高等教育出版,2003 九、教改说明及其他: 因课时偏少,目前各教学课本及参考书并不是很适合本校学生,建议加强教研教改,启用自 编教材。 执笔人:朱晖 系室审核人:王恒太 9