
Case Study:快排序算法的并行化 算法5.2中描述了使用2m个处理器完成对n个输入数据 排序的并行算法 procedure para_quicksort(data,i,j,m,id) 算法52快速排序并行算法 Begin 输入:无序数组data[1,n],使用 (1)if (j-i)sk or m=o then 的处理器个数2m (1.1)P_id call quicksort(data,i,j) 输出:有序数组data[1,n] else Begin (1.2)P_id:r=partition(data,i,j) para_quicksort(data,1,n,m,o) (1.3)P_id send data[r+1,j]to P_id+2m-11 End (1.4)para_quicksort(data,i,r-1,m-1,id) (1.5)para_quicksort(data,r+1,j,m-1,id+2m-1-1) (1.6)P id+2T-1 send data[r+1,j]back to P id end if End 13 2011/10/18
Case Study:快排序算法的并行化 13 2011/10/18 算法5.2中描述了使用2个处理器完成对n个输入数据 排序的并行算法. 算法5.2 快速排序并行算法 输入:无序数组data[1,n],使用 的处理器个数2 输出:有序数组data[1,n] Begin para_quicksort(data,1,n,m,0) End procedure para_quicksort(data,i,j,m,id) Begin (1)if (j‐i)≤k or m=0 then (1.1)P_id call quicksort(data,i,j) else (1.2)P_id: r=partition(data,i,j) (1.3)P_id send data[r+1,j] to P_id+2ିଵ‐1 (1.4)para_quicksort(data,i,r‐1,m‐1,id) (1.5)para_quicksort(data,r+1,j,m‐1,id+2ିଵ‐1) (1.6)P_id+2‐1 send data[r+1,j] back to P_id end if End
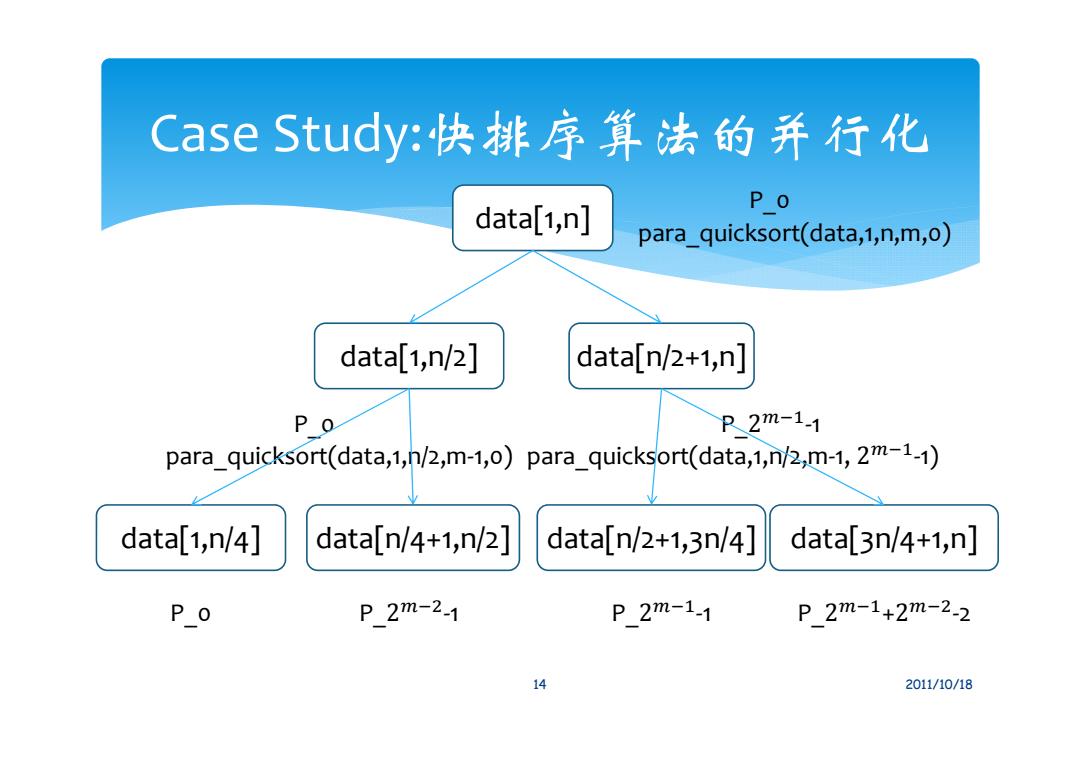
Case Study:快排序算法的并行化 data[1,n] para_quicksort(data,1,n,m,o) data[1,n/2] data[n/2+1,n] PO R2m-1-1 para_quicksort(data,1,h/2,m-1,0)para_quicksort(data,1,n/2,m-1,2m-1-1) data[1,n/4] data[n/4+1,n/2] data[n/2+1,3n/4] data[3n/4+1,n] P_o P_2m-2-1 P_2m-1-1 P2m-1+2m-2-2 14 2011/10/18
Case Study:快排序算法的并行化 14 2011/10/18 data[1,n] data[1,n/2] data[n/2+1,n] para_quicksort(data,1,n,m,0) P_0 para_quicksort(data,1,n/2,m‐1,0) P_0 para_quicksort(data,1,n/2,m‐1, 2ିଵ‐1) P_2ିଵ‐1 data[1,n/4] data[n/4+1,n/2] data[n/2+1,3n/4] data[3n/4+1,n] P_0 P_2ିଶ‐1 P_2ିଵ‐1 P_2ିଵ+2ିଶ‐2

Case Study::快排序算法的并行化 *快速排序算法5.2的性能 *由于左右分支可以并行处理,所以总体执行时间 T(n)=T(n/2)+n。 米 根据Master定理,所以算法5.2的时间复杂度为 o(n)。 *算法52是一种很自然的并行化方法,通过并行的 调用快排序对两个所划分的子序列进行快排序。 但是这种并行化的方法并未改变串行算法本身的 属性,但是划分时间就是O()。要进一步提高效 率,只有将划分步进行并行化才有可能得到成本 最优的算法。 15 2011/10/18
15 2011/10/18 Case Study:快排序算法的并行化 快速排序算法5.2的性能 由于左右分支可以并行处理,所以总体执行时间 T(n)=T(n/2)+n。 根据Master定理,所以算法5.2的时间复杂度为 Θ(n)。 算法5.2是一种很自然的并行化方法,通过并行的 调用快排序对两个所划分的子序列进行快排序。 但是这种并行化的方法并未改变串行算法本身的 属性,但是划分时间就是O(n)。要进一步提高效 率,只有将划分步进行并行化才有可能得到成本 最优的算法

Case Study:快排序算法的并行化 *Master定理 Theorem A.3.68.Master Theorem Let a,b,and c be positive integers.Let T(1)=0, T(n)-a.T(2) +b.n. Then, if a<c, Tm)={ O(nloge n)ifc<a. 16 2011/10/18
16 2011/10/18 Case Study:快排序算法的并行化 Master定理

Case Study:快排序算法的并行化 算法5.3PRAM-CRCN上为快排序构造二又树算法 *输入:序列(A1.,An)和n个处理器 *输出:供快速排序用的一棵二叉树 Begin (1)For each processor i do (2.3)RCfi=i (1.1)root=I (2.4)if i=RCfi then exit else fi=RCfi endif (1.2)fi=root Endif (1.3)LCi=RCi=n+1 Endrepeat End End (2)Repeat for each processor iroot do If (Ai<Afi)or(Ai=Afi and i<fi)then (2.1)LCfi=i (2.2)if i=LCfi then exit else fi=LCfi endif else 17 2011/10/18
算法5.3 PRAM‐CRCW上为快排序构造二叉树算法 输入:序列(A1,…,An)和n个处理器 输出:供快速排序用的一棵二叉树 Case Study:快排序算法的并行化 17 2011/10/18 Begin (1) For each processor i do (1.1) root=I (1.2) fi=root (1.3) LCi=RCi=n+1 End (2) Repeat for each processor i്root do If (Ai<Afi) or (Ai=Afi and i<fi) then (2.1) LCfi=i (2.2) if i=LCfi then exit else fi=LCfi endif else (2.3) RCfi=i (2.4) if i=RCfi then exit else fi=RCfi endif Endif Endrepeat End