
Example 2 We use the given uniform PDF of X,which is a=80 if30≤x≤60, otherwise. and the corresponding CDF,which is 0 ifx≤30, 5xw={Cx-30/30, if30≤x≤60, 1 if60≤x
Example 2 We use the given uniform PDF of 𝑋, which is 𝑓𝑋 𝑥 = 1/30 if 30 ≤ 𝑥 ≤ 60, 0 otherwise. and the corresponding CDF, which is 𝐹𝑋 𝑥 = 0 if 𝑥 ≤ 30, (𝑥 − 30)/30, if 30 ≤ 𝑥 ≤ 60, 1 if 60 ≤ 𝑥

Example 2 Thus, =0s1-5() 0 ifx 180 ≤ 60 180 30 二 了1- y 180 180 f ≤ 30 y ≤ 60 30) f 180 1 ≤ 30 y
Example 2 Thus, 𝐹𝑌 𝑦 = 𝑃 180 𝑦 ≤ 𝑋 = 1 − 𝐹𝑋 180 𝑦 = 0 if 𝑥 ≤ 180 60 , 1 − 180 𝑦 −30 30 if 180 60 ≤ 𝑦 ≤ 180 30 , 1 if 180 30 ≤ 𝑦

Example 2 0 ify≤3, ={2-(6/y) if3≤y≤6, if6≤y. Differentiating this expression,we obtain the PDF of Y: ify≤3, if3≤y≤6, if6≤y
Example 2 = 0 if 𝑦 ≤ 3, 2 − (6/𝑦) if 3 ≤ 𝑦 ≤ 6, 1 if 6 ≤ 𝑦. Differentiating this expression, we obtain the PDF of 𝑌: 𝑓𝑌 𝑦 = 0 if 𝑦 ≤ 3, 6/𝑦 2 if 3 ≤ 𝑦 ≤ 6, 0 if 6 ≤ 𝑦
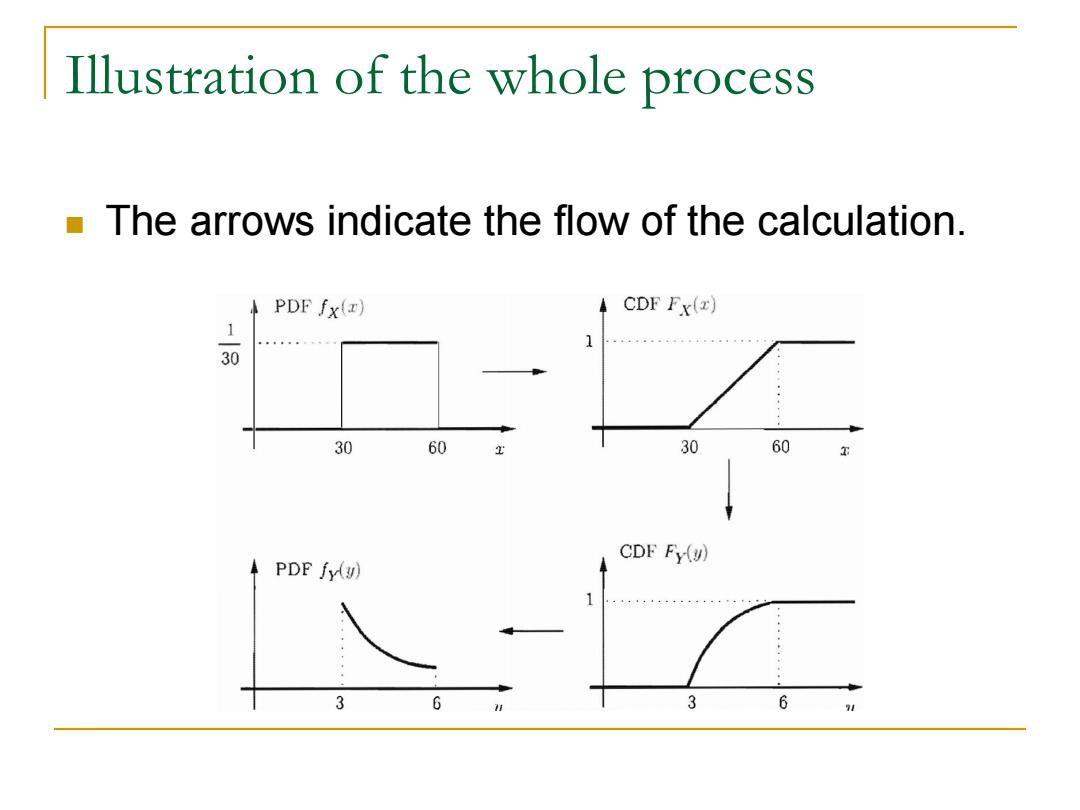
Illustration of the whole process The arrows indicate the flow of the calculation. PDF fx() CDF Fx(z) 1 30 60 30 60 CDF Fy(y) PDF fy(u) 3 3 6
Illustration of the whole process The arrows indicate the flow of the calculation

Example 3 Let Y=g()=X2,where X is a random variable with known PDF. ■For any y≥0,we have Fy(y)=P(Y≤y) =P(X2≤y) =P(-≤X≤V) Fx(y)-Fx()
Example 3 Let 𝑌 = 𝑔(𝑋) = 𝑋 2 , where 𝑋 is a random variable with known PDF. For any 𝑦 ≥ 0 , we have 𝐹𝑌 𝑦 = 𝑃 𝑌 ≤ 𝑦 = 𝑃 𝑋 2 ≤ 𝑦 = 𝑃 − 𝑦 ≤ 𝑋 ≤ 𝑦 = 𝐹𝑋 𝑦 − 𝐹𝑋 − 𝑦