
§4.2欧姆定律与焦耳定律 一、 欧姆定律 二、 焦耳定律 三、 经典电子论观点解释 四、 欧姆定律的失效问题
§4.2 欧姆定律与焦耳定律 一 、欧姆定律 二、焦耳定律 三、经典电子论观点解释 四、欧姆定律的失效问题

现在我们来分析导体中电流和电场的关系。 一、 欧姆定律 中学已知,由实验得在直流电路中导线内, 欧姆定律 为: U I= 或 U=IR. (4.2.1) R 电阻的倒数叫做电导,用G表示:G= (4.2.2) 单位是(欧姆-),称为西门 R 子],符号为S。 R= (4.2.3) ■电阻率的倒数称为电导率, 用0表示: (4.2.4) 电导率的单位为(欧米)l,或S·m-可
一 、欧姆定律 中学已知,由实验得在直流电路中导线内,欧姆定律 为: 现在我们来分析导体中电流和电场的关系。 , U I U IR R 或 (4.2.1) ■电阻的倒数叫做电导,用G表示: 单位是([欧姆]1),称为[西门 子],符号为S。 , l R S 1 G . R (4.2.2) (4.2.3) ■电阻率的倒数称为电导率, 用σ表示: 1 . (4.2.4) 电导率的单位为(欧·米)1,或S· m1
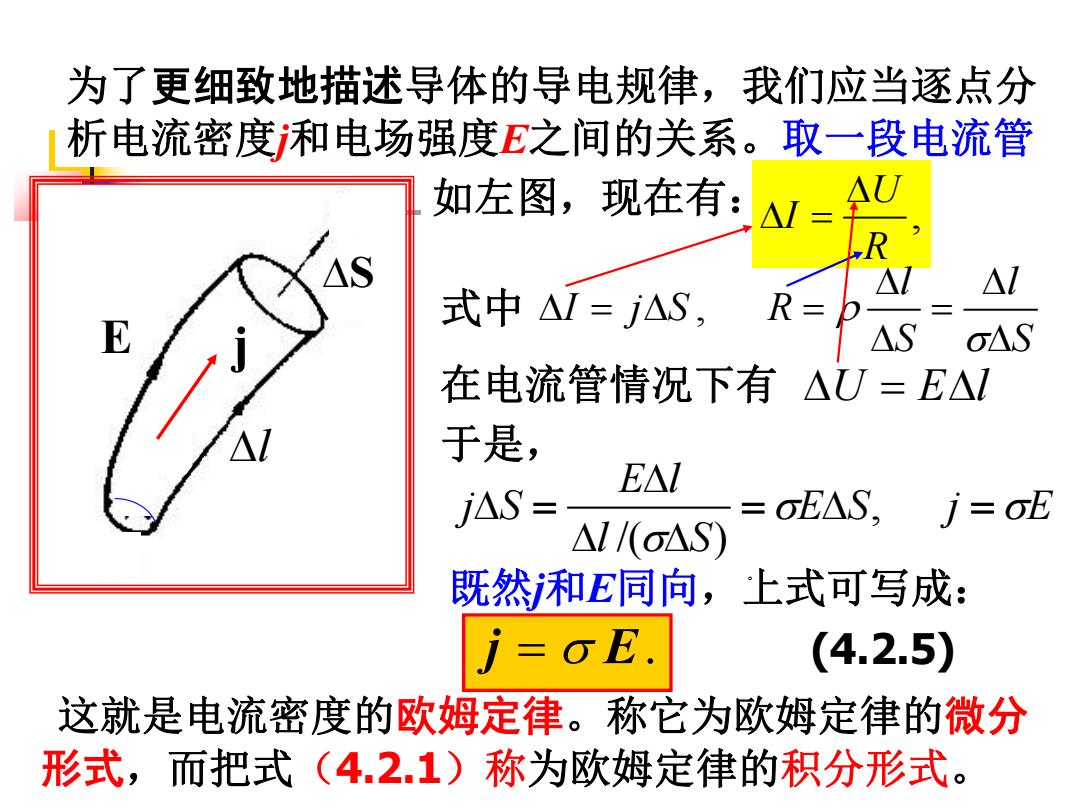
为了更细致地描述导体的导电规律,我们应当逐点分 析电流密度和电场强度E之间的关系。取一段电流管 如左图,现在有: △= AU LR △ △ 式中△1=j△S, R= △S oA.S 在电流管情况下有△J= E△☑ 于是, E△I j△S oE△S, j=oE △l/(o△S) 既然和E同向,上式可写成: j=oE. (4.2.5) 这就是电流密度的欧姆定律。称它为欧姆定律的微分 形式,而把式(4.2.1)称为欧姆定律的积分形式
为了更细致地描述导体的导电规律,我们应当逐点分 析电流密度j和电场强度E之间的关系。取一段电流管 S j l E 如左图,现在有: , U I R , l l I j S R S S 式中 在电流管情况下有 U El 。 于是, E S j E l S E l j S , /( ) 既然j和E同向,上式可写成: j E. (4.2.5) 这就是电流密度的欧姆定律。称它为欧姆定律的微分 形式,而把式(4.2.1)称为欧姆定律的积分形式

■说明:欧姆定律的微分形式更为细致地描述了导体 的导电规律。 (1)从它出发便于说明金属导电的微观机制; (2)便于用场的观点阐述稳恒电路的基本原理; (3)也便于研究大块导体中电流和电场的分布规律; (4)欧姆定律的微分形式比积分形式适用范围更广。 例如对非稳恒情况,实验证明,欧姆定律的微分形式仍 在一定范围内适用于这类非稳恒情况
■ 说明:欧姆定律的微分形式更为细致地描述了导体 的导电规律。 (1)从它出发便于说明金属导电的微观机制; (2)便于用场的观点阐述稳恒电路的基本原理; (3)也便于研究大块导体中电流和电场的分布规律; (4)欧姆定律的微分形式比积分形式适用范围更广。 例如对非稳恒情况,实验证明,欧姆定律的微分形式仍 在一定范围内适用于这类非稳恒情况

二、焦耳定律 中学已学焦耳定律为: =RI2 R 引入单位体积的热功率称为热功率密度,用表示,V 为体积,有:p=P/W=I2R/V。 类似推导欧姆定律的微分形式(4.2.5)的做法,考虑 一段长△1、截面积△的电流管,由 W I=jAS, R=- V=△S 将这三个量代入p中,得: 上式即焦耳定律的微分形式
二、焦耳定律 中学已学焦耳定律为: 2 2 . e U P IU RI R 引入单位体积的热功率称为热功率密度,用p表示,V 为体积,有: p = P/V 。 类似推导欧姆定律的微分形式(4.2.5)的做法,考虑 一段长 、截面积 的电流管,由 I R / V 2 l S , , , l I j S R V S l S 将这三个量代入p 中,得: 2 . j p 上式即焦耳定律的微分形式