
三、 电流连续方程 电流连续方程是电荷守恒定律的数学表示。 按照电荷守恒定律:在孤立系统内,电荷的代数和 保持不变,电荷只能由一个物体转移到另一个物体, 或由物体的某一部分转移到其它部分。 ■ 换言之,如果在导体内任取一闭合曲面S,所围区域 为V,按照电荷守恒定律,则某段时间内流出该曲面S 的电量应当等于同一段时间内区域中电量的减少。这 便可以用数学表达出来: 若在S面上规定面积元矢量S指向外法线方向,则单位 时间内由S面流出的电量应为:{ j.ds
三、 电流连续方程 ■ 电流连续方程是电荷守恒定律的数学表示。 ■ 按照电荷守恒定律:在孤立系统内,电荷的代数和 保持不变,电荷只能由一个物体转移到另一个物体, 或由物体的某一部分转移到其它部分。 ■ 换言之,如果在导体内任取一闭合曲面S,所围区域 为V,按照电荷守恒定律,则某段时间内流出该曲面S 的电量应当等于同一段时间内区域V中电量的减少。这 便可以用数学表达出来: 若在S面上规定面积元矢量dS指向外法线方向,则单位 时间内由S面流出的电量应为: S j dS

与此同时,单位时间内中电量的减少为: ==叮器, dt 根据电荷守恒定律,应有: dt Ot S 即称为电流连续方程的积分形式。 用数学离会,立可符训V…r-小各 鉴于的任意性,于是可得 电流连续方程的微分形式: N●j+t
与此同时,单位时间内V中电量的减少为: , e e V V dq d dV dV dt dt t n 根据电荷守恒定律,应有: 即称为电流连续方程的积分形式。 用数学高斯公式,立即得: ( ) , e V V dV dV t j 鉴于V的任意性,于是可得 电流连续方程的微分形式: j 0. e t . e S V dq d dV dt t j S

说明: ds- q t (1)由于电荷守恒定律的普遍性,上述电流连续方程 也是普遍成立的,与载流导体的物理性质无关; (2)类比静电场的高斯定理,可借助电流线作如下形 象解释。电流线只能起、止于电荷随时间变化的地方。 在电流线的起点附近的区域中,由dg/t<O,会出现 负电荷的不断累积,即电荷密度不断减小; 而在电流线的终点附近的区域中则有dg/dt>O 会出 现正电荷的不断累积,即电荷密度不断增加; 对于电荷密度不随时间变化的地方,电流线既无起点 又无终点,即电流线不可能中断
说明: (1)由于电荷守恒定律的普遍性,上述电流连续方程 也是普遍成立的,与载流导体的物理性质无关; (2)类比静电场的高斯定理,可借助电流线作如下形 象解释。电流线只能起、止于电荷随时间变化的地方。 在电流线的起点附近的区域中,由 ,会出现 负电荷的不断累积,即电荷密度不断减小; 而在电流线的终点附近的区域中则有 ,会出 现正电荷的不断累积,即电荷密度不断增加; 对于电荷密度不随时间变化的地方,电流线既无起点 又无终点,即电流线不可能中断。 dq/ dt 0 dq/ dt 0 dt dq d S j S

稳恒条件 从电流连续方程出发,立刻可导出稳恒电流应满足 的条件。对稳恒电流来说,导体内各点电流密度应与时 间无关,要求dg/dt与时间无关且为零,如果不为零,则 电荷不断积累,电场随时间变化,将破坏电流的稳定 所以: 于是: fis=0,或7j=0 称做稳恒条件的积分形式和微分形式。稳恒条件表明, 电荷分布将不会因稳恒电流的存在而随时间变化,所以 由它产生的电场必然是静电场 ■说明:借助于电流线和电流管的概念,可以对稳恒条 件作如下形象描述:(1)电流线不可能有起点和终点, 即稳恒电流的电流线或电流管一定是闭合的;(2)沿 任一电流管各载面的电流强度都相等
四、 稳恒条件 从电流连续方程出发,立刻可导出稳恒电流应满足 的条件。对稳恒电流来说,导体内各点电流密度应与时 间无关,要求dq/dt与时间无关且为零,如果不为零,则 电荷不断积累,电场随时间变化,将破坏电流的稳定, 所以: , e 0 ,于是: t 0, 0. S d 0 j S 或 j dq dt 称做稳恒条件的积分形式和微分形式。稳恒条件表明, 电荷分布将不会因稳恒电流的存在而随时间变化,所以 由它产生的电场必然是静电场。 ■说明:借助于电流线和电流管的概念,可以对稳恒条 件作如下形象描述:(1)电流线不可能有起点和终点, 即稳恒电流的电流线或电流管一定是闭合的;(2)沿 任一电流管各截面的电流强度都相等
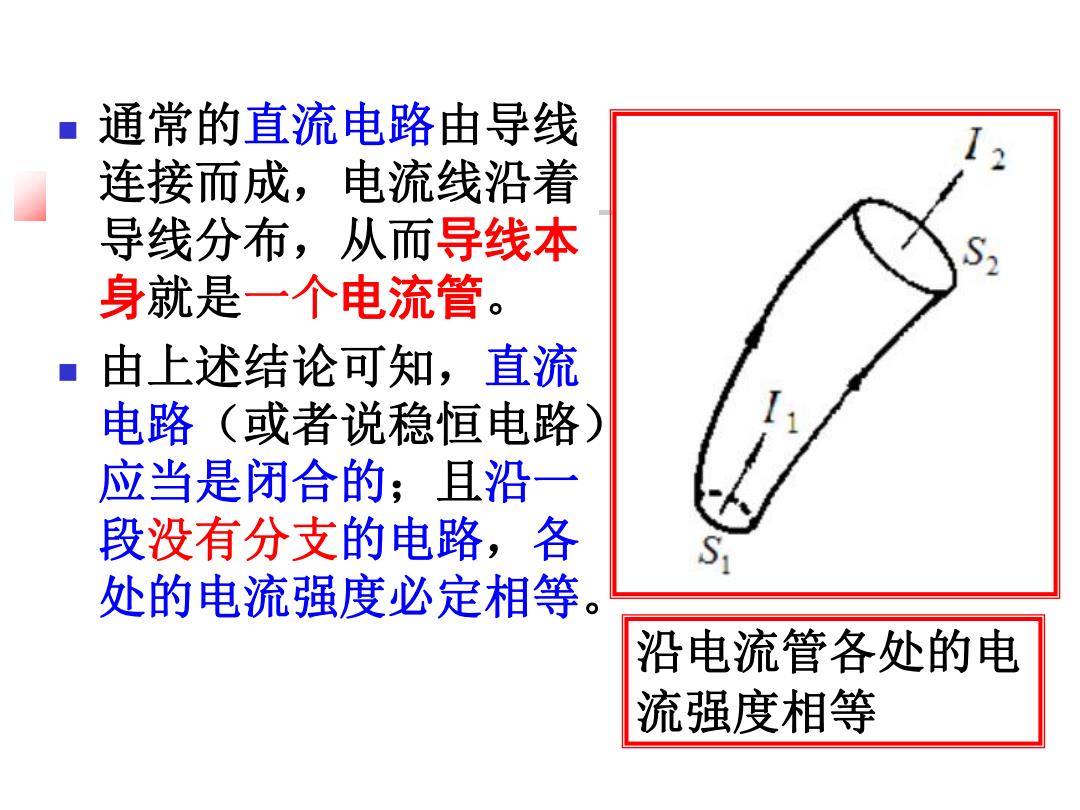
通常的直流电路由导线 连接而成,电流线沿着 导线分布,从而导线本 身就是一个电流管。 由上述结论可知,直流 电路(或者说稳恒电路) 应当是闭合的;且沿一 段没有分支的电路,各 处的电流强度必定相等 沿电流管各处的电 流强度相等
n 通常的直流电路由导线 连接而成,电流线沿着 导线分布,从而导线本 身就是一个电流管。 n 由上述结论可知,直流 电路(或者说稳恒电路) 应当是闭合的;且沿一 段没有分支的电路,各 处的电流强度必定相等。 沿电流管各处的电 流强度相等