
由于这些分支都是由度为1和2的结点射出的,所有 有: B=n1+2*n2 N=B+1=n1+2×n2+1 (6-2) 由式(6-1)和(6-2)得到: n0+n1+n2=n1+2*n2+1 n0=n2+1 下面介绍两种特殊形态的二叉树:满二叉树和完全 二叉树。 一棵深度为k且有2k1个结点的二叉树称为满二叉 树。下图6.9就是一棵满二叉树,对结点进行了顺 序编号
由于这些分支都是由度为1和2的结点射出的,所有 有: B=n1+2*n2 N=B+1=n1+2×n2+1 (6-2) 由式(6-1)和(6-2)得到: n0+n1+n2=n1+2*n2+1 n0=n2+1 下面介绍两种特殊形态的二叉树:满二叉树和完全 二叉树。 一棵深度为k且有2 k -1个结点的二叉树称为满二叉 树。下图6.9就是一棵满二叉树,对结点进行了顺 序编号
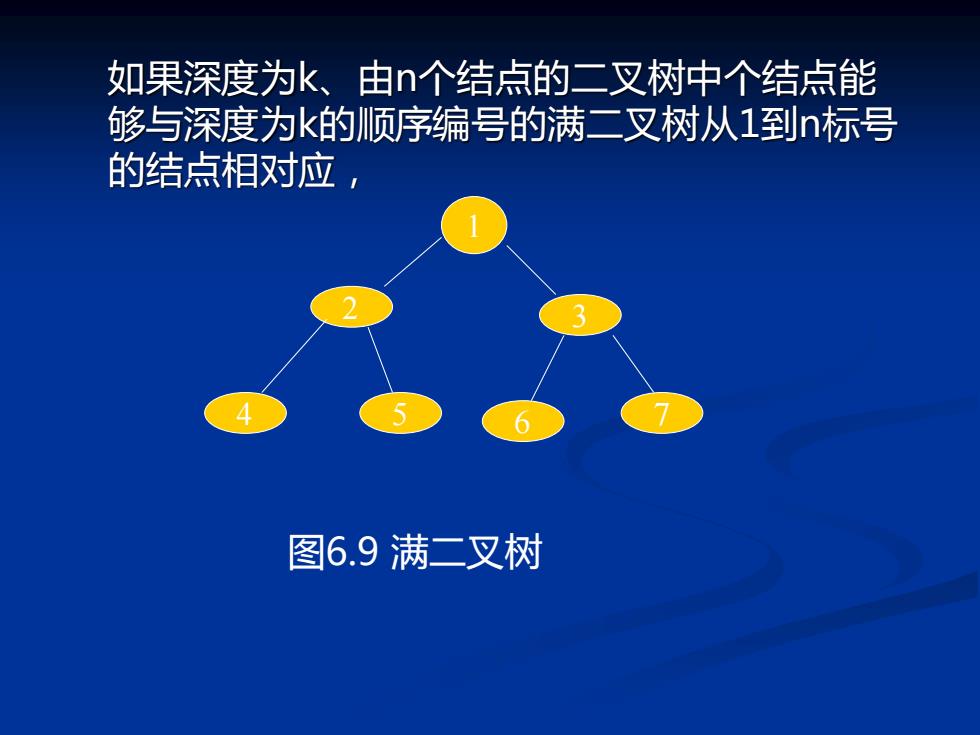
如果深度为k、由个结点的二叉树中个结点能 够与深度为k的顺序编号的满二叉树从I到n标号 的结点相对应 图6.9满二叉树
如果深度为k、由n个结点的二叉树中个结点能 够与深度为k的顺序编号的满二叉树从1到n标号 的结点相对应, 2 4 5 3 6 7 1 图6.9 满二叉树
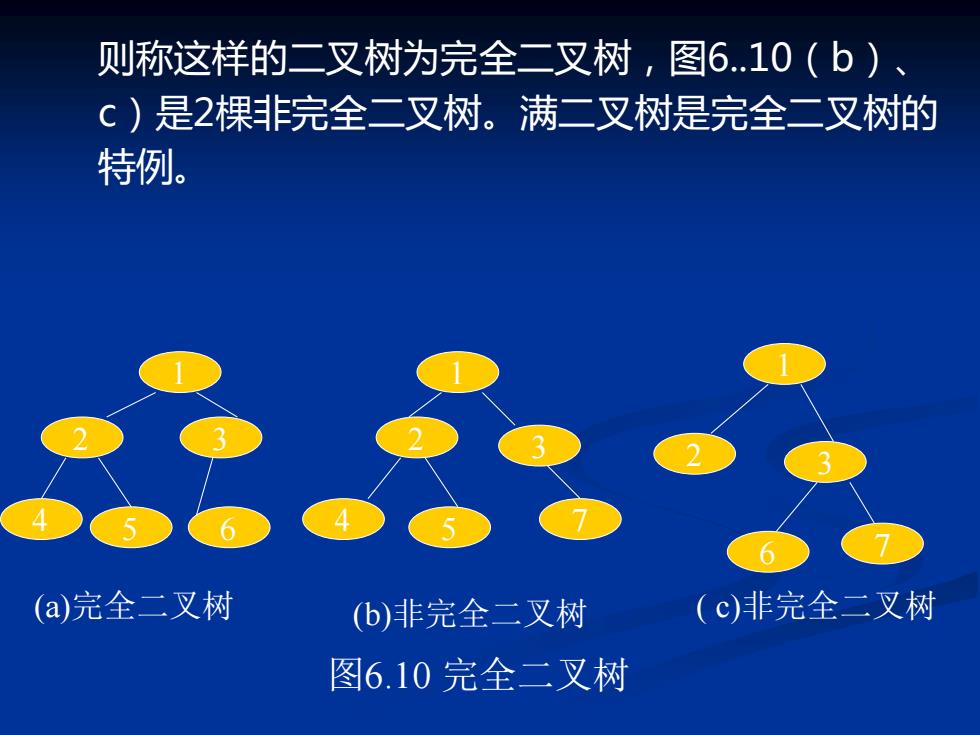
则称这样的二叉树为完全二叉树,图6.10(b)、 c)是2棵非完全二叉树。满二叉树是完全二叉树的 特例。 (a完全二叉树 (b)非完全二叉树 (c)非完全二叉树 图6.10完全二叉树
1 2 3 4 5 6 1 2 3 4 5 7 1 2 3 6 7 (a)完全二叉树 (b)非完全二叉树 ( c)非完全二叉树 图6.10 完全二叉树 则称这样的二叉树为完全二叉树,图6.10(b)、 c)是2棵非完全二叉树。满二叉树是完全二叉树的 特例

完全二叉树的特点是: (1)所有的叶结点都出现在第k层或k-1层。 (2)任一结点,如果其右子树的最大层次为1, 则其左子树的最大层次为1或划+1。 性质4:具有n个结点的完全二叉树的深度为 og2n】+1。符号【x】表示不大于的最大整 数。 假设此二叉树的深度为k,则根据性质2及完全 二叉树的定义得到:2k1-1<n<=2k-1或 2k-1<=n<2k 取对数得到:k-1<=og2n<k因为k是整数。所 以有:k=【log2n】+1
完全二叉树的特点是: (1)所有的叶结点都出现在第k层或k-1层。 (2)任一结点,如果其右子树的最大层次为1, 则其左子树的最大层次为1或l+1。 性质4:具有n个结点的完全二叉树的深度为 【log2n】+1。符号【x】表示不大于x的最大整 数。 假设此二叉树的深度为k,则根据性质2及完全 二叉树的定义得到:2 k-1-1<n<=2k -1 或 2 k-1<=n<2k 取对数得到:k-1<=log2n<k 因为k是整数。所 以有:k=【log2n】+1

性质5:如果对一棵有个结点的完全二叉树的结点按 层序编号(从第1层到第【Iog2n】+1层,每层从左到 右),则对任一结点i(1<=i<=n),有: (1)如果=1,则结点无双亲,是二叉树的根;如 果>1,则其双亲是结点【i/2】。 (2)如果2i>n,则结点为叶子结点,无左孩子;否 则,其左孩子是结点2。 (3)如果2i+1>n,则结点无右孩子;否则,其右 孩子是结点2i+1
性质5: 如果对一棵有n个结点的完全二叉树的结点按 层序编号(从第1层到第【log2n】+1层,每层从左到 右),则对任一结点i(1<=i<=n),有: (1)如果i=1,则结点i无双亲,是二叉树的根;如 果i>1,则其双亲是结点【i/2】。 (2)如果2i>n,则结点i为叶子结点,无左孩子;否 则,其左孩子是结点2i。 (3)如果2i+1>n,则结点i无右孩子;否则,其右 孩子是结点2i+1