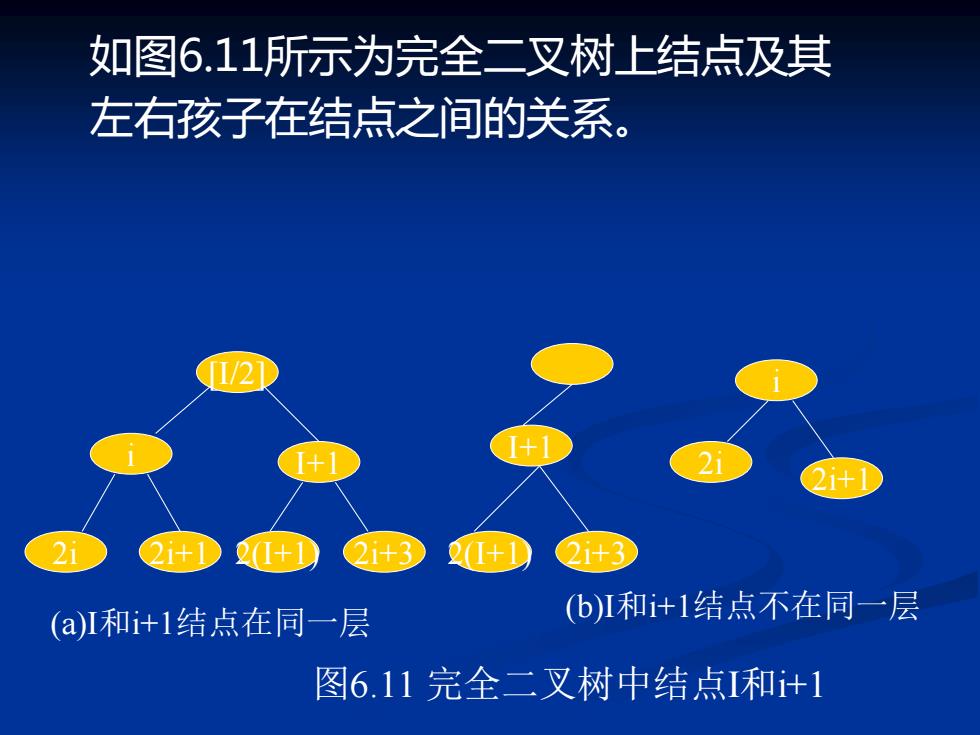
如图6.11所示为完全二叉树上结点及其 左右孩子在结点之间的关系。 I/2 +1 21+1 1+ 2i+3 (a)I和i+1结点在同一层 (b)I和+1结点不在同一层 图6.11完全二叉树中结点I和t1
[I/2] i I+1 2i 2i+1 2(I+1) 2i+3 I+1 2(I+1) 2i+3 i 2i 2i+1 图6.11 完全二叉树中结点I和i+1 (a)I和i+1结点在同一层 (b)I和i+1结点不在同一层 如图6.11所示为完全二叉树上结点及其 左右孩子在结点之间的关系

在此过程中,可以从(2)和(3)推出(1),所 以先证明(2)和(3)。 对于引=1,由完全二叉树的定义,其左孩子是结点2 若2>n,即不存在结点2,此时,结点无左孩子。结 点的由孩子也只能是结点3,若结点3不存在,即3>n 此时结点无右孩子。 对于>1,可分为两种情况: (1)设第(1<=j<=【log2n】)层的第一个结点的 编号为i,由二叉树的性质2和定义知1=21 结点的左孩子必定为j+1层的第一个结点,其编号为 2j=2×21=2i。如果2>n,则无左孩子:
在此过程中,可以从(2)和(3)推出(1),所 以先证明(2)和(3)。 对于i=1,由完全二叉树的定义,其左孩子是结点2, 若2>n,即不存在结点2,此时,结点i无左孩子。结 点i的由孩子也只能是结点3,若结点3不存在,即3>n, 此时结点i无右孩子。 对于i>1,可分为两种情况: (1)设第j(1<=j<=【log2n】)层的第一个结点的 编号为i,由二叉树的性质2和定义知i=2 j-1 结点i的左孩子必定为j+1层的第一个结点,其编号为 2 j=2×2 j-1=2i。如果2 i>n,则无左孩子:

其右孩子必定为第j+1层的第二个结点,编号为2ⅰ+1。 若2i+1>n,则无右孩子。 (2)假设第(1<=j<=【Iog2n】)层上的某个结点 编号为i(20-1)<=i<=2j-1),且2i+1<n,其左孩子为2i 右孩子为2ⅰ+1,则编号为i+1的结点是编号为i的结点 的右兄弟或堂兄弟。若它有左孩子,则其编号必定为 2i+2=2×(i+1):若它有右孩子,则其编号必定为 2i+3=2×(i+1)+1。 当i=1时,就是根,因此无双亲,当i>1时,如果为 左孩子,即2×(i/2)=i,则i/2是i的双亲;如果为右孩 子,i=2p+1,i的双亲应为p,p=(i-1)/2=【i/2】 证毕
其右孩子必定为第j+1层的第二个结点,编号为2i+1。 若2i+1>n,则无右孩子。 (2)假设第j(1<=j<=【log2n】)层上的某个结点 编号为i(2 (j-1)<=i<=2j-1),且2i+1<n,其左孩子为2i, 右孩子为2i+1,则编号为i+1的结点是编号为i的结点 的右兄弟或堂兄弟。若它有左孩子,则其编号必定为 2i+2=2×(i+1):若它有右孩子,则其编号必定为 2i+3=2×(i+1)+1。 当i=1时,就是根,因此无双亲,当i>1时,如果i为 左孩子,即2×(i/2)=i,则i/2是i的双亲;如果i为右孩 子,i=2p+1,i的双亲应为p,p=(i-1)/2=【i/2】. 证毕

6.2.3二叉树的存储结构 1.顺序存储结构 它是用一组连续的存储单元存储二叉树的数 据元素。因此,必须把二叉树的所有结点安排成 为一个恰当的序列,结点在这个序列中的相互位 置能反映出结点之间的逻辑关系,用编号的方法: #define MAX-TREE-SIZE 100 typedef TElemType SqBiTree[MAX-TREE-SIZE]; SqBiTree bt; 从树根起,自上层至下层,每层自左至右的给 所有结点编号缺点是有可能对存储空间造成极大 的浪费,在最坏的情况下,一个深度为且只有 h个结点的右单支树确需要2h-1个结点存储空间。 而且,若经常需要插入与删除树中结点时,顺序 存储方式不是很好!
6.2.3 二叉树的存储结构 1.顺序存储结构 它是用一组连续的存储单元存储二叉树的数 据元素。因此,必须把二叉树的所有结点安排成 为一个恰当的序列,结点在这个序列中的相互位 置能反映出结点之间的逻辑关系,用编号的方法: #define MAX-TREE-SIZE 100 typedef TElemType SqBiTree[MAX-TREE-SIZE]; SqBiTree bt; 从树根起,自上层至下层,每层自左至右的给 所有结点编号缺点是有可能对存储空间造成极大 的浪费,在最坏的情况下,一个深度为h且只有 h个结点的右单支树确需要2 h-1个结点存储空间。 而且,若经常需要插入与删除树中结点时,顺序 存储方式不是很好!
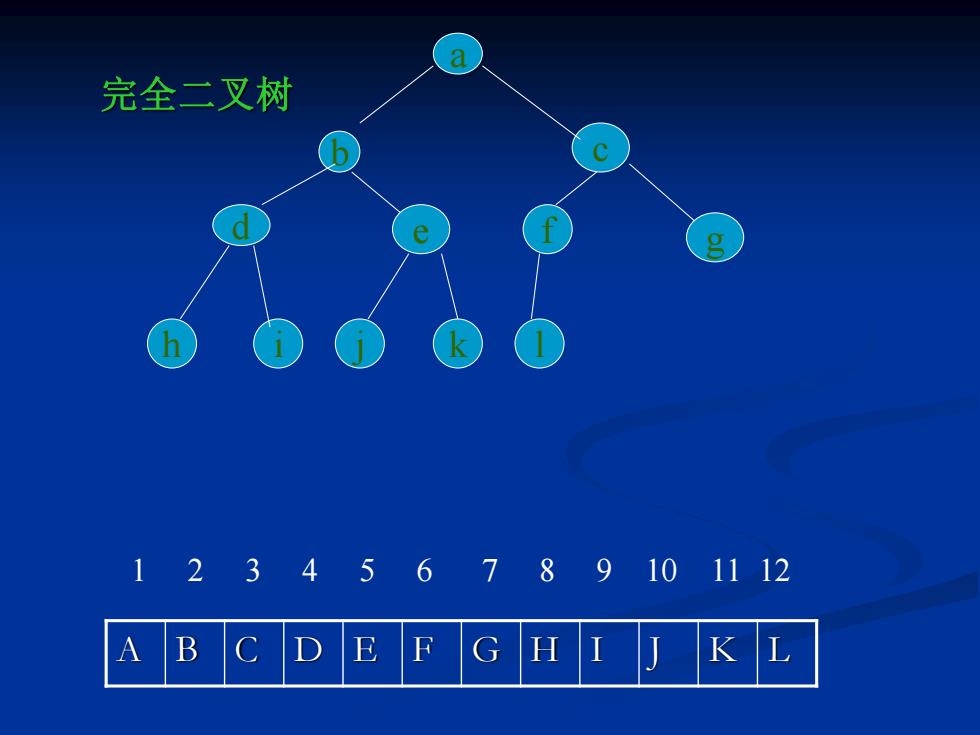
a 完全二叉树 e 123456789101112 A B D
A B C D E F G H I J K L 1 2 3 4 5 6 7 8 9 10 11 12 完全二叉树 a b c d e f g h i j k l