
第六章二叉树 在前面几章里讨论的数据结构都属于线性结构,线性结构的特点是逻辑结构简单,易 于进行查找、插入和删除等操作,其主要用于对客观世界中具有单一的前驱和后继的数据 关系进行描述,而现实中的许多事物的关系并非这样简单,如人类社会的族谱、各种社会 组织机构以及城市交通、通讯等,这些事物中的联系都是非线性的,采用非线性结构进行 描绘会更明确和便利。 所谓非线性结构是指,在该结构中至少存在一个数据元素,有两个或两个以上的直接 前驱(或直接后继)元素。树型结构和图型就是其中十分重要的非线性结构,可以用来描 述客观世界中广泛存在的层次结构和网状结构的关系,如前面提到的族谱、城市交通等。 在本书的第六、七、八章将重点讨论这两类非线性结构的有关概念、存储结构、在各种存 储结构上所实施的一些运算以及有关的应用实例。 本章对树型结构中最简单、应用十分广泛的二叉树结构进行讨论。 6.1定义与性质 6.1.1二叉树的基本概念 1.二叉树 二叉树(Binary Tree)是个有限元素的集合,该集合或者为空、或者由一个称为根(root) 的元素及两个不相交的、被分别称为左子树和右子树的二叉树组成。当集合为空时,称该 二叉树为空二叉树。在二叉树中,一个元素也称作一个结点。 二叉树是有序的,即若将其左、右子树颠倒,就成为另一棵不同的二叉树。即使树中 结点只有一棵子树,也要区分它是左子树还是右子树。因此二叉树具有五种基本形态,如 图6.1所示。 左子树 左子树 左子树》 、左子树 (a) (b) (e) (d) 图6.1二叉树的五种基本形态 103
103 第六章 二叉树 在前面几章里讨论的数据结构都属于线性结构,线性结构的特点是逻辑结构简单,易 于进行查找、插入和删除等操作,其主要用于对客观世界中具有单一的前驱和后继的数据 关系进行描述,而现实中的许多事物的关系并非这样简单,如人类社会的族谱、各种社会 组织机构以及城市交通、通讯等,这些事物中的联系都是非线性的,采用非线性结构进行 描绘会更明确和便利。 所谓非线性结构是指,在该结构中至少存在一个数据元素,有两个或两个以上的直接 前驱(或直接后继)元素。树型结构和图型就是其中十分重要的非线性结构,可以用来描 述客观世界中广泛存在的层次结构和网状结构的关系,如前面提到的族谱、城市交通等。 在本书的第六、七、八章将重点讨论这两类非线性结构的有关概念、存储结构、在各种存 储结构上所实施的一些运算以及有关的应用实例。 本章对树型结构中最简单、应用十分广泛的二叉树结构进行讨论。 6.1 定义与性质 6.1.1 二叉树的基本概念 1.二叉树 二叉树(Binary Tree)是个有限元素的集合,该集合或者为空、或者由一个称为根(root) 的元素及两个不相交的、被分别称为左子树和右子树的二叉树组成。当集合为空时,称该 二叉树为空二叉树。在二叉树中,一个元素也称作一个结点。 二叉树是有序的,即若将其左、右子树颠倒,就成为另一棵不同的二叉树。即使树中 结点只有一棵子树,也要区分它是左子树还是右子树。因此二叉树具有五种基本形态,如 图 6.1 所示。 (a) (b) (c) (d) (e) 图 6.1 二叉树的五种基本形态 Ф 左子树 左子树 左子树 左子树
2.二叉树的相关概念 (1)结点的度。结点所拥有的子树的个数称为该结点的度。 (2)叶结点。度为0的结点称为叶结点,或者称为终瑞结点, (3)分枝结点。度不为0的结点称为分支结点,或者称为非终端结点。一棵树的结点 除叶结点外,其余的都是分支结点。 (4)左孩子、右孩子、双亲。树中一个结点的子树的根结点称为这个结点的孩子。这 个结点称为它孩子结点的双亲。具有同一个双亲的孩子结点互称为兄弟。 (5)路径、路径长度。如果一棵树的一串结点n,也,nk有如下关系:结点n是n4 的父结点(1≤i<k),就把n12,.n,称为一条由n至n,的路径。这条路径的长度是k-l。 (6)祖先、子孙。在树中,如果有一条路径从结点M到结点N,那么M就称为N 的祖先,而N称为M的子孙 (7)结点的层数。规定树的根结点的层数为1,其余结点的层数等于它的双亲结点的 层数加1。 (8)树的深度。树中所有结点的最大层数称为树的深度。 (9)树的度。树中各结点度的最大值称为该树的度。 (10)满二叉树。 在一棵二叉树中,如果所有分支结点都存在左子树和右子树,并且所有叶子结点都在 同一层上,这样的一棵二叉树称作满二叉树.如图6.2所示,(a)图就是一棵满二叉树,(b) 图则不是满二叉树,因为,虽然其所有结点要么是含有左右子树的分支结点,要么是叶子 结点,但由于其叶子未在同一层上,故不是满二叉树。 01 (B2 B 03 64 (E5 6©7 4 E 5 ①6 ①N ①① 891011 12131415 89 (a一棵满二叉树 ()一棵非满二叉树 图6.2满二叉树和非满二叉树示意图 (11)完全二叉树。 一棵深度为k的有个结点的二叉树,对树中的结点按从上至下、从左到右的顺序进 行编号,如果编号为ⅰ(1≤i≤)的结点与满二叉树中编号为i的结点在二叉树中的位置 相同,则这棵二叉树称为完全二叉树。完全二叉树的特点是:叶子结点只能出现在最下层 104
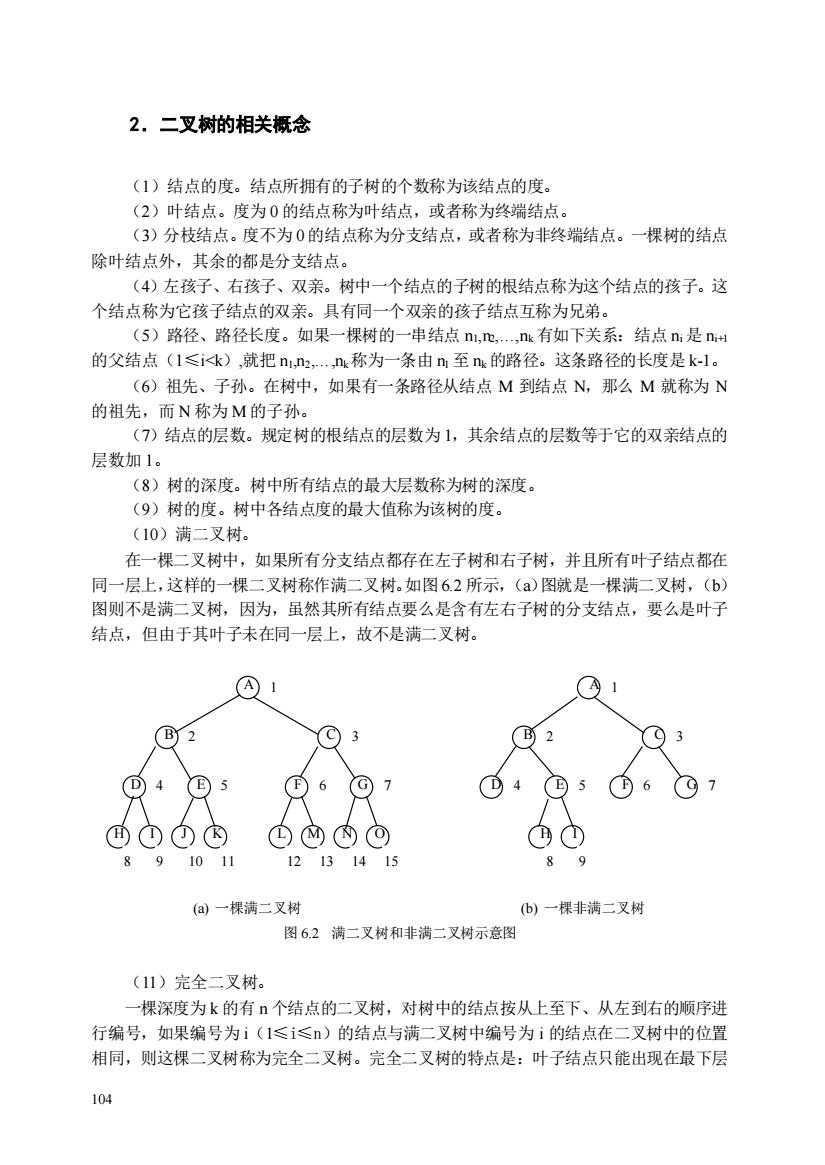
104 2.二叉树的相关概念 (1)结点的度。结点所拥有的子树的个数称为该结点的度。 (2)叶结点。度为 0 的结点称为叶结点,或者称为终端结点。 (3)分枝结点。度不为 0的结点称为分支结点,或者称为非终端结点。一棵树的结点 除叶结点外,其余的都是分支结点。 (4)左孩子、右孩子、双亲。树中一个结点的子树的根结点称为这个结点的孩子。这 个结点称为它孩子结点的双亲。具有同一个双亲的孩子结点互称为兄弟。 (5)路径、路径长度。如果一棵树的一串结点 n1,n2,.,nk 有如下关系:结点 ni 是 ni+1 的父结点(1≤i<k),就把 n1,n2,.,nk称为一条由 n1 至 nk 的路径。这条路径的长度是 k-1。 (6)祖先、子孙。在树中,如果有一条路径从结点 M 到结点 N,那么 M 就称为 N 的祖先,而 N 称为 M 的子孙。 (7)结点的层数。规定树的根结点的层数为 1,其余结点的层数等于它的双亲结点的 层数加 1。 (8)树的深度。树中所有结点的最大层数称为树的深度。 (9)树的度。树中各结点度的最大值称为该树的度。 (10)满二叉树。 在一棵二叉树中,如果所有分支结点都存在左子树和右子树,并且所有叶子结点都在 同一层上,这样的一棵二叉树称作满二叉树。如图 6.2 所示,(a)图就是一棵满二叉树,(b) 图则不是满二叉树,因为,虽然其所有结点要么是含有左右子树的分支结点,要么是叶子 结点,但由于其叶子未在同一层上,故不是满二叉树。 (a) 一棵满二叉树 (b) 一棵非满二叉树 图 6.2 满二叉树和非满二叉树示意图 (11)完全二叉树。 一棵深度为 k 的有 n 个结点的二叉树,对树中的结点按从上至下、从左到右的顺序进 行编号,如果编号为 i(1≤i≤n)的结点与满二叉树中编号为 i 的结点在二叉树中的位置 相同,则这棵二叉树称为完全二叉树。完全二叉树的特点是:叶子结点只能出现在最下层 A B C D E F G H I J K L M N O A B C D E G H F I 1 5 2 3 4 6 7 8 9 10 11 12 13 14 15 1 2 5 3 6 7 8 9 4
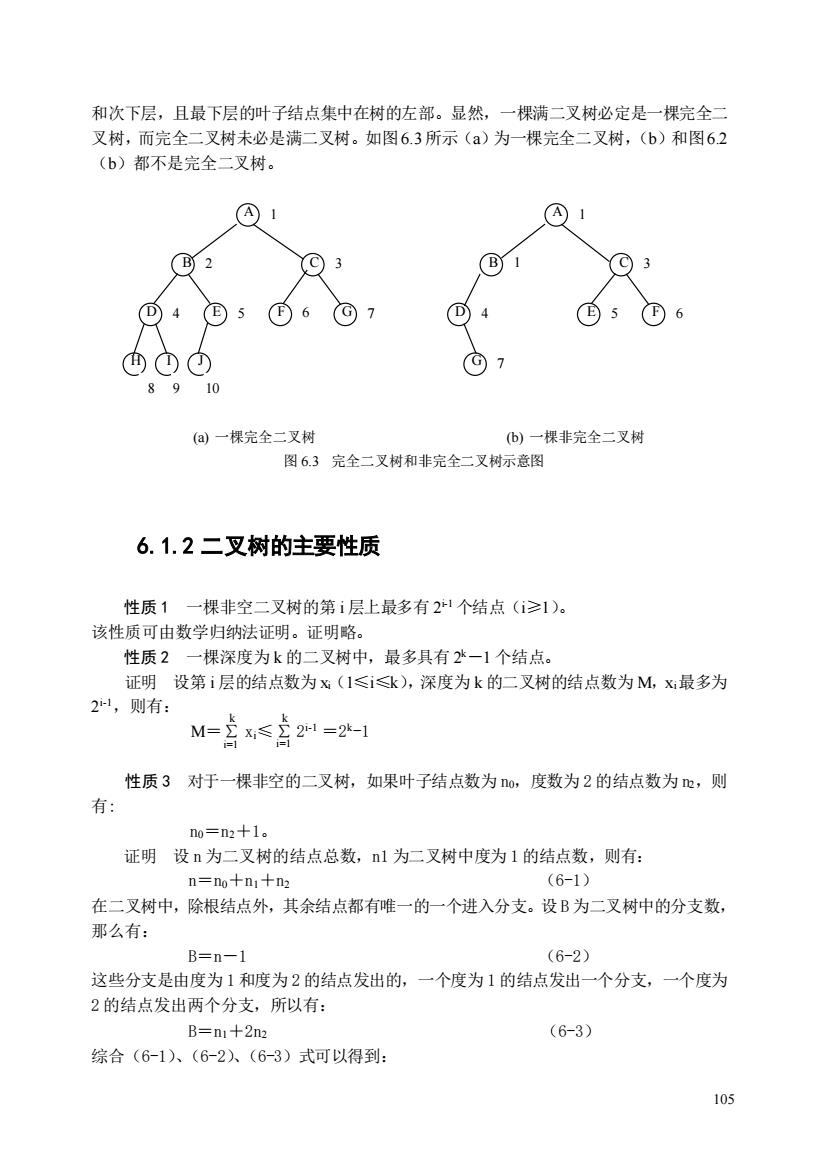
和次下层,且最下层的叶子结点集中在树的左部。显然,一棵满二叉树必定是一棵完全二 叉树,而完全二叉树未必是满二叉树。如图6.3所示(a)为一棵完全二叉树,(b)和图62 (b)都不是完全二叉树。 01 1 (2 ©3 ©3 ⊙4©56 ©7 ©5①6 ®①① ©7 89 10 ()一棵完全二叉树 (b) 一棵非完全二又树 图6.3完全二叉树和非完全二叉树示意图 6.1.2二叉树的主要性质 性质1 一棵非空二叉树的第i层上最多有2个结点(≥1)。 该性质可由数学归纳法证明。证明略。 性质2 一棵深度为k的二叉树中,最多具有2一1个结点。 证明设第i层的结点数为X(1≤i≤k),深度为k的二叉树的结点数为M,x最多为 2,则有: M=2x≤言2=2-1 性质3对于一棵非空的二叉树,如果叶子结点数为o,度数为2的结点数为e,则 有 n0=n2+1 证明设n为二叉树的结点总数,nl为二叉树中度为1的结点数,则有: n=n+n十n (6-1) 在二叉树中,除根结点外,其余结点都有唯一的一个进入分支。设B为二叉树中的分支数, 那么有: B=n-1 (6-2) 这些分支是由度为1和度为2的结点发出的,一个度为1的结点发出一个分支,一个度为 2的结点发出两个分支,所以有: B=n1+2n2 (6-3) 综合(6-1)、(6-2,(6-3)式可以得到:
105 和次下层,且最下层的叶子结点集中在树的左部。显然,一棵满二叉树必定是一棵完全二 叉树,而完全二叉树未必是满二叉树。如图6.3所示(a)为一棵完全二叉树,(b)和图6.2 (b)都不是完全二叉树。 (a) 一棵完全二叉树 (b) 一棵非完全二叉树 图 6.3 完全二叉树和非完全二叉树示意图 6.1.2 二叉树的主要性质 性质 1 一棵非空二叉树的第 i 层上最多有 2 i-1 个结点(i≥1)。 该性质可由数学归纳法证明。证明略。 性质 2 一棵深度为 k 的二叉树中,最多具有 2 k-1 个结点。 证明 设第 i 层的结点数为 xi(1≤i≤k),深度为 k 的二叉树的结点数为 M,xi最多为 2 i-1,则有: M= xi≤ 2 i-1 =2 k-1 性质 3 对于一棵非空的二叉树,如果叶子结点数为 n0,度数为 2 的结点数为 n2,则 有: n0=n2+1。 证明 设 n 为二叉树的结点总数,n1 为二叉树中度为 1 的结点数,则有: n=n0+n1+n2 (6-1) 在二叉树中,除根结点外,其余结点都有唯一的一个进入分支。设 B 为二叉树中的分支数, 那么有: B=n-1 (6-2) 这些分支是由度为 1 和度为 2 的结点发出的,一个度为 1 的结点发出一个分支,一个度为 2 的结点发出两个分支,所以有: B=n1+2n2 (6-3) 综合(6-1)、(6-2)、(6-3)式可以得到: A B C D E F G H I J A B D C E F G 1 2 4 3 5 6 7 8 9 10 1 1 4 3 5 6 7 k ∑ i=1 k ∑ i=1

no=2+1 性质4具有n个结点的完全二叉树的深度k为logn+1。 证明根据完全二叉树的定义和性质2可知,当一棵完全二叉树的深度为k、结点个 数为n时,有 2*-1-1<n≤21 2k-1≤n<2 对不等式取对数,有 k一1≤1ogn<k 由于k是整数,所以有k=[1ogn]+1。 性质5对于具有个结点的完全二叉树,如果按照从上至下和从左到右的顺序对二 叉树中的所有结点从1开始顺序编号,则对于任意的序号为1的结点,有: (1)如果i>1,则序号为i的结点的双亲结点的序号为i/2(/表示整除):如果i= 1,则序号为1的结点是根结点,无双亲结点。 (2)如果2i≤n,则序号为i的结点的左孩子结点的序号为2i:如果2i>n,则序号 为i的结点无左孩子。 (3)如果2i+1≤n,则序号为i的结点的右孩子结点的序号为2i+1:如果2i+1)n, 则序号为1的结点无右孩子。 此外,若对二叉树的根结点从0开始编号,则相应的i号结点的双亲结点的编号为(1 -1)/2,左孩子的编号为21十1,右孩子的编号为2i+2。 此性质可采用数学归纳法证明。证明略。 6.2基本操作与存储实现 6.2.1二叉树的存储 1.顺序存储结构 所谓二叉树的顺序存储,就是用一组连续的存储单元存放二叉树中的结点。一般是按 照二叉树结点从上至下、从左到右的顺序存储。这样结点在存储位置上的前驱后继关系并 不一定就是它们在逻辑上的邻接关系,然而只有通过一些方法确定某结点在逻辑上的前驱 结点和后继结点,这种存储才有意义。因此,依据二叉树的性质,完全二叉树和满二叉树 采用顺序存储比较合适,树中结点的序号可以唯一地反映出结点之间的逻辑关系,这样既 能够最大可能地节省存储空间,又可以利用数组元素的下标值确定结点在二叉树中的位置, 106
106 n0=n2+1 性质 4 具有 n 个结点的完全二叉树的深度 k 为[log2n]+1。 证明 根据完全二叉树的定义和性质 2 可知,当一棵完全二叉树的深度为 k、结点个 数为 n 时,有 2 k-1-1<n≤2 k -1 即 2 k-1≤n<2k 对不等式取对数,有 k-1≤log2n<k 由于 k 是整数,所以有 k=[log2n]+1。 性质 5 对于具有 n 个结点的完全二叉树,如果按照从上至下和从左到右的顺序对二 叉树中的所有结点从 1 开始顺序编号,则对于任意的序号为 i 的结点,有: (1)如果 i>1,则序号为 i 的结点的双亲结点的序号为 i/2(“/”表示整除);如果 i= 1,则序号为 i 的结点是根结点,无双亲结点。 (2)如果 2i≤n,则序号为 i 的结点的左孩子结点的序号为 2i;如果 2i>n,则序号 为 i 的结点无左孩子。 (3)如果 2i+1≤n,则序号为 i的结点的右孩子结点的序号为2i+1;如果 2i+1>n, 则序号为 i 的结点无右孩子。 此外,若对二叉树的根结点从 0 开始编号,则相应的 i 号结点的双亲结点的编号为(i -1)/2,左孩子的编号为2i+1,右孩子的编号为 2i+2。 此性质可采用数学归纳法证明。证明略。 6.2 基本操作与存储实现 6.2.1 二叉树的存储 1.顺序存储结构 所谓二叉树的顺序存储,就是用一组连续的存储单元存放二叉树中的结点。一般是按 照二叉树结点从上至下、从左到右的顺序存储。这样结点在存储位置上的前驱后继关系并 不一定就是它们在逻辑上的邻接关系,然而只有通过一些方法确定某结点在逻辑上的前驱 结点和后继结点,这种存储才有意义。因此,依据二叉树的性质,完全二叉树和满二叉树 采用顺序存储比较合适,树中结点的序号可以唯一地反映出结点之间的逻辑关系,这样既 能够最大可能地节省存储空间,又可以利用数组元素的下标值确定结点在二叉树中的位置
以及结点之间的关系。图6.4给出的图6.3(a)所示的完全二叉树的顺序存储示意。 对于一般的二叉树,如果仍按从上至下和从左到右的顺序将树中的结点顺序存储在 维数组中,则数组元素下标之间的关系不能够反映二叉树中结点之间的逻辑关系,只有增 添一些并不存在的空结点,使之成为一棵完全二叉树的形式,然后再用一维数组顺序存储。 如图6.5给出了一棵一般二叉树改造后的完全二叉树形态和其顺序存储状态示意图。显然, 这种存储对于需增加许多空结点才能将一棵二叉树改造成为一棵完全二叉树的存储时,会 造成空间的大量浪费,不宜用顺序存储结构。最坏的情况是右单支树,如图6.6所示, 棵深度为k的右单支树,只有k个结点,却需分配2一1个存储单元。 ABCDEFGHIJ 数组下标01 6 7 图6.4完全二叉树的顺序存储示意图 ⊙ G B © Q © ò©OO© (a)一棵二叉树 ()改造后的完全二又树 ABC ADE AAAFAAG (@)改造后完全二叉树顺序存储状态 图6.5一般二叉树及其顺序存储示意图 ④ (a)一棵右单支二叉树 )改造后的右单支树对应的完全二叉树 107
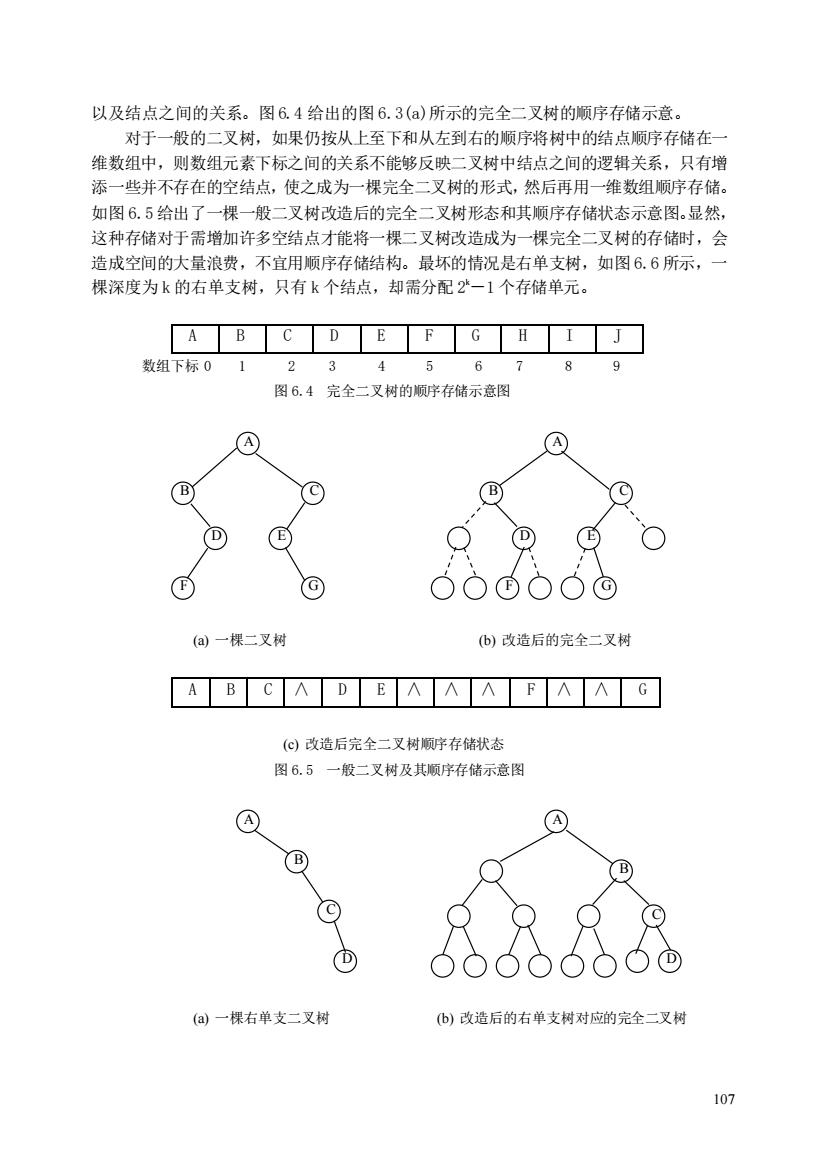
107 以及结点之间的关系。图 6.4 给出的图 6.3(a)所示的完全二叉树的顺序存储示意。 对于一般的二叉树,如果仍按从上至下和从左到右的顺序将树中的结点顺序存储在一 维数组中,则数组元素下标之间的关系不能够反映二叉树中结点之间的逻辑关系,只有增 添一些并不存在的空结点,使之成为一棵完全二叉树的形式,然后再用一维数组顺序存储。 如图 6.5 给出了一棵一般二叉树改造后的完全二叉树形态和其顺序存储状态示意图。显然, 这种存储对于需增加许多空结点才能将一棵二叉树改造成为一棵完全二叉树的存储时,会 造成空间的大量浪费,不宜用顺序存储结构。最坏的情况是右单支树,如图 6.6 所示,一 棵深度为 k 的右单支树,只有 k 个结点,却需分配 2 k-1 个存储单元。 A B C D E F G H I J 数组下标 0 1 2 3 4 5 6 7 8 9 图 6.4 完全二叉树的顺序存储示意图 (a) 一棵二叉树 (b) 改造后的完全二叉树 A B C ∧ D E ∧ ∧ ∧ F ∧ ∧ G (c) 改造后完全二叉树顺序存储状态 图 6.5 一般二叉树及其顺序存储示意图 (a) 一棵右单支二叉树 (b) 改造后的右单支树对应的完全二叉树 A B C D E F G A B D C E F G A C B D D C A B