
第四章数组 数组可以看成是一种特殊的线性表,即线性表中数 据元素本身也是一个线性表 §4.1数组的定义和特点 (a11 a12 au) ★定义 (a21 a22 心 ★数组特点 数组结构固定 数据元素同构 ★数组运算 必给定一组下标,存取相应的数据元素 给定一组下标,修改数据元素的值
第四章 数组 数组可以看成是一种特殊的线性表,即线性表中数 据元素本身也是一个线性表 §4.1 数组的定义和特点 定义 = m m mn n n m n a a a a a a a a a A . . . . . . . . . . . 1 2 21 22 2 11 12 1 数组特点 ❖数组结构固定 ❖数据元素同构 数组运算 ❖给定一组下标,存取相应的数据元素 ❖给定一组下标,修改数据元素的值 ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )
§4.2数组的顺序存储结尥 ★次) 0 a11 按列序为主序存放 a24 。n■量量■量 m- am1 m a12 a11 a12 a22 a21 a22 。●●●●●●● 220 造■道■■■面 am2 &m1 am2 ·●●●0. 8m0 ain a20 Loc(aij)=Loc(a)+[(j-1)m+(i-1)]*I 多”进进想数装 m*n-1 amn
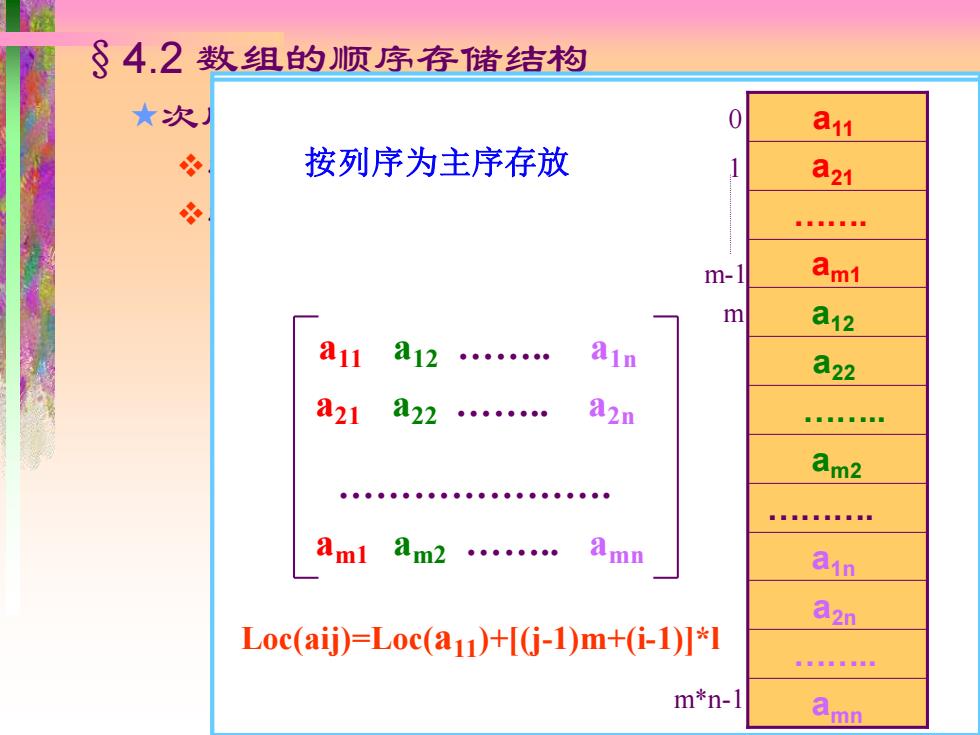
§4.2 数组的顺序存储结构 次序约定 ❖以行序为主序 ❖以列序为主序 a11 a12 . a1n a21 a22 . a2n am1 am2 . amn . Loc( aij)=Loc(a11)+[(i-1)n+(j-1)]*l 按行序为主序存放 amn . am2 am1 . a2n . a22 a21 a1n . a12 0 a11 1 n-1 m*n-1 n 按列序为主序存放 0 1 m-1 m*n-1 m amn . a2n a1n . am2 . a22 a12 am1 . a21 a11 a11 a12 . a1n a21 a22 . a2n am1 am2 . amn . Loc(aij)=Loc(a11)+[(j-1)m+(i-1)]*l
§4.3矩阵的压缩存储 ★对称矩阵 a11 a12. 810 a21 a22.a2n 。0.0e。●s●。e00●0●● Anl an2 ●●●●●●9● Ann 按行序为主序: all a21 a22 a31 a32 anl ann k=0 1234 n(n-1)/2 n(n+1)/2-1 ii-1)/2+j-1,i≥j k= j(U-1)/2+i-1,i<j
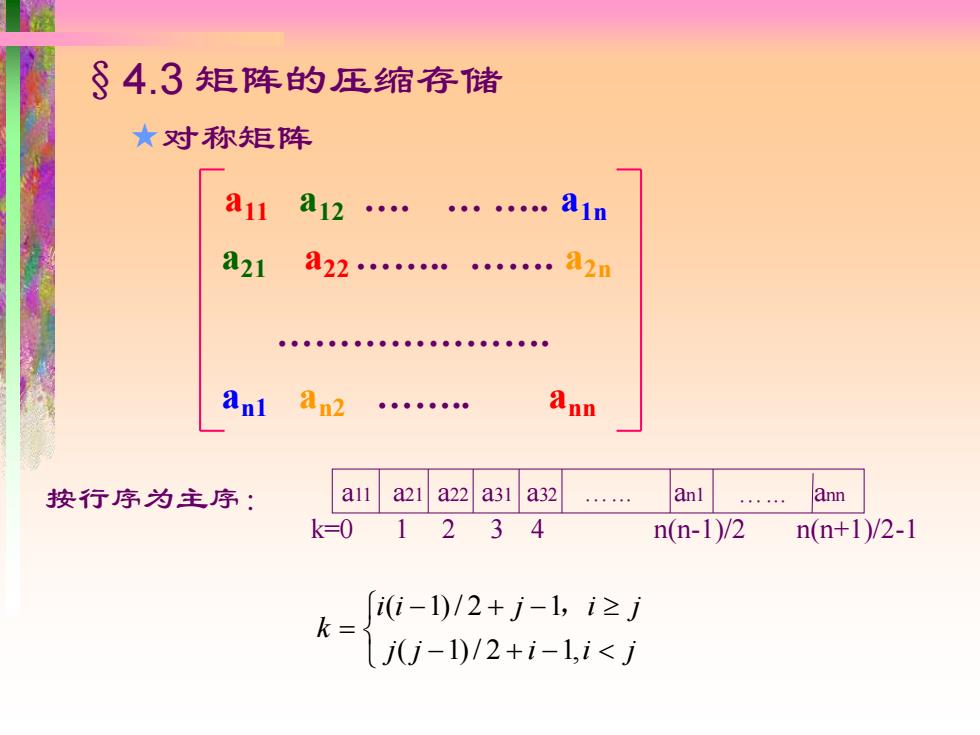
§4.3 矩阵的压缩存储 对称矩阵 − + − − + − = j j i i j i i j i j k ( 1)/ 2 1, ( 1)/ 2 1, a11 a12 . . . a1n a21 a22. . a2n an1 an2 . ann . a11 a21 a22 a31 a32 . an1 . ann k=0 1 2 3 4 n(n-1)/2 n(n+1)/2-1 按行序为主序:

★三角矩阵 a11 0 a21 a22 0. 0 Anl an2 an3. 3n0 按行序为主序: all a21a22a31a32 anl ann k=0 1234 n(n-1)/2 n(n+1)/2-1 Loc(aij)-Loe()D+-1)
三角矩阵 a11 0 0 . 0 a21 a22 0 . 0 an1 an2 an3. ann . 0 Loc(aij)=Loc(a11)+[( +(j-1)]*l i(i-1) 2 a11 a21 a22 a31 a32 . an1 . ann k=0 1 2 3 4 n(n-1)/2 n(n+1)/2-1 按行序为主序:

★对角矩阵 a11 a120 821 a22 a23 0 a32 a33 a340. 0 0 0.an-1,n-2 an-1,n-1 an-1,n 0 0 .ann-1 Ann. 按行序为主序: all a12 a21a22a23 g。, ann-1 ann k=0 1234 n(n-1)/2 n(n+1)/2-1 L0c(aij)=Loc(a1u)+2(i-1)+(j-1)
对角矩阵 a11 a12 0 . . 0 a21 a22 a23 0 . 0 0 0. an-1,n-2 an-1,n-1 an-1,n 0 0 . .an,n-1 ann. 0 a32 a33 a34 0 . 0 . Loc(aij)=Loc(a11)+2(i-1)+(j-1) a11 a12 a21 a22 a23 . . ann-1 ann k=0 1 2 3 4 n(n-1)/2 n(n+1)/2-1 按行序为主序: