
■ 结点的层次:从根开始定义,根为第一层,根的 孩子为第二层。若某个结点在第层,则其子树的 根就在第1+1层。双亲在同一层的结点互为堂兄弟。 树中结点的最大层次称为树的深度或高度。 有序树:如果该树中结点的各子树看成从左至右 是有次序的,则该树称为有序树。否则称为无序 树 森林:是m(m>=0)棵互不相交的树的集合。对 树中每个结点而言,其子树的集合即为森林。 由 此,可以森林和树相互递归的定义来描述树。 Tree=(root,),其中F是m棵树的森林。 F=(T1,T2,T3.Tm),其中T称做根root的第i棵子树
◼ 结点的层次:从根开始定义,根为第一层,根的 孩子为第二层。若某个结点在第l层,则其子树的 根就在第l+1层。双亲在同一层的结点互为堂兄弟。 树中结点的最大层次称为树的深度或高度。 ◼ 有序树:如果该树中结点的各子树看成从左至右 是有次序的,则该树称为有序树。否则称为无序 树。 ◼ 森林:是m(m>=0)棵互不相交的树的集合。对 树中每个结点而言,其子树的集合即为森林。由 此,可以森林和树相互递归的定义来描述树。 Tree=(root, F),其中F是m棵树的森林。 F=(T1,T2,T3.Tm),其中Ti称做根root的第i棵子树

6.2二叉树 二叉树在树结构的应用中起着非常重要的作 用,因为对二叉树的许多操作算法简单,而任何 树都可以与二叉树相互转换,这样就解决了树的 存储结构及其运算中存在的复杂性。 62.1二叉树的定义 定义:二叉树是由n(n>=0)个结点的有限集合构 成,此集合或者为空集 , 或者由一个根结点及两 棵互不相交的左右子树组成,并且左右子树都是 二叉树,且次序不能任意颠倒。 这也是一个递归定义。二叉树可以是空集合 根可以有空的左子树或空的右子树。二叉树不是 树的特殊情况,它们是两个概念
6.2 二叉树 二叉树在树结构的应用中起着非常重要的作 用,因为对二叉树的许多操作算法简单,而任何 树都可以与二叉树 相互转换,这样就解决了树的 存储结构及其运算中存在的复杂性。 6.2.1 二叉树的定义 定义:二叉树是由n(n>=0)个结点的有限集合构 成,此集合或者为空集,或者由一个根结点及两 棵互不相交的左右子树组成,并且左右子树都是 二叉树,且次序不能任意颠倒。 这也是一个递归定义。二叉树可以是空集合, 根可以有空的左子树或空的右子树。二叉树不是 树的特殊情况,它们是两个概念
二叉树结点的子树要区分左子树和右子树,即使只有 一棵子树也要进行区分,说明它是左子树,还是右子 树。这是二叉树与树的最主要的差别。图6.8列出二 差树的5种基本形态,图6.8(C)和图6.8(d)是不同 的两棵二叉树。 B (a) (b) 根和空的 (c) (d) (e) 空二叉树 左右子树 根和左子树 根和右子树 根和左右子树 图6.8二叉树的5种形式
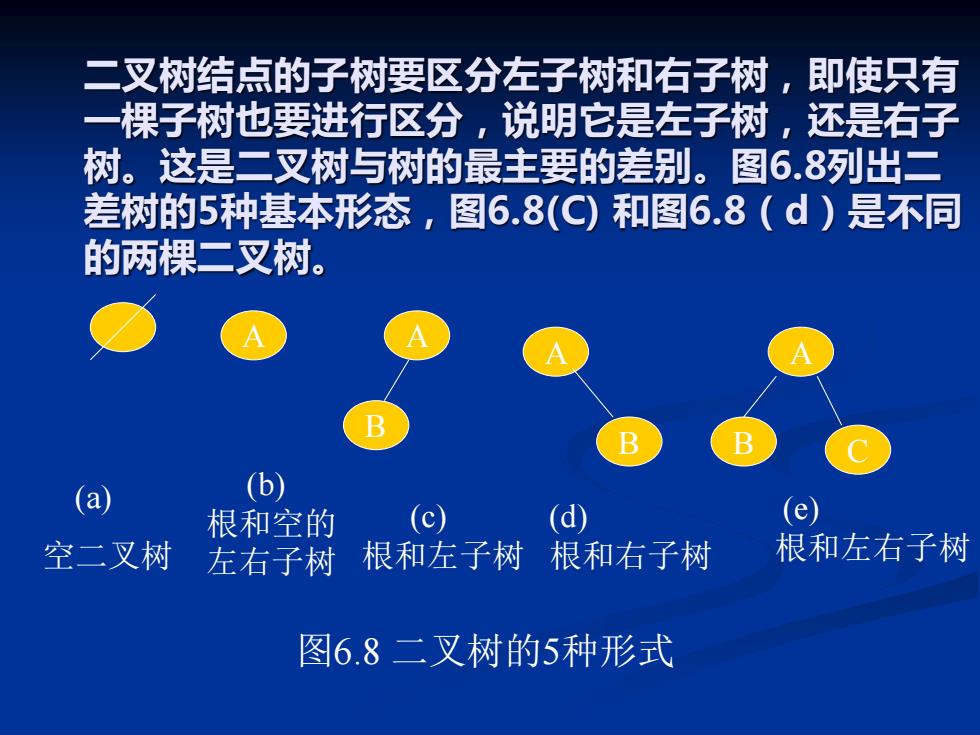
二叉树结点的子树要区分左子树和右子树,即使只有 一棵子树也要进行区分,说明它是左子树,还是右子 树。这是二叉树与树的最主要的差别。图6.8列出二 差树的5种基本形态,图6.8(C) 和图6.8(d)是不同 的两棵二叉树。 (a) 空二叉树 A A B A B A B C (b) 根和空的 左右子树 (c) 根和左子树 (d) 根和右子树 (e) 根和左右子树 图6.8 二叉树的5种形式

6.2.2二叉树的性质 二叉树具有下列重要性质: 性质1:在二叉树的第i层上至多有21个结点(>=1)。 采用归纳法证明此性质。 当i=1时,只有一个根结点,21=2°=1,命题成立。 现在假定对于所有的j,1<=j<i,命题成立,即第j层 上至多有21个结点,那么可以证明j=时命题也成 立。由归纳假设可知,第i-1层上至多有22个结点。 由于二叉树每个结点的度最大为2,故在第层上最 大结点数为第-1层上最大结点数的二倍, 即2×2-2=2-1。命题得到证明
6.2.2 二叉树的性质 二叉树具有下列重要性质: 性质1: 在二叉树的第i层上至多有2 i-1个结点(i>=1)。 采用归纳法证明此性质。 当i=1时,只有一个根结点,2 i-1=20 =1,命题成立。 现在假定对于所有的j,1<=j<i,命题成立,即第j层 上至多有2 j-1个结点,那么可以证明j=i时命题也成 立。由归纳假设可知,第i-1层上至多有2 i-2个结点。 由于二叉树每个结点的度最大为2,故在第i层上最 大结点数为第i-1层上最大结点数的二倍, 即2×2 i-2=2 i-1。命题得到证明

性质2:深度为k的二叉树至多有2水-1个结点 (k>=1): 深度为k的二叉树的最大的结点时为二叉树中每层上 的最大结点数之和,由性质1得到每层上的最大结点 数:E11(第层上的最大结点数)=E=12-1=2水- 1 性质3:对任何一棵二叉树,如果其终端结点数为 n0,度为2的结点数为n2,则n0=n2+1。 设二叉树中度为1的结点数为n1,二叉树中总结点数 为N,因为二叉树中所有结点均小于或等于2,所以 有:N=no+n1+n2 (6-1) 再看二叉树中的分支数,除根结点外,其余结点都 有一个进入分支,设B为二叉树中的分支总数,则 有:N=B+1
性质2:深度为k的二叉树至多有2 k-1个结点 (k>=1). 深度为k的二叉树的最大的结点时为二叉树中每层上 的最大结点数之和,由性质1得到每层上的最大结点 数:E k I=1(第i层上的最大结点数)= Ek I=12 i-1=2k – 1 性质3: 对任何一棵二叉树,如果其终端结点数为 n0,度为2的结点数为n2,则n0=n2+1。 设二叉树中度为1的结点数为n1,二叉树中总结点数 为N,因为二叉树中所有结点均小于或等于2,所以 有:N=n0+n1+n2 (6-1) 再看二叉树中的分支数,除根结点外,其余结点都 有一个进入分支,设B为二叉树中的分支总数, 则 有:N=B+1