
第6章树和二叉树 CTree Binary Tree) 二叉树的定义、 6.1 树的基本概念 性质和存储结构 6.2 二叉树 6.3遍历二叉树和线索二叉树 6.4 树和森林 二叉树的运算 6.5 赫夫曼树及其应用
1 第6章 树和二叉树 (Tree & Binary Tree) 6.1 树的基本概念 6.2 二叉树 6.3 遍历二叉树和线索二叉树 6.4 树和森林 6.5 赫夫曼树及其应用 二叉树的定义、 性质和存储结构 二叉树的运算

6.2二叉树 6.2.1二叉树的定义 6.2.2二叉树的性质 6.2.3二叉树的存储结构 为何要重点研究每结点最多只有两个“叉”的树? 二叉树的结构最简单,规律性最强: 可以证明,所有树都能转为唯一对应的二叉树, 不失一般性
2 6.2 二叉树 为何要重点研究每结点最多只有两个 “叉” 的树? ✓ 二叉树的结构最简单,规律性最强; ✓ 可以证明,所有树都能转为唯一对应的二叉树, 不失一般性。 6.2.1 二叉树的定义 6.2.2 二叉树的性质 6.2.3 二叉树的存储结构

6.2.2二叉树的性质 (3+2) 性质1:在二叉树的第层上至多有2-1个结点(>0)。 性质2: 深度为k的二叉树至多有2k1个结点(k>0) 性质3 对于任何一棵二叉树,若2度的结点数有2个,则叶 子数(no)必定为n2+1(即n,n2+1) 对于两种特殊形式的二叉树(满二叉树和完全二叉树) 还特别具备以下2个性质: 性质4:具有n个结点的完全二叉树的深度必为LIog2n」+1 性质5:对完全二叉树,若从上至下、从左至右编号,则 编号为的结点,其左孩子编号必为2,其右孩子编号为 2i+1:其双亲的编号必为2创(i=1时为根,除外)
3 6.2.2 二叉树的性质 (3+2) 性质1: 在二叉树的第i层上至多有2 i-1个结点(i>0)。 性质2: 深度为k的二叉树至多有2 k-1个结点(k>0)。 性质3: 对于任何一棵二叉树,若2度的结点数有n2个,则叶 子数(n0)必定为n2+1 (即n0=n2+1) 对于两种特殊形式的二叉树(满二叉树和完全二叉树), 还特别具备以下2个性质: 性质4: 具有n个结点的完全二叉树的深度必为log2n+1 性质5: 对完全二叉树,若从上至下、从左至右编号,则 编号为i 的结点,其左孩子编号必为2i,其右孩子编号为 2i+1;其双亲的编号必为i/2(i=1 时为根,除外)
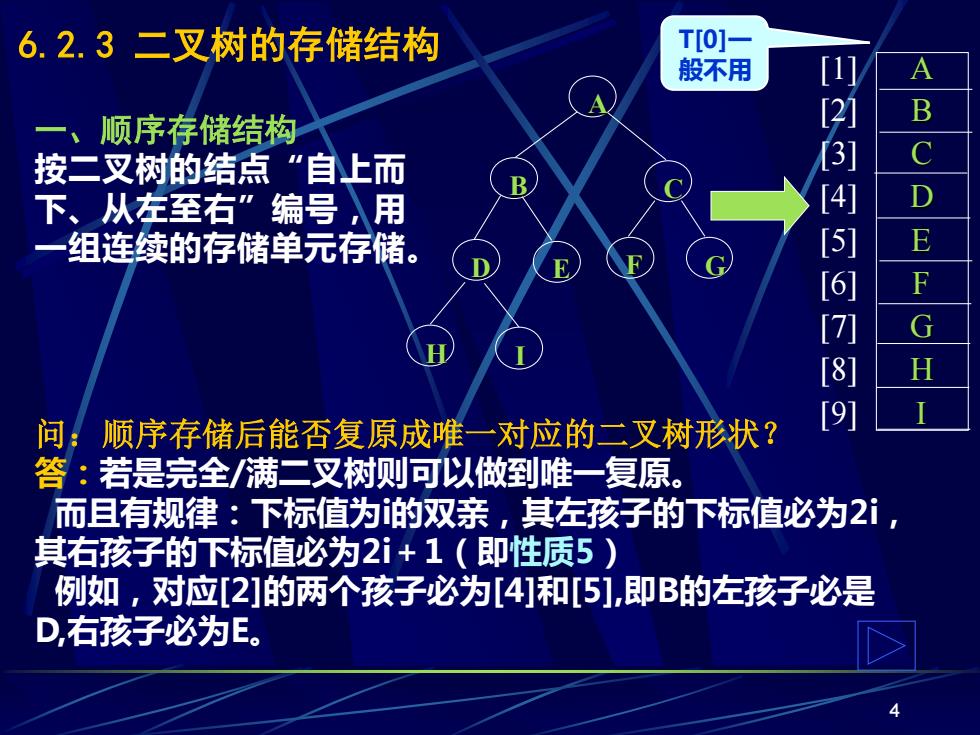
6.2.3二叉树的存储结构 T[O]一 般不用 B 一、 顺序存储结构 按二叉树的结点“自上而 下、从左至右”编号)用 一组连续的存储单元存储。 4567N9 问:顺序存储后能否复原成唯一对应的二叉树形状? 答:若是完全/满二叉树侧可以做到唯一复原。 而且有规律:下标值为的双亲,其左孩子的下标值必为2ⅰ, 其右孩子的下标值必为2ⅰ+1(即性质5) 例如,对应[2]的两个孩子必为[4]和[5],即B的左孩子必是 D,右孩子必为E
4 6.2.3 二叉树的存储结构 一、顺序存储结构 按二叉树的结点“自上而 下、从左至右”编号,用 一组连续的存储单元存储。 A B C D E F G H I [1] [2] [3] [4] [5] [6] [7] [8] [9] A B C E G I D H F 问:顺序存储后能否复原成唯一对应的二叉树形状? 答:若是完全/满二叉树则可以做到唯一复原。 而且有规律:下标值为i的双亲,其左孩子的下标值必为2i, 其右孩子的下标值必为2i+1(即性质5) 例如,对应[2]的两个孩子必为[4]和[5],即B的左孩子必是 D,右孩子必为E。 T[0]一 般不用
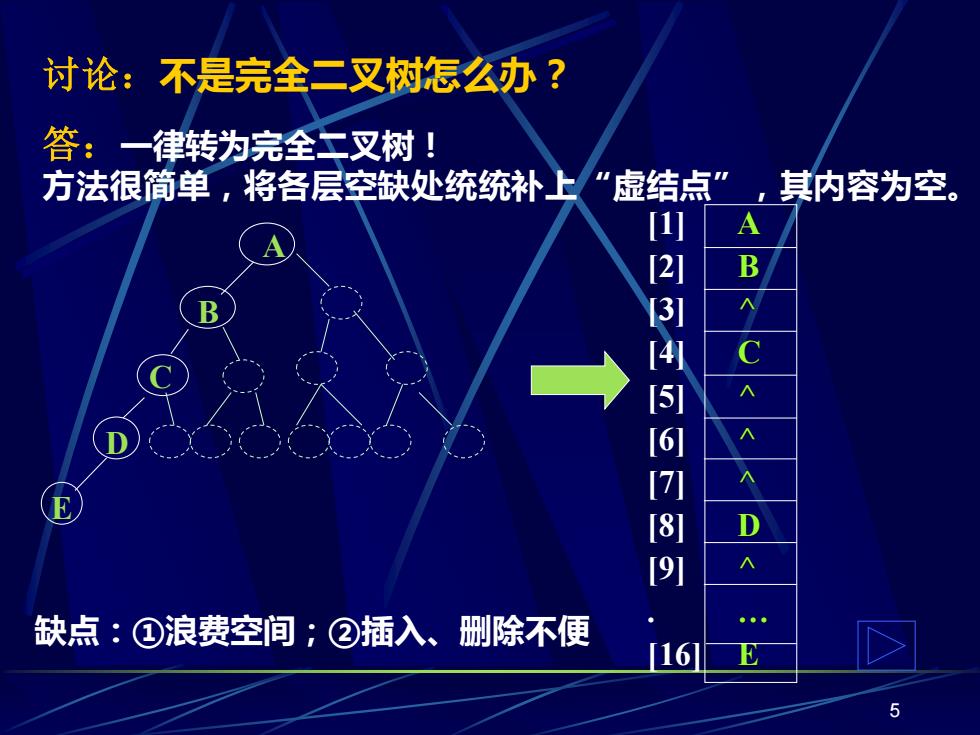
讨论:不是完全二叉树怎么办? 答:一律转为完全二叉树! 方法很简单,将各层空缺处统统补上“虚结点”,其内容为空。 四 23456789 缺点:①浪费空间;②插入、删除不便 6 5
5 讨论:不是完全二叉树怎么办? 答:一律转为完全二叉树! 方法很简单,将各层空缺处统统补上“虚结点” ,其内容为空。 A B ^ C ^ ^ ^ D ^ . E [1] [2] [3] [4] [5] [6] [7] [8] [9] . [16] A B E C D 缺点:①浪费空间;②插入、删除不便