
材料力学课程教案 编号: 课时安排: 1学时教学课型:理论课口实验课口习题课口实践课口其它口 题目(教学章、节或主题):扭转 教学目的要求(分掌握、熟悉、了解三个层次): 1.掌握导出圆轴扭转时横截面上切应力公式的方法。 2.掌握圆轴扭转时横截面上的切应力分布规律,并能熟练地进行圆轴扭转的强度和刚度的 算。 教学重点、难点: 1.圆轴扭转时横截面上的正应力为零,切应力沿半径线性分布,方向垂直于半径。在圆心处切 应力为零,外缘处最大。空心圆截面内缘处有最小的切应力。 2.圆轴扭转时过轴线的纵截面上有分布的切应力,这些切应力的整体效应是构成一个力偶矩。 3.圆轴横截面的极惯性矩包含直径的四次方,抗扭截面系数包含直径的三次方。空心圆截面中 无论是惯性矩,或者是抗扭截面系数,都包含了▣的四次方。 4.对于变扭矩、变截面的圆轴应用积分式计算扭转角。对分段等截面圆轴的组合轴,应分段: 算扭转角,再求和得总扭转角:此类轴的最大切应力不一定是在扭矩最大的横截面上。 5.矩形截面轴的最大切应力出现在长边中点。 教学方式和手段: 通过课件演示、学生交流、师生交流等形式,培养提高学生掌握刚体定轴转动运动的内涵和解决实 际问愿能力。 6
6 材料力学课程教案 编 号: 课时安排: 1 学时 教学课型:理论课□ 实验课□ 习题课□ 实践课□ 其它□ 题目(教学章、节或主题):扭 转 教学目的要求(分掌握、熟悉、了解三个层次): 1. 掌握导出圆轴扭转时横截面上切应力公式的方法。 2. 掌握圆轴扭转时横截面上的切应力分布规律,并能熟练地进行圆轴扭转的强度和刚度的计 算。 教学重点、难点: 1. 圆轴扭转时横截面上的正应力为零,切应力沿半径线性分布,方向垂直于半径。在圆心处切 应力为零,外缘处最大。空心圆截面内缘处有最小的切应力。 2. 圆轴扭转时过轴线的纵截面上有分布的切应力,这些切应力的整体效应是构成一个力偶矩。 3. 圆轴横截面的极惯性矩包含直径的四次方,抗扭截面系数包含直径的三次方。空心圆截面中, 无论是惯性矩,或者是抗扭截面系数,都包含了α 的四次方。 4. 对于变扭矩、变截面的圆轴应用积分式计算扭转角。对分段等截面圆轴的组合轴,应分段计 算扭转角,再求和得总扭转角;此类轴的最大切应力不一定是在扭矩最大的横截面上。 5. 矩形截面轴的最大切应力出现在长边中点。 教学方式和手段: 通过课件演示、学生交流、师生交流等形式,培养提高学生掌握刚体定轴转动运动的内涵和解决实 际问题能力

教学过程:(含复习上节内容、引入新课、中间组织教学以及如何启发思维等) 基本内容: 1.扭转变形和受力特征:在杆件的两端作用等值,反向且作用面垂直于杆件轴线的一对力偶时 杆的任意两个横截面都发生绕轴线的相对转动,这种变形称为扭转变形。 2.外力偶矩的计算,扭矩和扭矩图 (1)M、m、P之间的关系 M。一一外力偶矩(Nm) m一一转速(rmin) P-功率(kw)(1kW=1000Nm5)(马力)(1马力=735.5w 每秒钟内完成的功力 M,20-P M,=9549Pkw nr/min M,h.=7024P冯力 nr/min (2)扭矩和扭矩图 m m X (e) 截面法、平衡方程 ΣM-0 下-Me-0 T=M. 扭矩符号规定:为无论用部分【或部分Ⅱ求出的同一截面上的扭矩不但数值相同且符号相同、扭矩 用右手螺旋定则确定正负号。 3.圆轴扭转时,横截面上的应力、强度条件 (1)横截面上的切应力 分布规律 一点的切应力的大小与该点到圆心的距离成正比,其方向与该的半径相垂直。 教师姓名: 职称: 请插入日期 7
教师姓名: 职称: 请插入日期 7 教学过程:(含复习上节内容、引入新课、中间组织教学以及如何启发思维等) 基本内容: 1.扭转变形和受力特征:在杆件的两端作用等值,反向且作用面垂直于杆件轴线的一对力偶时, 杆的任意两个横截面都发生绕轴线的相对转动,这种变形称为扭转变形。 2.外力偶矩的计算,扭矩和扭矩图 (1)Me、m、 P 之间的关系 Me——外力偶矩(N∙m) n——转速(r/min) P——功率(kW)(1kW=1000N∙m/s)(马力)(1 马力=735.5W) 每秒钟内完成的功力 P n M e 1000 60 2· = 或 P n M e 735.5 60 2· = / min 7024 / min kW 9549 . . n r P M n r P M e N m e N m 马力 = = (2)扭矩和扭矩图 截面法、平衡方程 ΣMx=0 T-Me=0 T=Me 扭矩符号规定:为无论用部分 I 或部分 II 求出的同一截面上的扭矩不但数值相同且符号相同、扭矩 用右手螺旋定则确定正负号。 3.圆轴扭转时,横截面上的应力、强度条件 (1) 横截面上的切应力 分布规律——一点的切应力的大小与该点到圆心的距离成正比,其方向与该的半径相垂直
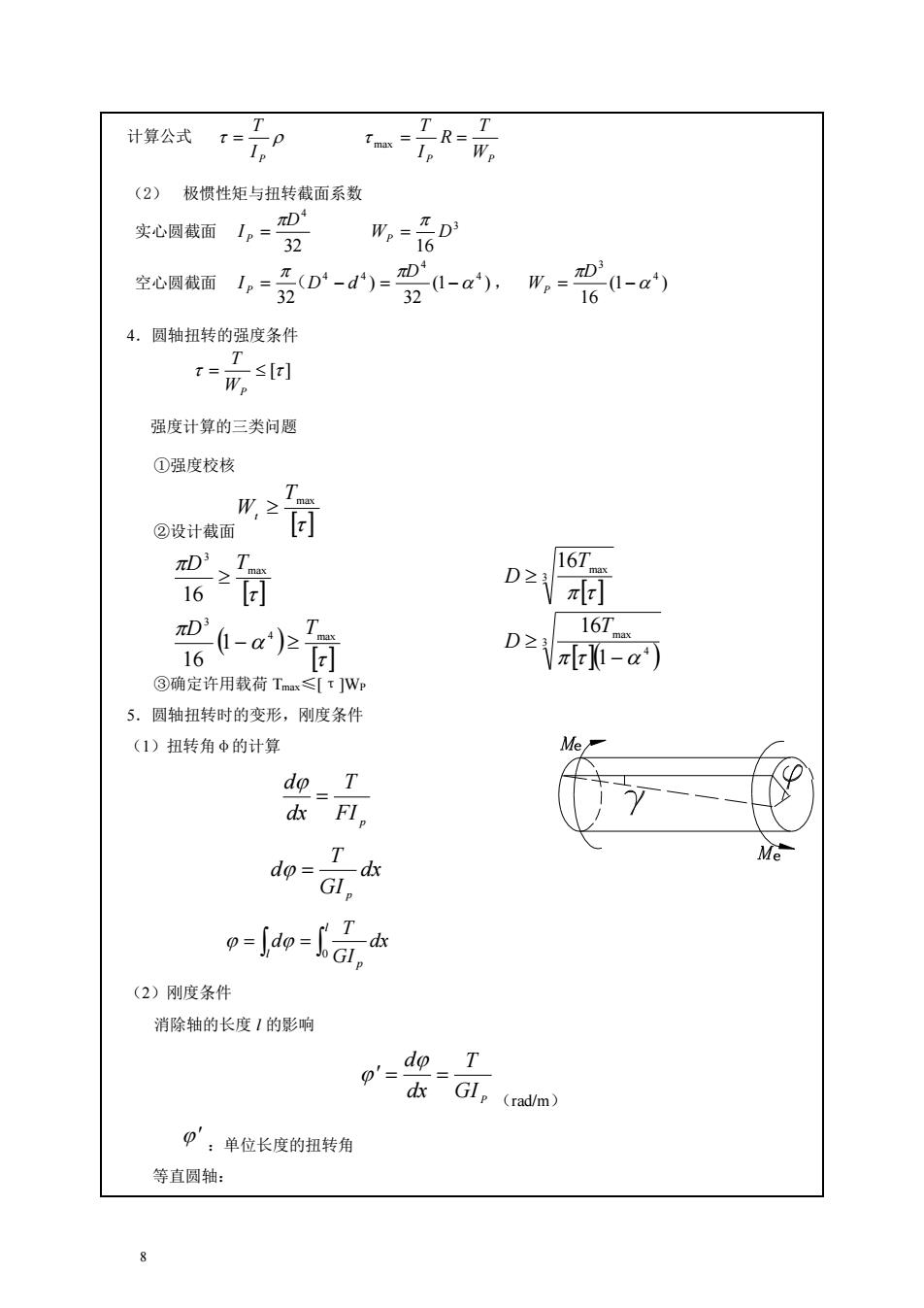
T T 计算公式 1-10 (2)极惯性矩与扭转截面系数 安心图断人:罗 2-a. 160-a 4.圆轴扭转的强度条件 r而阳 强度计算的三类问题 ①强度校核 ②设计截面 aD D≥ 16T D0-u)2 16 D20-a ③确定许用载荷Tmx≤[i]W, 5.圆轴扭转时的变形,刚度条件 (1)扭转角Φ的计算 Me do T dkFI。 T do= 可4 p-o-d (2)刚度条件 消除轴的长度1的影响 T p':单位长度的扭转角 等直圆轴:
8 计算公式 P I T = P WP T R I T max = = (2) 极惯性矩与扭转截面系数 实心圆截面 32 4 D I P = 3 16 WP D = 空心圆截面 (1 ) 32 ) 32 4 4 4 4 = − = − D I P (D d , (1 ) 16 4 3 = − D WP 4.圆轴扭转的强度条件 = [ ] WP T 强度计算的三类问题 ①强度校核 ②设计截面 T max Wt max 3 16 D T 3 16 max T D ( ) 4 max 3 1 16 D T − ( ) 3 4 max 1 16 − T D ③确定许用载荷 Tmax≤[τ]WP 5.圆轴扭转时的变形,刚度条件 (1)扭转角φ的计算 FI p T dx d = dx GI T d p = = = l p l dx GI T d 0 (2)刚度条件 消除轴的长度 l 的影响 GI P T dx d = = (rad/m) :单位长度的扭转角 等直圆轴:
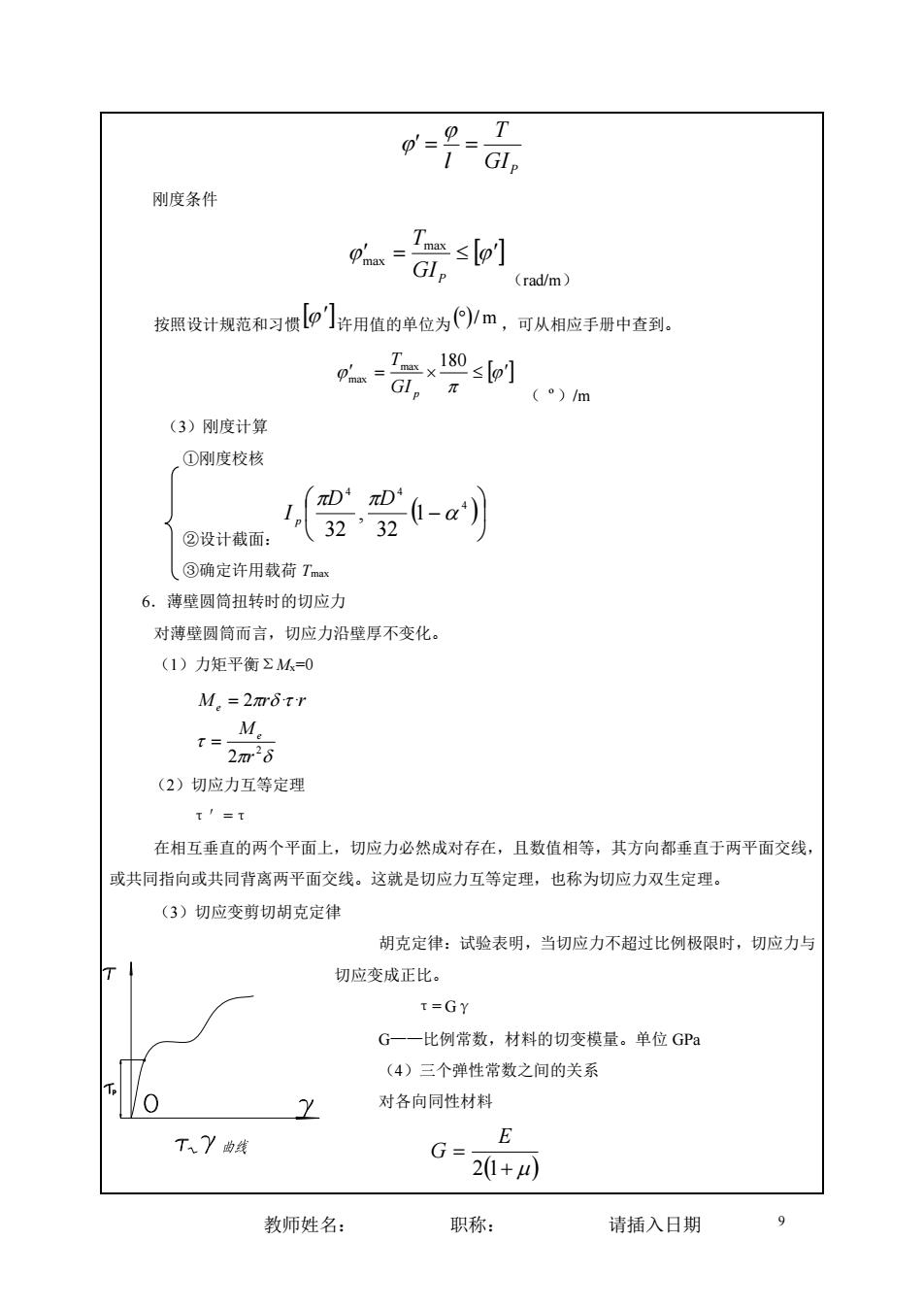
d 刚度条件 器1 (rad/m) 按照设计规范和习惯【p]许用值的单位为(/m,可从相应手册中查到。 ()m (3)刚度计算 ①刚度校核 (D,0-a) ②设计截面 13232 人③确定许用找荷Tm 6.薄壁圆筒扭转时的切应力 对薄壁圆筒而言,切应力沿壁厚不变化。 (1)力矩平衡ΣM-0 M。=2m8tr 污 (2)切应力互等定理 TI=T 在相互垂直的两个平面上,切应力必然成对存在,且数值相等,其方向都垂直于两平面交线 或共同指向或共同背离两平面交线。这就是切应力互等定理,也称为切应力双生定理。 (3)切应变剪切胡克定律 胡克定律:试验表明,当切应力不超过比例极限时,切应力与 切应变成正比。 t=GY G- 比例常数,材料的切变模量。单位GPa (4)三个弹性常数之间的关系 y 对各向同性材料 TY曲线 G- E 201+4) 教师姓名: 职称: 请插入日期
教师姓名: 职称: 请插入日期 9 GIP T l = = 刚度条件 = GI P Tmax max (rad/m) 按照设计规范和习惯 许用值的单位为 ()/ m ,可从相应手册中查到。 = max 180 max GI p T ( º)/m (3)刚度计算 ①刚度校核 ②设计截面: ( ) − 4 4 4 1 32 , 32 D D I p ③确定许用载荷 Tmax 6.薄壁圆筒扭转时的切应力 对薄壁圆筒而言,切应力沿壁厚不变化。 (1)力矩平衡ΣMx=0 2 2 2 ·· r M M r r e e= = (2)切应力互等定理 τ′=τ 在相互垂直的两个平面上,切应力必然成对存在,且数值相等,其方向都垂直于两平面交线, 或共同指向或共同背离两平面交线。这就是切应力互等定理,也称为切应力双生定理。 (3)切应变剪切胡克定律 胡克定律:试验表明,当切应力不超过比例极限时,切应力与 切应变成正比。 τ= Gγ G——比例常数,材料的切变模量。单位 GPa (4)三个弹性常数之间的关系 对各向同性材料 ( + ) = 2 1 E G
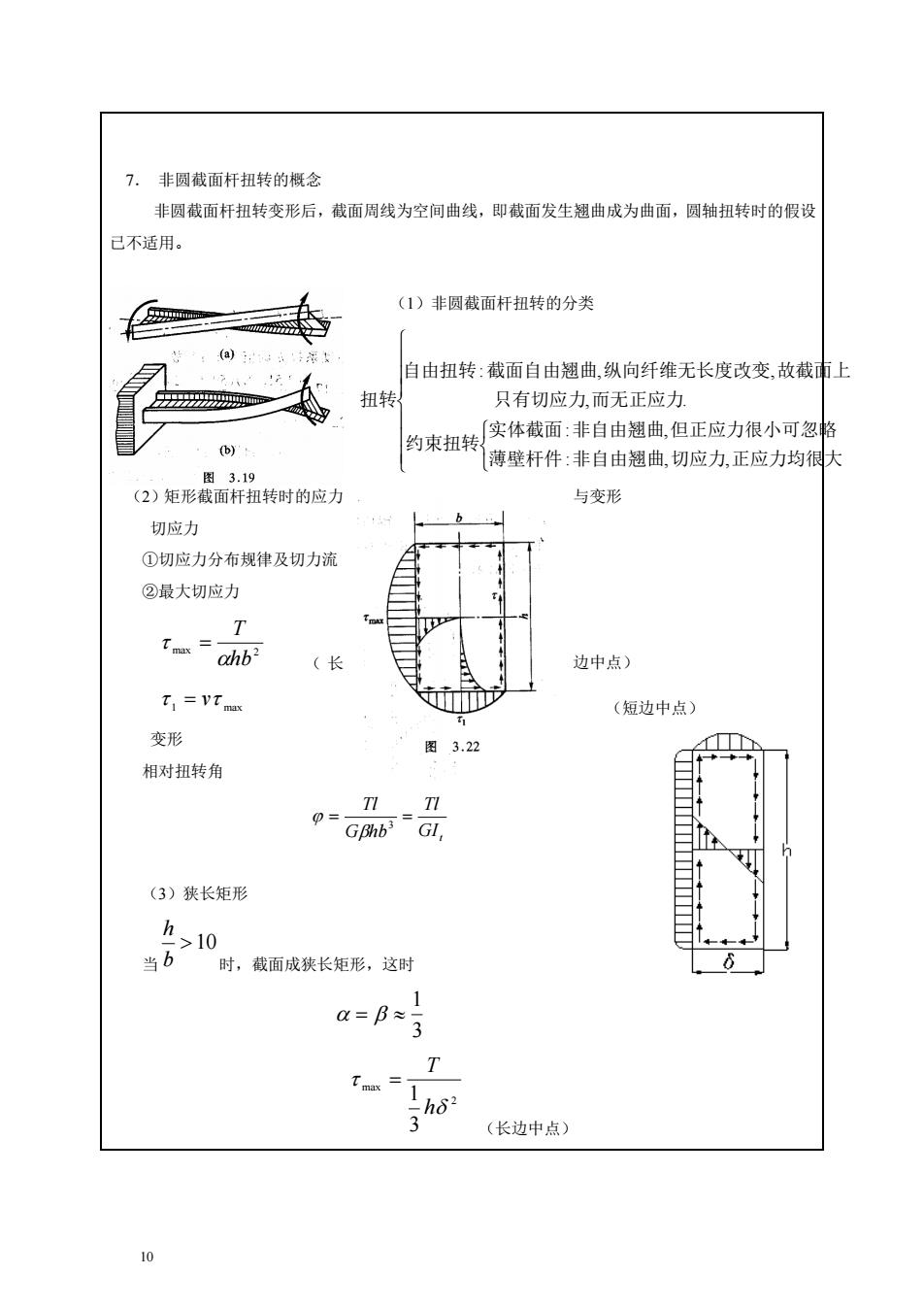
7.非圆截面杆扭转的概念 非圆截面杆扭转变形后,截面周线为空间曲线,即截面发生翘曲成为曲面,圆轴扭转时的假设 己不适用。 (1)非圆截面杆扭转的分类 自由扭转:截面自由翘曲,纵向纤维无长度改变,故截市上 扭转 只有切应力,而无正应力. (b) 约束扭转实体裁面:非自由翘曲但正应力很小可忽格 薄壁杆件:非自由翘曲,切应力,正应力均很大 图3.19 (2)矩形截面杆扭转时的应力 与变形 切应力 ①切应力分布规律及切力流 ②最大切应力 (长 边中点) T =VTmas (短边中点) 变形 图3.2 相对扭转角 品品 (3)狭长矩形 ,10 当b ,截面成狭长矩形,这时 T (长边中点)
10 7. 非圆截面杆扭转的概念 非圆截面杆扭转变形后,截面周线为空间曲线,即截面发生翘曲成为曲面,圆轴扭转时的假设 已不适用。 (1)非圆截面杆扭转的分类 薄壁杆件 非自由翘曲 切应力 正应力均很大 实体截面 非自由翘曲 但正应力很小可忽略 约束扭转 只有切应力 而无正应力 自由扭转 截面自由翘曲 纵向纤维无长度改变 故截面上 扭转 : , , : , , . : , , (2)矩形截面杆扭转时的应力 与变形 切应力 ①切应力分布规律及切力流 ②最大切应力 max 2 hb T = ( 长 边中点) 1 max = v (短边中点) 变形 相对扭转角 GIt Tl G hb Tl = = 3 (3)狭长矩形 当 10 b h 时,截面成狭长矩形,这时 3 1 = 2 max 3 1 h T = (长边中点)