3.2.4用“异或”门实现逻辑函数 第一步求出函数的最简形式。 第二步 将其变换成“异或”表达式。 第三步画出函数表达式对应的逻辑电路图。 例:用异或门实现逻辑电路。 FAB.C,DF2m(1,247,811,13,14CNB00 01 1110 解:第一步: 00 0 01 1 0 由卡诺图可知该逻辑 函数已不能化简。 11 0 10
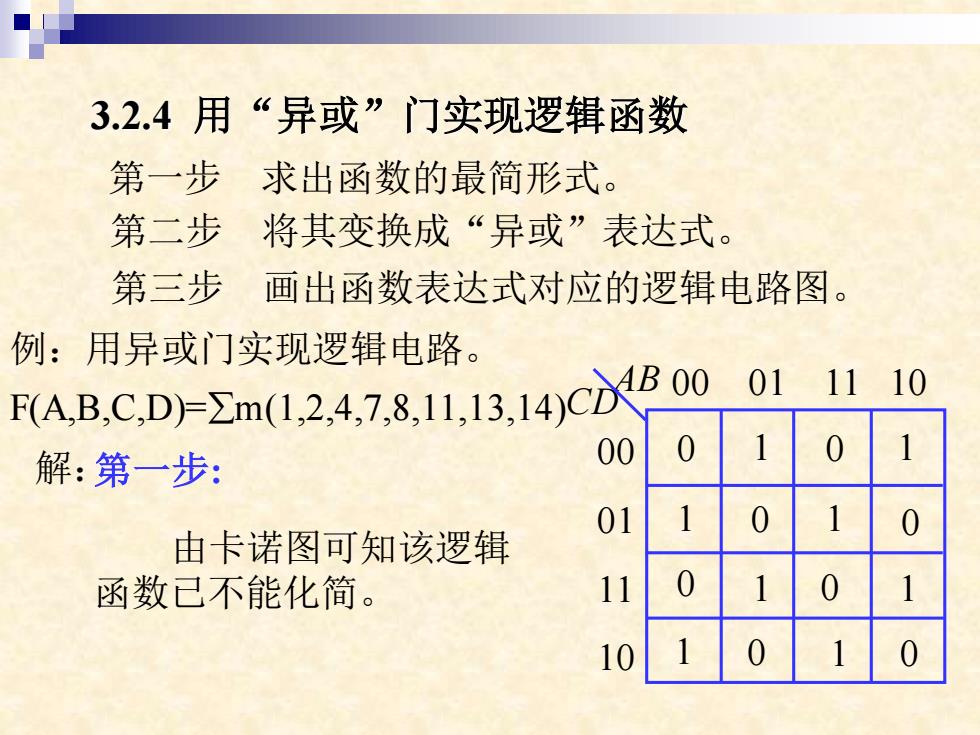
3.2.4 用“异或”门实现逻辑函数 第一步 求出函数的最简形式。 第二步 将其变换成“异或”表达式。 第三步 画出函数表达式对应的逻辑电路图。 例:用异或门实现逻辑电路。 F(A,B,C,D)=m(1,2,4,7,8,11,13,14) 解:第一步: 00 01 11 10 00 01 11 10 AB CD 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 由卡诺图可知该逻辑 函数已不能化简

第二步: F-ABCD+ABCD+ABCD+ABCD+ ABCD+ABCD+ABCD+ABCD =AB(CD+CD)+AB(CD+CD)+ AB(CD+CD)十AB(CD+CD) =(CD+CD)(AB+AB)+(CD+CD)(AB+AB) =(A⊙B)C⊕D)+(A⊕B)COD) =(A⊕B)C⊕D)H(A⊕B(C⊕D) =(A⊕B)⊕(C⊕D)=A⊕B⊕C⊕D A■ 第三步: B
第二步: F=ABCD+ABCD+ABCD+ABCD+ ABCD+ABCD+ABCD+ABCD =AB(CD+CD)+AB(CD+CD)+ AB(CD+CD)+AB(CD+CD) =(CD+CD)(AB+AB)+(CD+CD)(AB+AB) =(A B)(C D)+(A B)(C D) =(A B)(C D)+(A B)(C D) =(A B) (C D) = A B C D 第三步: F A =1 B =1 =1 C D

3.3组合逻辑电路的分析 3.3 分析的任务: 根据给定的组合电路,写出逻辑函数表达式, 并以此来描述它的逻辑功能,确定输入与输出的关 系,必要时对其设计的合理性进行评定。 分析的一般步骤: 第一步:写出给定组合电路的逻辑函数表达式; 第二步:化简逻辑函数表达式: 第三步:根据化简的结果列出真值表; 第四步:功能评述
3.3 组合逻辑电路的分析 分析的任务: 根据给定的组合电路,写出逻辑函数表达式, 并以此来描述它的逻辑功能,确定输入与输出的关 系,必要时对其设计的合理性进行评定。 分析的一般步骤: 第一步:写出给定组合电路的逻辑函数表达式; 第二步:化简逻辑函数表达式; 第三步:根据化简的结果列出真值表; 第四步:功能评述。 3.3
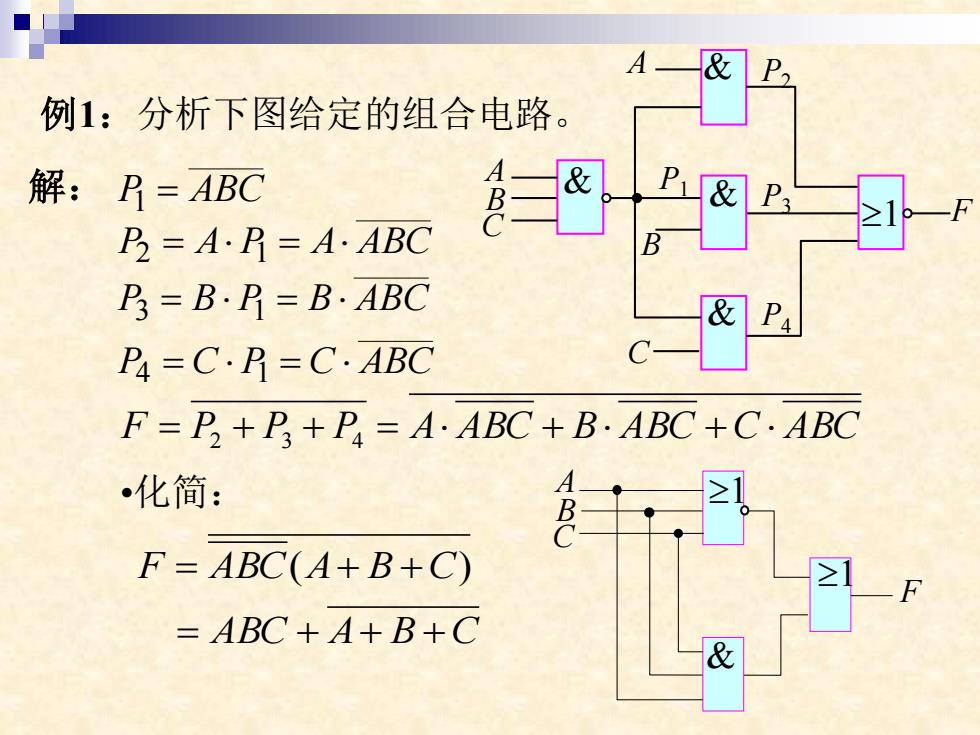
D 例1:分析下图给定的组合电路。 解:B=ABC A P& B=A·B=A·ABC P=B·R=B·ABC P4=C·R=C·ABC F=P+P+P=AABC+B·ABC+C·ABC 化简: F=ABC(A+B+C) =ABC+A+B+C &
解: P1 = ABC P2 = A P1 = A ABC P3 = B P1 = B ABC P4 = C P1 = C ABC F = P2 + P3 + P4 = A ABC + B ABC +C ABC •化简: ABC A B C F ABC A B C = + + + = ( + + ) 1 A C B A C F P1 P2 P3 P4 B & & & & 例1:分析下图给定的组合电路。 & 1 A C B 1 F

•列出真值表 AB C 00 0 1 功能评述 0 0 0 1 0 0 由真值可知,当A、 1 0 B、C取相同值时,F为 0 0 1,否则F为0。所以该 1 1 0 电路是一个“一致性 1 0 0 判定电路"。 1
•列出真值表 •功能评述 由真值可知, 当A、 B、C取相同值时, F为 1, 否则F为0。所以该 电路是一个“一致性 判定电路" 。 A B C F 0 0 0 1 0 0 1 0 0 1 0 0 0 1 1 0 1 0 0 0 1 0 1 0 1 1 0 0 1 1 1 1