南京大学：《电磁学》课程电子教案（教学课件）第八章 电磁感应

电磁学08-02：法拉第电磁感应定律 口从磁矢势A角度看： >构建一任意面元S,其边界为为L: 左手螺旋 右手螺旋 dΦB .dl dt 2=∮EsdI→Es= OA A E=E路+Es=-VU- 8t

电磁学08-02: 法拉第电磁感应定律  从磁矢势 A 角度看：  构建一任意面元 S，其边界为为 L： B S LL L d dd A B dS A dl dl dt dt dt t A E dl E t A EE E U t                                               感 感 静 感

圆电磁学08-02：法拉第电磁感应定律 口感应电动势与感应电场电势【例8.1.7】： >涡旋电场（感生电场）是非保守力场，不能引入电势和电势 差；而静电场是库仑场，可以引入电势和电势差。 > 如果涡旋电场中有导体，其上两点电势差有意义--导体 内与涡旋电场大小相等方向相反的静电场导致两点电势 差。 ∮E.w=0fai=-s V×E库=0 vxE-- t

电磁学08-02: 法拉第电磁感应定律  感应电动势与感应电场电势【例8.1.7】：  涡旋电场(感生电场)是非保守力场，不能引入电势和电势 差；而静电场是库仑场，可以引入电势和电势差。  如果涡旋电场中有导体，其上两点电势差有意义----导体 内与涡旋电场大小相等方向相反的静电场导致两点电势 差。 0 0 L S L B E dl dS E dl t E B E t                             感 库 库 感

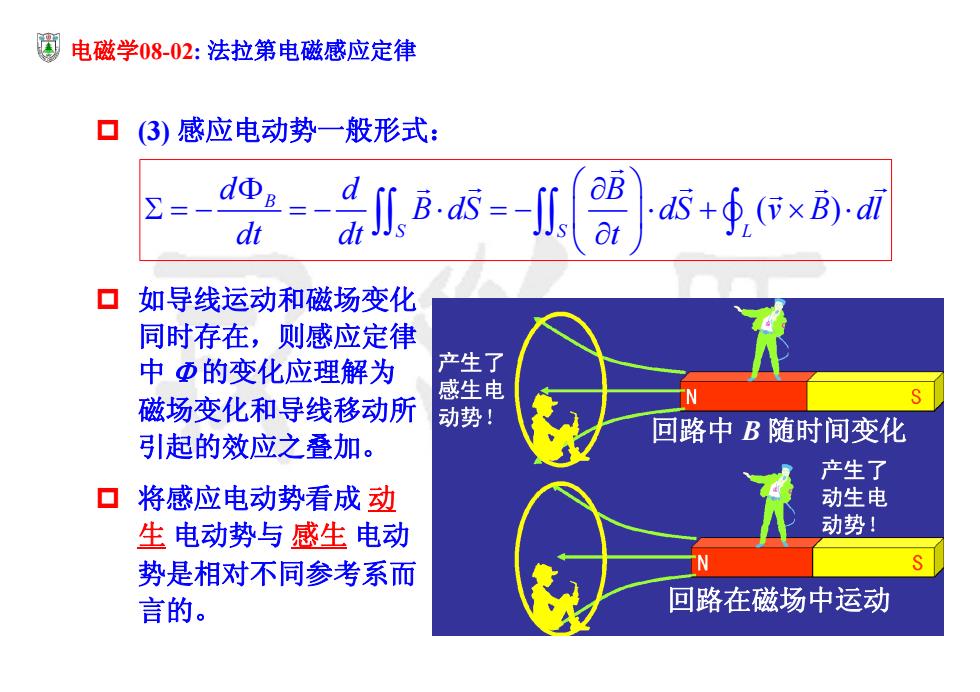
圆电磁学08-02：法拉第电磁感应定律 口3)感应电动势一般形式： s、 dΦ=- 八=八 as+∮(×B)团 口如导线运动和磁场变化 同时存在，则感应定律 中Φ的变化应理解为 产生了 感生电 磁场变化和导线移动所 动势！ 引起的效应之叠加。 回路中B随时间变化 产生了 口将感应电动势看成动 动生电 生电动势与感生电动 动势！ 势是相对不同参考系而 言的。 回路在磁场中运动

电磁学08-02: 法拉第电磁感应定律  (3) 感应电动势一般形式： ( ) B SS L d d B B dS dS v B dl dt dt t                               如导线运动和磁场变化 同时存在，则感应定律 中  的变化应理解为 磁场变化和导线移动所 引起的效应之叠加。  将感应电动势看成 动 生 电动势与 感生 电动 势是相对不同参考系而 言的。 回路中 B 随时间变化 回路在磁场中运动

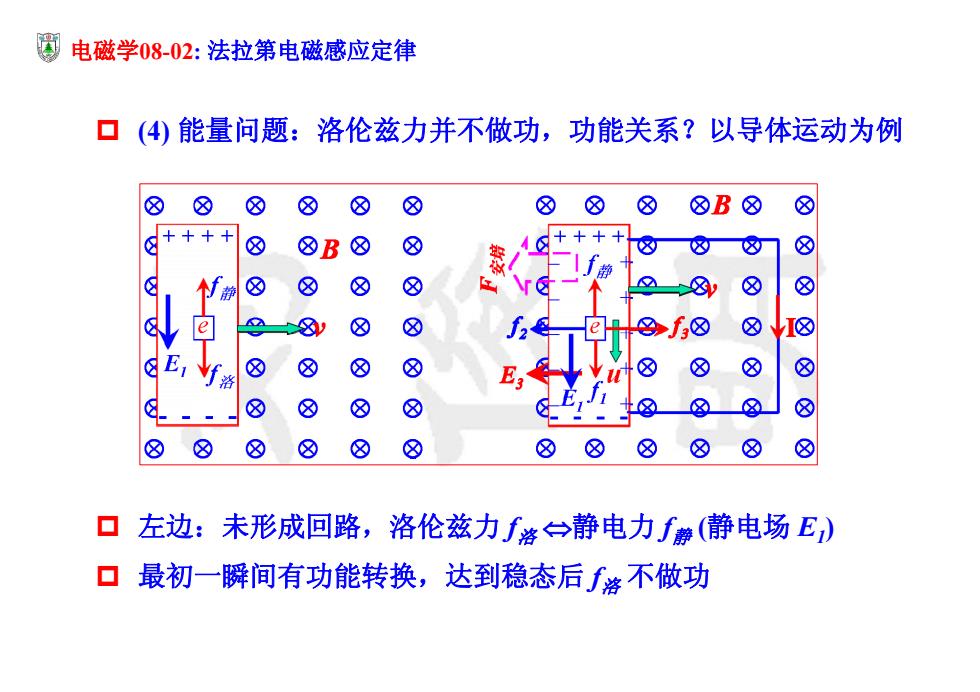
圆电磁学0802：法拉第电磁感应定律 口(4)能量问题：洛伦兹力并不做功，功能关系？以导体运动为例 ⑧ ⑧ ⑧ ⑧ ⑧ ⑧ ⑧ ⑧ ⑧B⑧ ⑧ 区++++ ⑧ ⑧B⑧ ⑧ 4++++ 静 静 ⑧ ⑧ ⑧ ⑧ 8 ⑧ e 8 & 8f8 ⑧I& E ⑧ ⑧ ⑧ ⑧ ⑧ ⑧ ⑧ & ⑧ ⑧ ⑧ ⑧⑧⑧ ⑧ ⑧ ⑧ ⑧ & ⑧⑧ ⑧ ⑧ ▣左边： 未形成回路，洛伦兹力∫洛一静电力∫静（静电场E) 口最初一瞬间有功能转换，达到稳态后∫洛不做功

电磁学08-02: 法拉第电磁感应定律  (4) 能量问题：洛伦兹力并不做功，功能关系？以导体运动为例  左边：未形成回路，洛伦兹力 f洛静电力 f静 (静电场 E1)  最初一瞬间有功能转换，达到稳态后 f洛 不做功

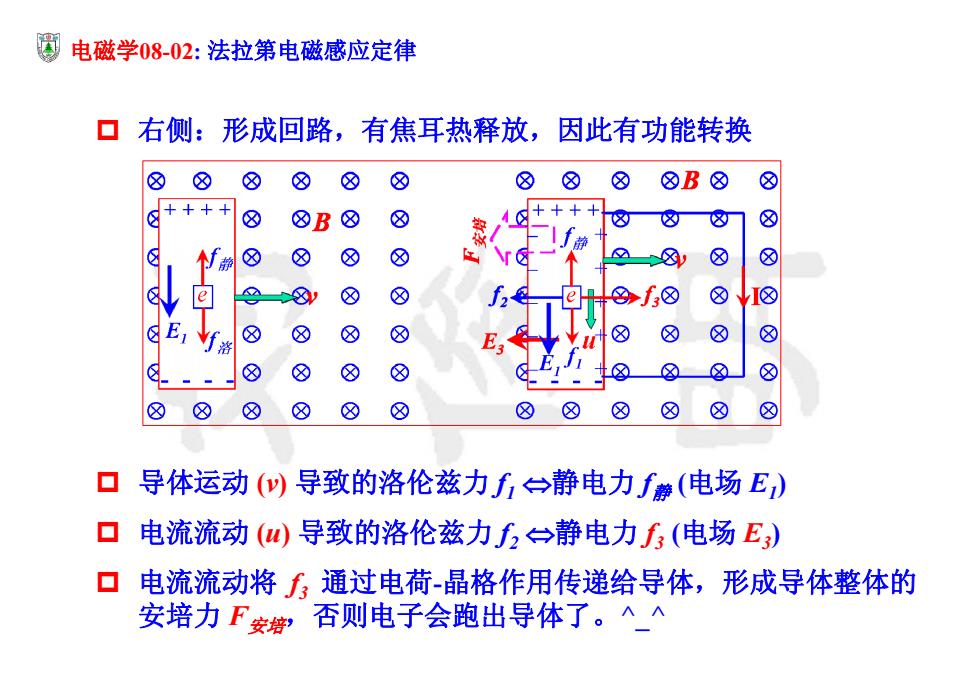
电磁学0802：法拉第电磁感应定律 口右侧：形成回路，有焦耳热释放，因此有功能转换 ⑧⑧ ⑧ ⑧ ⑧ ⑧ 8 ⑧ ⑧ ⑧B⑧ ⑧ &++++ ⑧ &B& ⑧ ⑧ 静 ⑧ ⑧ ⑧ ⑧ ⑧ e @8y ⑧ ⑧ 8f5⑧ ⑧I⑧ ⑧ ⑧ & ⑧ ☒ ⑧ ⑧ ⑧ ⑧ ⑧ ⑧⑧」⑧ ⑧ ⑧ & ⑧ ⑧☒ ⑧ ⑧☒ ⑧ 口导体运动()导致的洛伦兹力f→静电力f静（电场E) 口电流流动(W)导致的洛伦兹力f)一静电力f(电场E) 口电流流动将通过电荷-晶格作用传递给导体，形成导体整体的 安培力F安，否则电子会跑出导体了。人_

电磁学08-02: 法拉第电磁感应定律  右侧：形成回路，有焦耳热释放，因此有功能转换  导体运动 (v) 导致的洛伦兹力 f1 静电力 f静 (电场 E1)  电流流动 (u) 导致的洛伦兹力 f2 静电力 f3 (电场 E3)  电流流动将 f3 通过电荷-晶格作用传递给导体，形成导体整体的 安培力 F安培，否则电子会跑出导体了。^_^