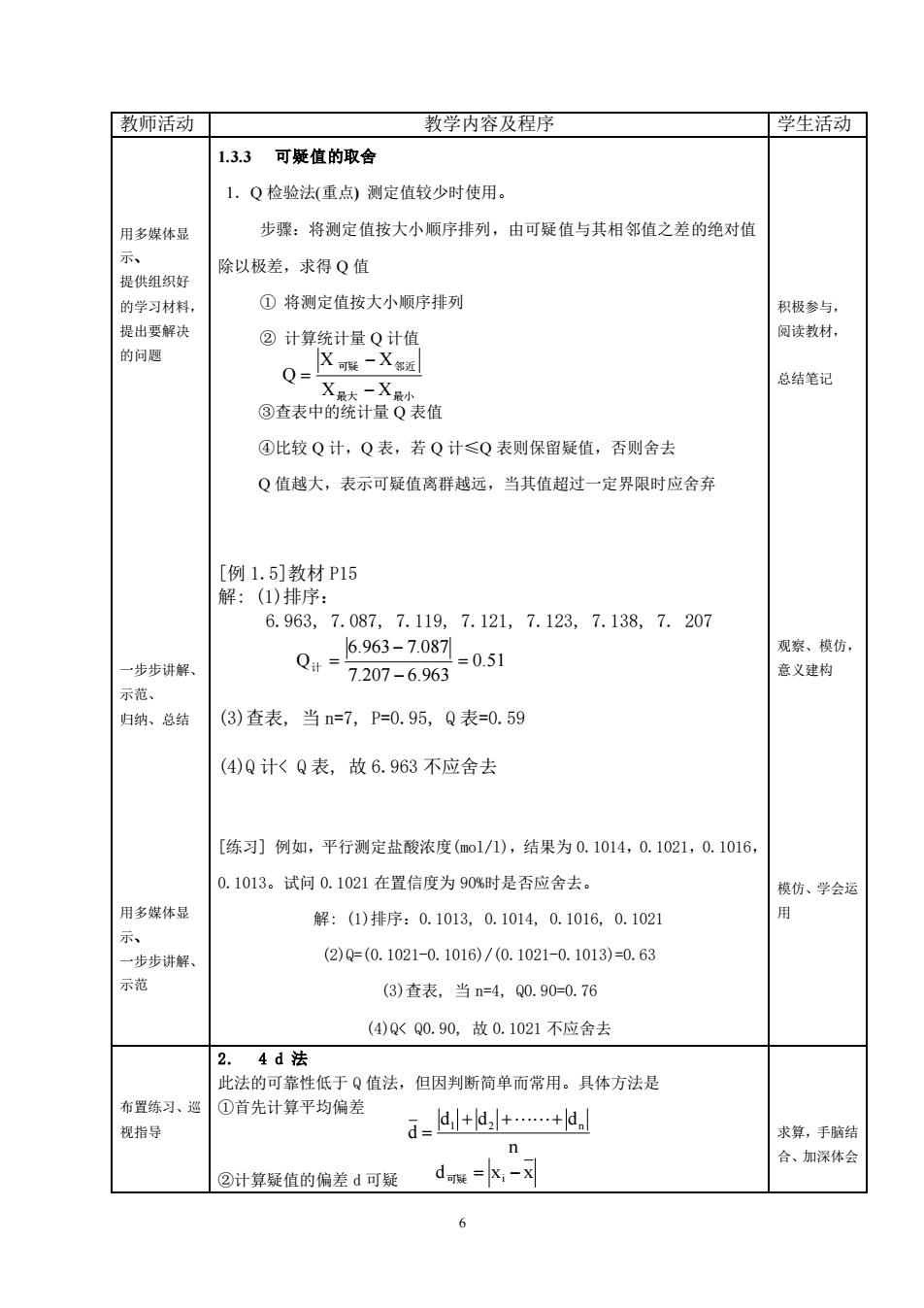
教师活动工 教学内容及程序 学生活动 1.3.3可糜值的取舍 1.Q检验法重点)测定值较少时使用。 用多媒体显 步骤:将测定值按大小顺序排列,由可疑值与其相邻值之差的绝对值 示、 除以极差,求得Q值 提供组织好 的学习材料 ①将测定值按大小顺序排列 积极参与 提出要解决 阅读教材 的向题 总结笔记 X -X ③查表中的统计量Q表值 ④比较Q计,Q表,若Q计≤Q表则保留疑值,否则舍去 Q值越大,表示可疑值离群越远,当其值超过一定界限时应舍弃 [例1.5]教材P15 解:(1)排序: 6.963,7.087,7.119,7.121,7.123,7.138,7.207 6.963-7.087 观黎、模仿 一步步讲解、 示范、 Q+=7207-6,963 =0.51 意义建构 归钠、总结 (3)查表,当n=7,P=0.95,Q表=0.59 (4)Q计<Q表,故6.963不应舍去 [练习]例如,平行测定盐酸浓度(o1/1),结果为0.1014,0.102L1,0.1016 0.1013。试问0.1021在置信度为90%时是否应舍去。 模仿、学会运 多媒体显 解:1)捧序:0.1013,0.1014,0.1016,0.1021 用 示 步步讲解 (2)Q(0.1021-0.1016)/(0.1021-0.1013)=0.63 示范 (3)查表,当n=4,Q0.90=0.76 (4)Q<Q0.90,故0.1021不应舍去 4d法 此法的可靠性低于Q值法,但因判断简单而常用。具体方法是 布置练习、巡 ①首先计算平均偏差 视指导 a-+,++d 求算,手脑结 合、加深体会 ②计算疑值的偏差d可疑 d猴=k-入
6 教师活动 教学内容及程序 学生活动 用多媒体显 示、 提供组织好 的学习材料, 提出要解决 的问题 1.3.3 可疑值的取舍 1.Q 检验法(重点) 测定值较少时使用。 步骤:将测定值按大小顺序排列,由可疑值与其相邻值之差的绝对值 除以极差,求得 Q 值 ① 将测定值按大小顺序排列 ② 计算统计量 Q 计值 ③查表中的统计量 Q 表值 ④比较 Q 计,Q 表,若 Q 计≤Q 表则保留疑值,否则舍去 Q 值越大,表示可疑值离群越远,当其值超过一定界限时应舍弃 积极参与, 阅读教材, 总结笔记 一步步讲解、 示范、 归纳、总结 [例 1.5]教材 P15 解: (1)排序: 6.963, 7.087, 7.119, 7.121, 7.123, 7.138, 7. 207 (3)查表, 当 n=7, P=0.95, Q 表=0.59 (4)Q 计< Q 表, 故 6.963 不应舍去 观察、模仿, 意义建构 用多媒体显 示、 一步步讲解、 示范 [练习] 例如,平行测定盐酸浓度(mol/l),结果为 0.1014,0.1021,0.1016, 0.1013。试问 0.1021 在置信度为 90%时是否应舍去。 解: (1)排序:0.1013, 0.1014, 0.1016, 0.1021 (2)Q=(0.1021-0.1016)/(0.1021-0.1013)=0.63 (3)查表, 当 n=4, Q0.90=0.76 (4)Q< Q0.90, 故 0.1021 不应舍去 模仿、学会运 用 布置练习、巡 视指导 2. 4 d 法 此法的可靠性低于 Q 值法,但因判断简单而常用。具体方法是 ①首先计算平均偏差 ②计算疑值的偏差 d 可疑 求算,手脑结 合、加深体会 最大 最小 可疑 邻近 X X X X Q − − = 0.51 7.207 6.963 6.963 7.087 Q = − − 计 = n d d d d 1 + 2 + + n = d可疑 = xi − x

教师活动 教学内容及程序 学生活动门 ③比较d可疑和d,若d>4d,则舍去可疑值 若d可疑≤4d,则保留可疑值。 [例1.4幻教材P14 1.4系统误差的检验(显著性检验) 建议课后参 系统误差影响准确度,在分析必须检验系统误差是否存在 园《定草分析 系统误差的检验方法 简明教程》 选用组成与试样相近的标准试样来做测定, 崇慧主编北 用多媒体显 京大学出版 示、 ◆若测定结果(区)与标准值(μ)不符,则说明系误差存在 ◆采用标准方法与所选方法测定同一样品。 若两种测定结果(X1,X2 )不符,则说明系统误差存在 1.4.1t检验法 1。平均值与标准值的比较 ①先由下式计算t值 求学生深 t=. 后查阅相关 ②查表1值 资料自学 ③比较t计和1af值 ·若t计>tf 则平均值与标准值存在显著性差异,测定中存在系统 误差 若t计≤t. ,则平均值与真实值μ之间不存在显著性差异 [例1.6P15 「练习1 用分光光度法测定标准物质中的铝的含量。 五次测定结果的平均值(4%)为0.1080,标准偏差为0.0005. 己知铝含量的标准值 问置信度 95%时】 定为00 解:t=.01080-0107×5=224 0.0005 杳表,t0054=278。因t<t0054 故平均值与标准值之间无品著性差异不存在系统误差 1.4,2两组平均值的比较 1.F检验法 通过比较两组数据的方差,以确定它们的精密度之间有无显著性差异。用 统计量F表示 F-S 。F计之F表,则爵数据的精密度布在显若性差异 ·℉计≤F表,则两组数据的精密度不存在显著性差异 [例用两种方法测定同一样品中某组分。 第1法,共测6次,S1=0.055: 第2法,共测4次,S2=0.022。 试问这两种方法的精密度有无显著性差别。 >
7 教师活动 教学内容及程序 学生活动 ③比较 d 可疑和 d,若 d 可疑>4d,则舍去可疑值, 若 d 可疑≤4d,则保留可疑值。 [例 1.4]教材 P14 用多媒体显 示、 要求学生课 后查阅相关 资料自学 1.4 系统误差的检验(显著性检验) 系统误差影响准确度,在分析必须检验系统误差是否存在 系统误差的检验方法 选用组成与试样相近的标准试样来做测定, ◆ 若测定结果( X )与标准值( )不符,则说明系误差存在统 ◆ 采用标准方法与所选方法测定同一样品, 若两种测定结果( )不符,则说明系统误差存在 1.4.1 t 检验法 1.平均值与标准值的比较 ① 先由下式计算 t 值 ② 查表 tα,f 值 ③ 比较 t 计和 tα,f 值, • 若 t 计> tα,f 则平均值与标准值存在显著性差异,测定中存在系统 误差 若 t 计 ≤tα,f ,则 平均值与真实值μ之间不存在显著性差异 [例 1.6] P15 [练习] 用分光光度法测定标准物质中的铝的含量。 五次测定结果的平均值 (Al%)为 0.1080, 标准偏差为 0.0005, 已知铝含量的标准值 (Al%)为 0.1075。 问置信度为 95%时,测定是否可靠? 解: 查表, t0.05,4=2.78。因 t< t0.05,4 故平均值与标准值之间无显著性差异,不存在系统误差 1.4.2 两组平均值的比较 1.F 检验法 通过比较两组数据的方差,以确定它们的精密度之间有无显著性差异。用 统计量 F 表示 • F 计≥F 表,则两组数据的精密度存在显著性差异 • F 计≤F 表,则两组数据的精密度不存在显著性差异 [例]用两种方法测定同一样品中某组分。 第1法,共测6次,S1=0.055; 第2法,共测4次,S2=0.022。 试问这两种方法的精密度有无显著性差别。 建议课后参 阅《定量分析 简明教程》彭 崇慧主编 北 京大学出版 社 x x1, x2 t n S | x μ| = − t n S | x μ| = − 5 2.24 0.0005 0.1080 0.1075 = − = 2 小 2 大 S S F =
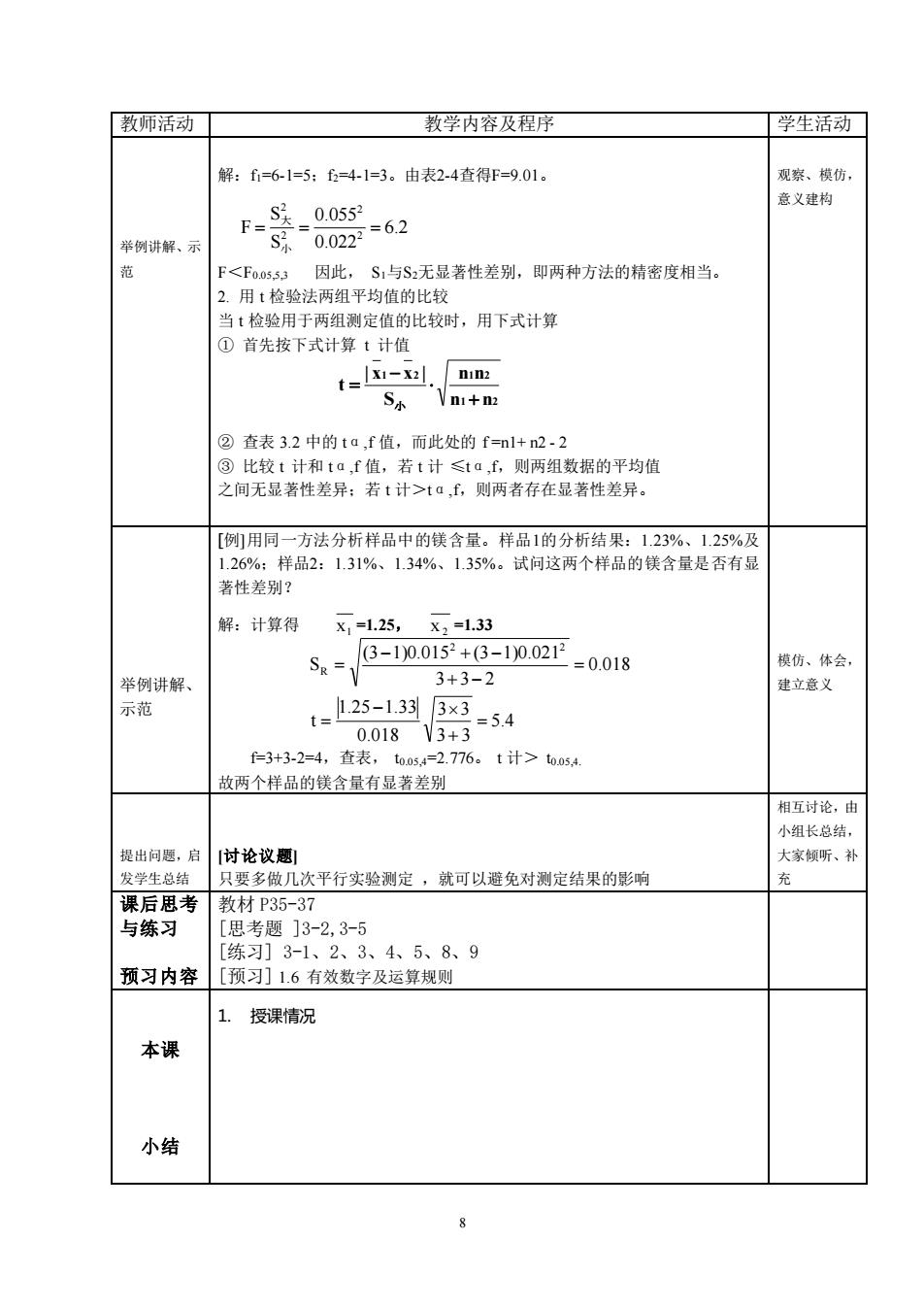
教师活动丁 教学内容及程序 学生活动 解:f=6-1=5:f=4-1=3。由表24查得F=9.01。 观察、模仿 F-S0055 意义建构 举例讲解、示 $家0022=62 因此,S1与S无显著性差别,即两种方法的精密度相当。 2. 平均值的比较 当t检验用于两组测定值的比较时,用下式计算 ①首先按下式计算【计值 t=-, S小 n+m ②查表3.2中的ta,f值,而此处的f=nl+n2-2 ③比较t计和ta,f值,若t计≤ta,f,则两组数据的平均值 之间无显著性差异:若t计>ta,£,则两者存在显著性差异。 [例用同一方法分析样品中的镁含量。样品1的分析结果:123%、 1.25%及 126%:样品2:1.31%、134%、1.35%。试问这两个样品的镁含量是否有显 著性差别? 解:计算得 x,=1.25,x.=1.33 举例讲解、 Se= 3-100.0152+(3-10.0212 =0.018 模仿、体会 3+3-2 建立意义 示范 t=25-13 3x3 0.018V3+3 =5.4 f=3+3-2=4,查表,t0054=2.776。t计>t0o5 两个样品的镁含量有显著差别 相互讨论,由 小组长总结, 提出问题,启【讨论议题 大家倾听、补 发学生点结 只要多做几次平行实验测定,就可以避免对测定结果的影响 里后用老 材p35-37 与练习 题]3-2,3-5 [练习]3-1、2、3、4、5、8、9 预习内容 [预习]1.6有效数字及运算规则 1. 授课情况 本课 小结
8 教师活动 教学内容及程序 学生活动 举例讲解、示 范 解:f1=6-1=5;f2=4-1=3。由表2-4查得F=9.01。 F<F0.05,5,3 因此, S1与S2无显著性差别,即两种方法的精密度相当。 2. 用 t 检验法两组平均值的比较 当 t 检验用于两组测定值的比较时,用下式计算 ① 首先按下式计算 t 计值 ② 查表 3.2 中的 tα,f 值,而此处的 f =n1+ n2 - 2 ③ 比较 t 计和 tα,f 值,若 t 计 ≤tα,f,则两组数据的平均值 之间无显著性差异;若 t 计>tα,f,则两者存在显著性差异。 观察、模仿, 意义建构 举例讲解、 示范 [例]用同一方法分析样品中的镁含量。样品1的分析结果:1.23%、1.25%及 1.26%;样品2:1.31%、1.34%、1.35%。试问这两个样品的镁含量是否有显 著性差别? 解:计算得 1 x =1.25, 2 x =1.33 f=3+3-2=4,查表, t0.05,4=2.776。 t 计> t0.05,4. 故两个样品的镁含量有显著差别 模仿、体会, 建立意义 提出问题,启 发学生总结 [讨论议题] 只要多做几次平行实验测定 ,就可以避免对测定结果的影响 相互讨论,由 小组长总结, 大家倾听、补 充 课后思考 与练习 预习内容 教材 P35-37 [思考题 ]3-2,3-5 [练习] 3-1、2、3、4、5、8、9 [预习] 1.6 有效数字及运算规则 本课 小结 1. 授课情况 6.2 0.022 0.055 S S F 2 2 2 小 2 大 = = = 1 2 1 2 小 1 2 n n n n S | x x | t + − = 5.4 3 3 3 3 0.018 1.25 1.33 t 0.018 3 3 2 (3 1)0.015 (3 1)0.021 S 2 2 R = + − = = + − − + − =

教师活动门 教学内容及程序 学生活动 2. 来自学生的反馈 ◇第2次课 课题 1.6有效数字及运算规则 学时2 教学 1. 掌握误有效数字概念 目标 掌握有效数字及其修约规则、计算规则 了解有效数字在实际测量中的意义 教学 教学有效数字及其修约规 重点有效数字概念及其修约规则、计算规则 难占到 学生已有 先前知识 四则运算,对数运算 知识 前概念 学生持有的对有效数字的误解 主要的教学 程序启发教学 主要教学 方法或策略 辅助手段 基本教材 《分析化学》胡广林、许辉主编中国农业大学出版社 或主要参考书 《分析化学》华中师大等编高等教育出版社 。教学程序表 教师活动 教学内容及程序 学生活动 利用媒体创 感闻问题,明 设情境 创设课堂情境,引起学生的注意,提出本节课要解决的问题 确任各 引发学生回 有效数字(significant figure 忆已有知识佩 在分析工作中实际测量到的数字,除最后一位是可疑的外,其余 复习旧知 的数字都是确定的。 启迪新知 用多媒体品示 感知,体会,建 阐述,强调有效 分析天平称量:12123(g)(万分之一) 立意义 数字由二部分 确定数字可疑数字 组成:确定数宇 可疑数字 滴定管读数:23.26(ml 多体是例。诊 试看下面各数的有效数字的位数 形成“有效数三
9 教师活动 教学内容及程序 学生活动 2. 来自学生的反馈 第 2 次课 课题 1.6 有效数字及运算规则 学时 2 教学 目标 1. 掌握误有效数字概念 2. 掌握有效数字及其修约规则、计算规则 3. 了解有效数字在实际测量中的意义 教学 重点 有效数字概念及其修约规则、计算规则 教学 难点 有效数字及其修约规 则 学生已有 知识 先前知识 四则运算,对数运算 前概念 学生持有的对有效数字的误解 主要的教学 方法或策略 程序启发教学 主要教学 辅助手段 基本教材 或主要参考书 《分析化学》胡广林、许辉主编 中国农业大学出版社 《分析化学》华中师大等编 高等教育出版社 ⚫ 教学程序表 教师活动 教学内容及程序 学生活动 利 用媒 体 创 设情境 创设课堂情境,引起学生的注意,提出本节课要解决的问题 感知问题,明 确任务 1.6 有效数字及运算规则 引发学生回 忆已有知识阐 述 1.6.1 有效数字(significant figure) 1.有效数字(significant figure) 在分析工作中实际测量到的数字,除最后一位是可疑的外,其余 的数字都是确定的。 复习旧知 启迪新知 用多媒体显示 阐 阐述,强调有效 数字由二部分 组成:确定数字 可疑数字 分析天平称量:1.212 3 (g) (万分之一) 确定数字 可疑数字 滴定管读数:23.2 6 (ml) 感知,体会,建 立意义 多媒体显例,诊 试看下面各数的有效数字的位数: 形成“有效数字

「教师活动T 教学内容及程序 学生活动 断学生概念 4.3181 1.00 的位数”有概念 0.1000 10.98% 0.0382 1.98×10-10 005 2×105 260n 100 pH=11.20对应于H+]6.3×10-12 注意 用多媒体显示 (1)数据中的0作具体分析,如1.2007g,0.0012007kg均为五位 有效数值 先判断、偿试错 强调注意 (2)对数运算所得数据,只有尾数为有效数字,首数仅代表原数据的 误,后领会 方次,故不是有效数字 所以,PH值、PM值、等,小数点后的数字才是有效数字。 如pH=10.20,应为两位有效数值 根据有效数字最后一位是如何保留的,可大致判断测定的绝对误差及 用多媒体品示 所用仪器的准确度 分析天平的 数,滴定管的读 绝对误 相对误差 .0.0002 ≈+0.05% 0.4270 体会,练习 先布置练习再 偿试错误,引起 引入新知 2.有效数字的修约规则 认知冲突 [例]将下列数据修约为四位有效数字 0.52664 0.36066 应保留的有效数字位数确定之后,其余尾数 一律舍弃的过程称为修 约。修约应一次到位,不得连续多次修约。 修约规则:四舍六入五成双 观察、模仿,意 当被修约数为5时 义建成构 结合实例讲解 若5后为0,5前为偶数(或0)则舍,5前为奇数则入 10.245010.24 10.2350 10,25 若5后不是0,无论5前是偶或奇皆入 10.13510.14 1.6.2有效数字的运算规则 澄清“小数点后 1.先修约,后计算 位数与绝对误 2数值相加减时,结果保留小数点后位数应与小数点后位数最少者 差”的关系 相同(绝对误差最大) 0.0121+12.56+7.8432=0.01+12.56+7.84=20.41 总绝对误差取决于绝对误差大的 10
10 教师活动 教学内容及程序 学生活动 断学生前概念 4.3181 1.0008 0.1000 10.98% 0.0382 1.98×10-10 0.05 2×105 3600 100 pH=11.20 对应于[H+]=6.3×10-12 的位数”有概念 用多媒体显示 强调注意 注意 (1) 数据中的“0”作具体分析,如 1.2007g, 0.0012007kg 均为五位 有效数值 (2)对数运算所得数据,只有尾数为有效数字,首数仅代表原数据的 方次,故不是有效数字。 所以,PH 值、PM 值、等,小数点后的数字才是有效数字。 如 pH=10.20, 应为两位有效数值 先判断、偿试错 误,后领会 用多媒体显示 分析天平的读 数,滴定管的读 数 根据有效数字最后一位是如何保留的,可大致判断测定的绝对误差及 所用仪器的准确度. 如: 有效数字 0.4272 绝对误差 相对误差 体会,练习 先布置练习再 引入新知 结合实例讲解 2.有效数字的修约规则 [例]将下列数据修约为四位有效数字 0.52664 0.36066 应保留的有效数字位数确定之后,其余尾数一律舍弃的过程称为修 约。修约应一次到位,不得连续多次修约。 修约规则:四舍六入五成双 当被修约数为5时 若5后为0 ,5前为偶数(或0)则舍,5前为奇数则入 10.2450 10.24 10.2350 10.25 若5后不是0 ,无论5前是偶或奇皆入 10.210.135 10.14 偿试错误,引起 认知冲突 观察、模仿,意 义建成构 澄清“小数点后 位数与绝对误 差”的关系 1.6.2 有效数字的运算规则 1. 先修约,后计算 2.数值相加减时,结果保留小数点后位数应 与小数点后位数最少者 相同(绝对误差最大) 0.0121+12.56+7.8432=0.01+12.56+7.84=20.41 总绝对误差取决于绝对误差大的 0.0002 0.05% 0.4270 0.0002