
(1),(2)两式相比,得: ndz +ndz +.+ndzs =0 即 ∑nedZ=0 B=1 这就称为Gibbs-Duhem公式,说明偏摩尔量之间 是具有一定联系的。某一偏摩尔量的变化可从其它 偏摩尔量的变化中求得。 这个公式在多组分系统中很有用。 26 山东理工大学
26 山东理工大学 这就称为Gibbs-Duhem公式,说明偏摩尔量之间 是具有一定联系的。某一偏摩尔量的变化可从其它 偏摩尔量的变化中求得。 (1),(2)两式相比,得: 1 1 2 2 k k d d d 0 n Z n Z n Z + ++ = k B B B=1 即 n Zd = 0 这个公式在多组分系统中很有用

§4.4化学势 1.化学势的定义 在多组分系统中,每个热力学函数的变量就不 止两个,还与组成系统各物的物质的量有关,所 以要在基本公式中增加组成这个变量。 (1)吉布斯自由能 设系统中有1,2,3,.,k个组分 所含的量分别为n1,n2,‘,nk G=G(T,p,n,n2,.,nk) 27 山东理工大学
27 山东理工大学 §4.4 化 学 势 1. 化学势的定义 在多组分系统中,每个热力学函数的变量就不 止两个,还与组成系统各物的物质的量有关,所 以要在基本公式中增加组成这个变量。 (1)吉布斯自由能 设系统中有 1,2,3, ,k 个组分 所含的量分别为 1 2 , , , n n nk 1 2 ( , , , , , ) G G T p n n n = k
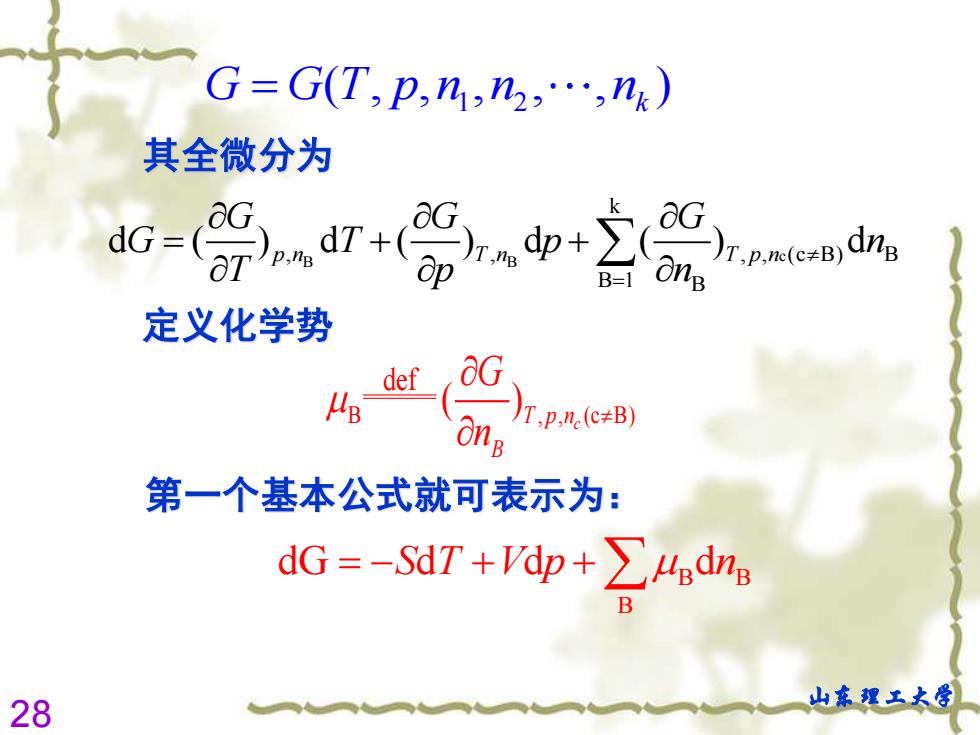
G=G(T,p,n1,n2,.,nk) 其全微分为 定义化学势 def JT,p,e(c≠B) 第一个基本公式就可表示为: dG=-SdT+dp+∑4edn B 28 山东埋王大学
28 山东理工大学 c B B k , , , , (c B) B B 1 B d ( ) d ( ) d ( ) d p n T n T p n G G G G T p n T p n = = + + 其全微分为 定义化学势 B , , (c B) def ( ) c T p n B G n 第一个基本公式就可表示为: B B B dG d d d = − + + S T V p n 1 2 ( , , , , , ) G G T p n n n = k

dH dG+d(TS)=-SdT +Vdp+>ugdng +TdS+SdT =TdS+Vp+∑4gdng 冈无法显示该图片。 相应的化学势定义式为: def S,p,n(c≠B) 同理 。一),y,n.cB) S,',ne(c≠B) 29 山东理工大学
29 山东理工大学 相应的化学势定义式为: B , , (c B) def ( ) c S p n B H n , , (c B) ( )T V nc B A n = , , (c B) ( ) c S V n B U n = dH dG d TS = + ( ) B B B = − + + + + SdT Vdp dn TdS SdT B B B = + + TdS Vdp dn 同理
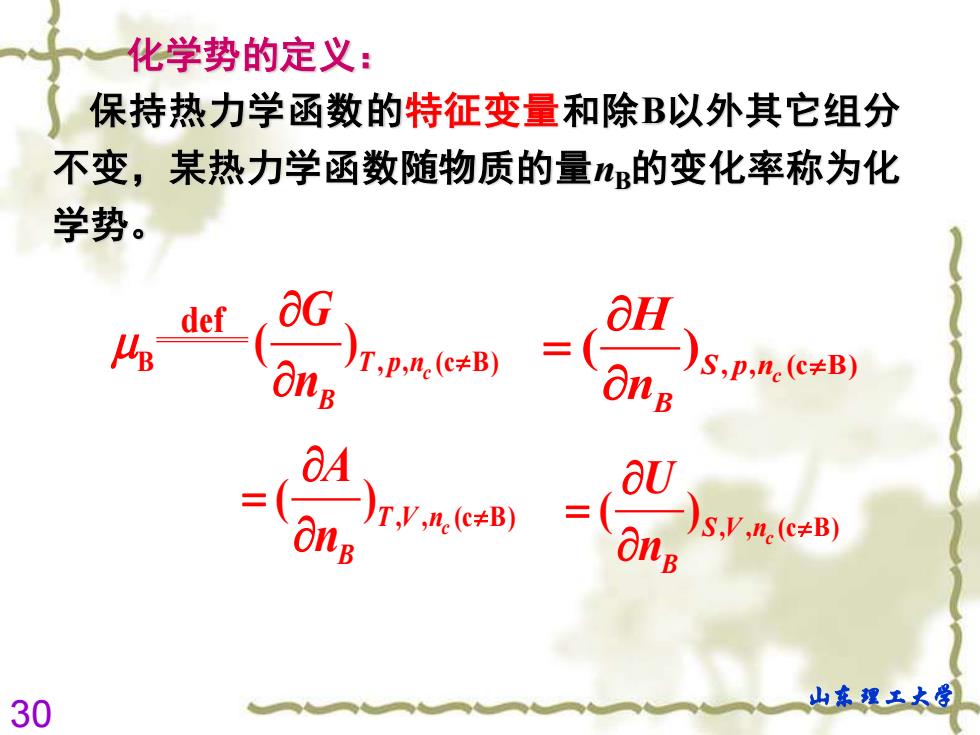
化学势的定义: 保持热力学函数的特征变量和除B以外其它组分 不变,某热力学函数随物质的量的变化率称为化 学势。 def OH 4 OnB T,p.ne(c+B) 01B S,p,ne(c≠B) 6 。)r,y,n.(c#B) aU )5.V,n.(CzB) Ong 30 山东理工大学
30 山东理工大学 化学势的定义: 保持热力学函数的特征变量和除B以外其它组分 不变,某热力学函数随物质的量nB的变化率称为化 学势。 B , , (c B) def ( )T p nc B G n , , (c B) ( )T V nc B A n = , , (c B) ( ) c S V n B U n = , , (c B) ( )S p nc B H n =