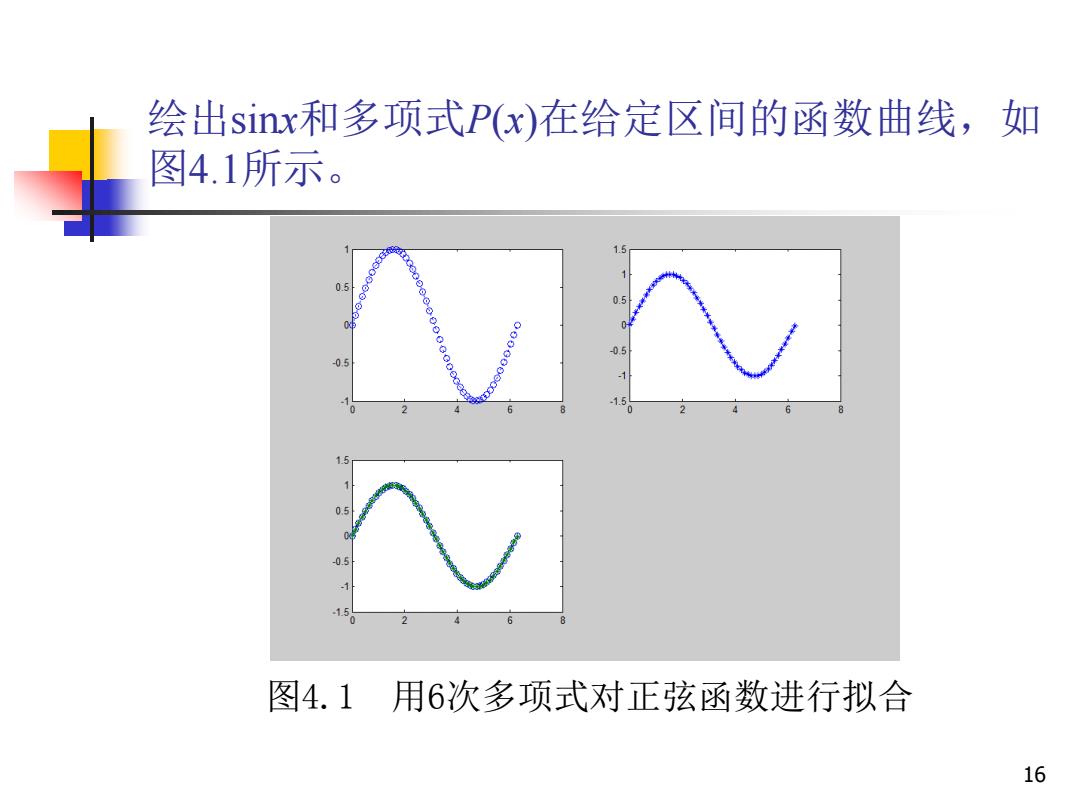
绘出sinx和多项式P(x)在给定区间的函数曲线,如 图4.1所示。 05 ⊙ 0.5 0.5 6 图4.1用6次多项式对正弦函数进行拟合 16
16 绘出sinx和多项式P(x)在给定区间的函数曲线,如 图4.1所示。 图4.1 用6次多项式对正弦函数进行拟合

4.数据插值 插值运算(插值法):又称内插法。根据未知函数 f(x)在某区间内若干点的函数值,作出在该若干点 的函数值与f(x)值相等的特定函数来近似原函数 f(x),进而可用此特定函数算出该区间内其他各点 的原函数f(x)的近似值,这种方法,称为内插法。 ■ 按特定函数的性质分,有线性内插、非线性内插等; 按引数(自变量)个数分,有单内插、双内插和三内 插等。 17
17 4.数据插值 插值运算(插值法):又称内插法。根据未知函数 f(x)在某区间内若干点的函数值,作出在该若干点 的函数值与f(x)值相等的特定函数来近似原函数 f(x),进而可用此特定函数算出该区间内其他各点 的原函数f(x)的近似值,这种方法,称为内插法。 按特定函数的性质分,有线性内插、非线性内插等; 按引数(自变量)个数分,有单内插、双内插和三内 插等

(1)一维数据插值 在MATLAB中,实现一维数据插值的函数是interpl,被 插值函数是一个单变量函数,其调用格式为 yi=interpl(x,y,xi,method) 函数根据x,y的值,计算函数在xi处的函数值。x,y是两 个等长的已知向量,分别描述采样点和样本值。 xi是一个向量或标量,描述欲插值的点,yi是一个与xi 等长的插值结果。 method是插值方法,允许的取值有'linear'、'nearest'、 'cubic''、'spline',分别表示线性插值、最近点插值、3次 多项式插值、3次样条插值。 注意:x的取值范围不能超出x的给定范围,否则,会 给出“NaN”错误。 18
18 (1) 一维数据插值 在MATLAB中,实现一维数据插值的函数是interp1,被 插值函数是一个单变量函数,其调用格式为 yi=interp1(x, y, xi, method) 函数根据x, y的值,计算函数在xi处的函数值。x, y是两 个等长的已知向量,分别描述采样点和样本值。 xi是一个向量或标量,描述欲插值的点,yi是一个与xi 等长的插值结果。 method是插值方法,允许的取值有'linear'、'nearest'、 'cubic'、'spline',分别表示线性插值、最近点插值、3次 多项式插值、3次样条插值。 注意:xi的取值范围不能超出x的给定范围,否则,会 给出“NaN”错误

例4.4向量t和p表示从1900~1990年的每隔10年 的美国人口普查数据: ■1 =1900:10:1990; ■p=[75.99591.972105.711123.203131.669. ■ 150.697179.323203.212226.505249.633]; 根据人口普查数据估计1975年的人口,并利用插 值估计从1900~2000年每年的人口数。 19
19 例4.4 向量t和p表示从1900~1990年的每隔10年 的美国人口普查数据: t=1900:10:1990; p=[75.995 91.972 105.711 123.203 131.669... 150.697 179.323 203.212 226.505 249.633]; 根据人口普查数据估计1975年的人口,并利用插 值估计从1900~2000年每年的人口数

首先在命令窗口输入插值命令interpl(t,p,1975),估计 1975年的人口,返回结果如下: ans= 214.8585 再利用插值估计1900~2000年每年的人口数,并利用 画图命令得出曲线分布。程序如下: ■x=1900:1:2000: y=interpl(t,p,x,'spline');%样条插值 plot(t,p,':o',x,y,'-r') ■%带圆圈标记的虚线(:0)为普查数据,红实线(-)为插值数据 所得曲线如图4.2所示。 20
20 首先在命令窗口输入插值命令interp1(t, p, 1975),估计 1975年的人口,返回结果如下: ans= 214.8585 再利用插值估计1900~2000年每年的人口数,并利用 画图命令得出曲线分布。程序如下: x=1900:1:2000; y=interp1(t, p, x, 'spline'); %样条插值 plot(t, p, ':o', x, y, '-r') %带圆圈标记的虚线(:o)为普查数据,红实线(-r)为插值数据 所得曲线如图4.2所示