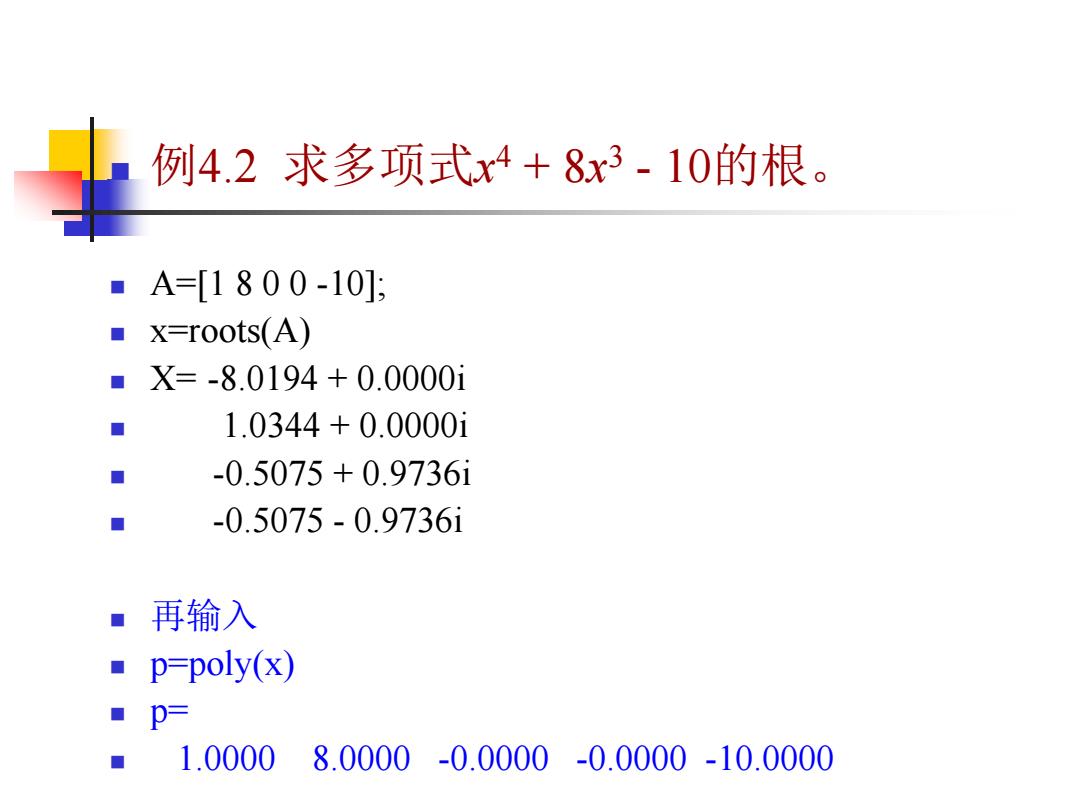
例4.2求多项式x4+8x3-10的根。 ■A=[1800-10]; ■】 x=roots(A) ■X=-8.0194+0.0000i ■ 1.0344+0.0000i ■ -0.5075+0.9736i ■ -0.5075-0.9736i ■ 再输入 ■】 p=poly(x) ■p= 1.0000 8.0000 -0.0000-0.0000-10.0000
例4.2 求多项式x 4 + 8x 3 - 10的根。 A=[1 8 0 0 -10]; x=roots(A) X= -8.0194 + 0.0000i 1.0344 + 0.0000i -0.5075 + 0.9736i -0.5075 - 0.9736i 再输入 p=poly(x) p= 1.0000 8.0000 -0.0000 -0.0000 -10.0000

3.曲线拟合 曲线拟合:目的是用一个较简单的函数去逼近一个 复杂的或未知的函数,即从一系列已知离散点上的 数据集[(x1,y1),(x2,y2),·,(区n,y)]上得到一个解 析函数y=f(x),得到的解析函数f(x)应当在原离散 点x1上尽可能接近给定的y;值。 常用拟合的方法有:最小二乘法,拉格朗日插值法、牛顿插 值法、牛顿迭代法、区间二分法、弦截法、 雅克比迭代法和 牛顿科特斯数值积分法等方法。 12
12 3.曲线拟合 曲线拟合:目的是用一个较简单的函数去逼近一个 复杂的或未知的函数,即从一系列已知离散点上的 数据集[(x1,y1),(x2,y2),…,(xn,yn)]上得到一个解 析函数y=f(x),得到的解析函数f(x)应当在原离散 点xi上尽可能接近给定的yi值。 常用拟合的方法有:最小二乘法,拉格朗日插值法、牛顿插 值法、牛顿迭代法、区间二分法、弦截法、雅克比迭代法和 牛顿科特斯数值积分法等方法

3.曲线拟合 在MATLAB中用polyfiti函数来求得最小二乘拟合 多项式的系数,再用polyvali函数按所得的多项式 计算所给出的点上的函数近似值。 ■polyfitp函数的调用格式为 ■P,S]=polyfit(X,Y,m) 函数根据采样点X和采样点函数值Y,产生一个m 次多项式P及其在采样点的误差向量S。其中X,Y 是两个等长的向量,P是一个长度为m+1的向量, P的元素为多项式系数。 13
13 3.曲线拟合 在MATLAB中用polyfit函数来求得最小二乘拟合 多项式的系数,再用polyval函数按所得的多项式 计算所给出的点上的函数近似值。 polyfit函数的调用格式为 [P, S]=polyfit(X, Y, m) 函数根据采样点X和采样点函数值Y,产生一个m 次多项式P及其在采样点的误差向量S。其中X, Y 是两个等长的向量,P是一个长度为m + 1的向量, P的元素为多项式系数
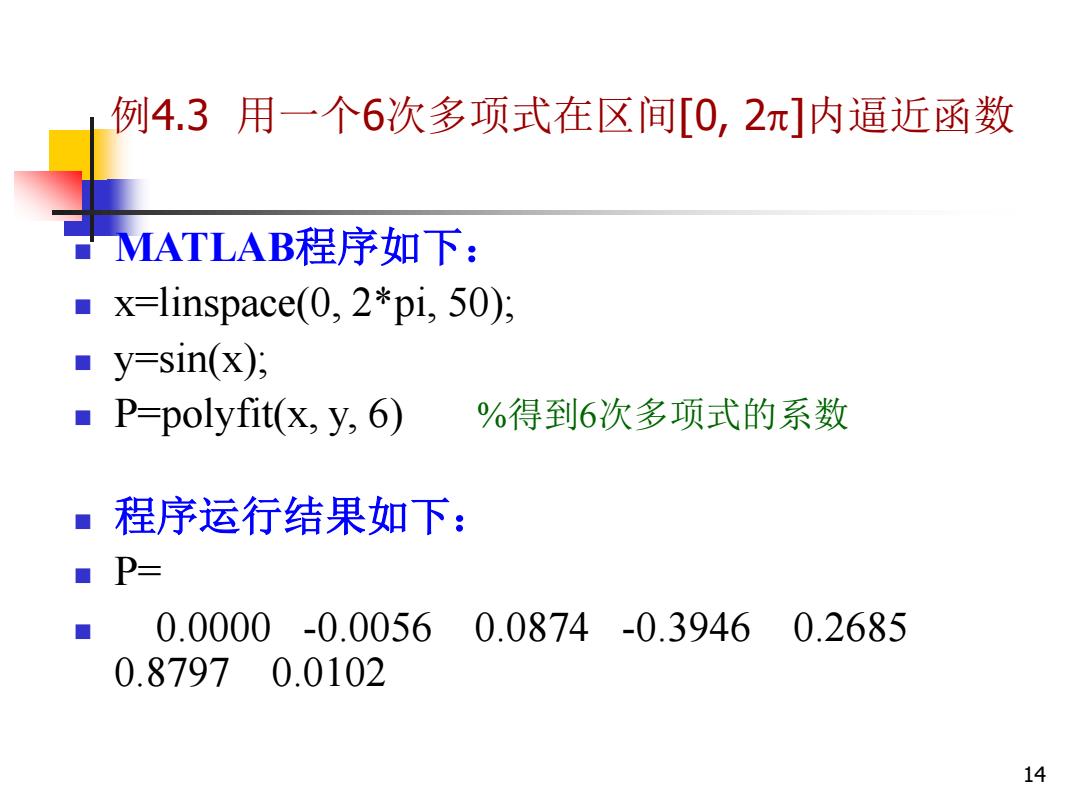
例4.3用一个6次多项式在区间[0,2π]内逼近函数 MATLAB程序如下: x=linspace(0,2*pi,50); ■y=sin(x); ■P=polyfit(x,y,6) %得到6次多项式的系数 程序运行结果如下: ■P= 0.0000-0.0056 0.0874-0.3946 0.2685 0.87970.0102 14
14 例4.3 用一个6次多项式在区间[0, 2]内逼近函数 MATLAB程序如下: x=linspace(0, 2*pi, 50); y=sin(x); P=polyfit(x, y, 6) %得到6次多项式的系数 程序运行结果如下: P= 0.0000 -0.0056 0.0874 -0.3946 0.2685 0.8797 0.0102

利用绘图方法将多项式P(x)和sinx进行比较 x=linspace(0,2*pi,50); ■y=sin(x); ■f=polyval(P,x); subplot(2,2,1),plot(x,y,:o); subplot(2,2,2),plot(x,f,'-*); subplot(2,2,3),plot(x,y,':o',x,f,'-*); 15
15 利用绘图方法将多项式P(x)和sinx进行比较 x=linspace(0, 2*pi, 50); y=sin(x); f=polyval(P,x); subplot(2,2,1),plot(x,y,':o'); subplot(2,2,2), plot(x,f,'-*'); subplot(2,2,3), plot(x,y,':o',x,f,'-*');