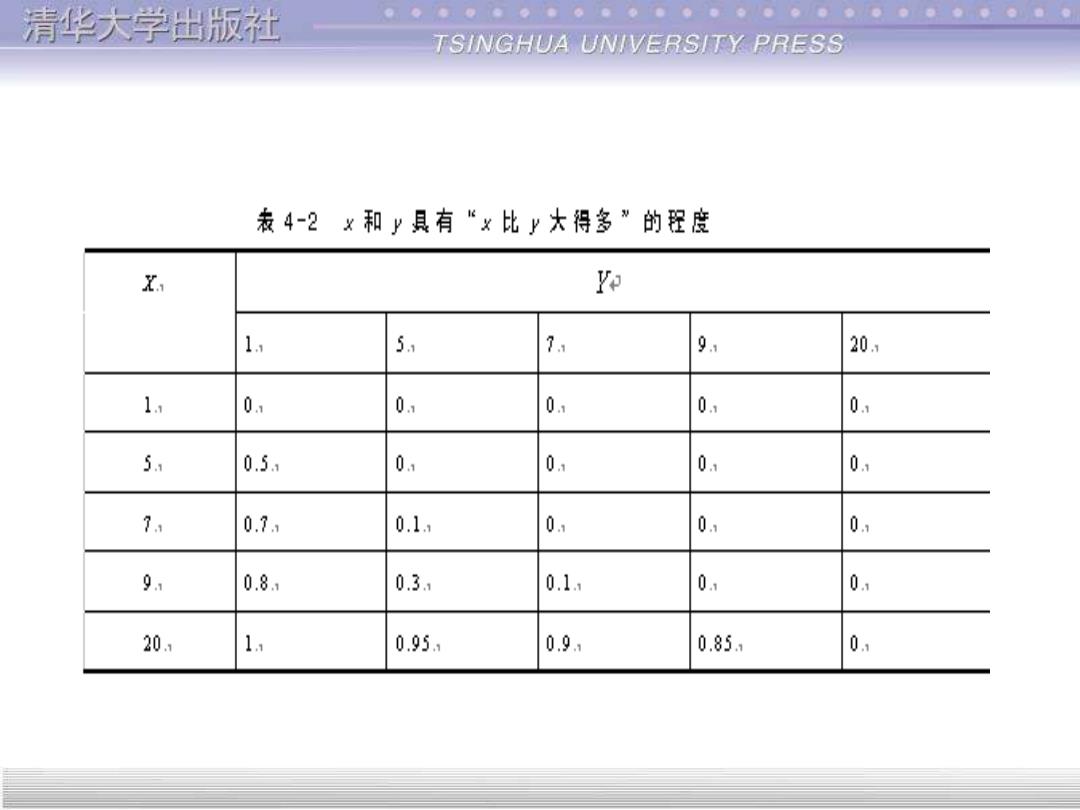
清华大学出版社 TSINGHUA UNIVERSITY PRESS 表4-2x和y具有“x比y大得多”的程度 X Ve 1 5 71 91 20. 1 0. 0 0 0 0 5 0.5 01 0 0 0 7 0.7 0.1 0 01 0 91 0.8 0.3 0.1 01 01 20 1 0.95 0.9 0.85. 0

清华大学出版社 TSINGHUA UNIVERSITY PRESS 相应的模糊矩阵为: [0 0 0 0 0 0.5 0 0 0 0 = 0.7 0.1 0 0 0 0.8 0.3 0.1 0 0 1 0.95 0.9 0.85
相应的模糊矩阵为 : R= 1 0.95 0.9 0.85 0 0.8 0.3 0.1 0 0 0.7 0.1 0 0 0 0.5 0 0 0 0 0 0 0 0 0

清华大学出版社 TSINGHUA UNIVERSITY PRESS 模糊关系的自返性、对称性、传递性。 ①自返性。.一个模糊关系R,若x∈X,有4.(x,x)=1, 即每一个元素x与自身隶属于模糊关系的程度为1,则称R 为具有自返性的模糊关系。例如,相像关系就具有自返性, 仇敌关系不具有自返性。 ② 对称性。一个模糊关系R,、若xy∈X,均有4(x,D H(),即x与隶属宇模糊关系的程度和与隶属 手模糊矢系的叠属繁养養看鹦琴塞的復暴 例如,相像关系就具有对称性,而相爱关系就不具有对称 性 ③传递性。一个模糊关系R,若x,y,z∈X,均有4(x, z,≥minμ(,以,4RGy,z)门, 即x与y隶属于模糊关系 R的程度和y与隶属于模糊关系R的程度中较小的一个值 郡小于x与隶属于模糊关系R的程度,则称R为具有传递 性的模糊关系
模糊关系的自返性、对称性、传递性。 • ① 自返性。一个模糊关系R,若x∈X,有μR (x,x)=1, 即每一个元素x与自身隶属于模糊关系R的程度为1,则称R 为具有自返性的模糊关系。例如,相像关系就具有自返性, 仇敌关系不具有自返性。 • ② 对称性。一个模糊关系R,若x,y∈X,均有μR (x,y) =μR (y,x),即x与y隶属于模糊关系R的程度和y与x隶属 于模糊关系R的程度相同,则称R为具有对称性的模糊关系。 例如,相像关系就具有对称性,而相爱关系就不具有对称 性。 • ③ 传递性。一个模糊关系R,若x,y,z∈X,均有μR (x, z) ≥min[μR (x,y),μR (y,z)],即x与y隶属于模糊关系 R的程度和y与z隶属于模糊关系R的程度中较小的一个值 都小于x与z隶属于模糊关系R的程度,则称R为具有传递 性的模糊关系

清华大学出版社 TSINGHUA UNIVERSITY PRESS 3.模糊矩阵 当={xi=1,2,,m,{y广1,2,,n}是有限集合 时,则×的模糊关系阿用下列mX阶矩阵来表示: r r21 22 n R- (4-4) i ri Ym2 其中:元素=”里(xy)。该矩阵被称为模糊矩阵, 简记为: R=[rijnxn
3. 模糊矩阵 当X={xi |i=1,2, …,m}, Y={yj |j=1,2, …,n}是有限集合 时,则X×Y的模糊关系R可用下列m×n阶矩阵来表示: R= (4-4) 其中: 元素rij =μR (xi,yj )。该矩阵被称为模糊矩阵, 简记为: R=[rij ]m×n m m mj mn i i i j i n j n j n r r r r r r r r r r r r r r r r 1 2 1 2 21 22 2 2 11 12 1 1

清华大学出版社 TSINGHUA UNIVERSITY PRESS ·为讨论模糊矩阵运算方便,设矩阵为m×阶方阵,即R= [rxn'里=[gxn'此时模糊矩阵的交、并、补运算 为: (1)模糊矩阵交 Rn=[r∧qmxa (4-5) (2)模糊矩阵并 RUQ=[rij aijnxn (4-6) (3)模糊矩阵补 =[1一rmxn (4-7)
• 为讨论模糊矩阵运算方便,设矩阵为m×n阶方阵,即R= [r ij ]m×n,Q=[qij ]m×n,此时模糊矩阵的交、并、补运算 为: ⑴ 模糊矩阵交 R∩Q=[rij∧qij ]m×n (4-5) ⑵ 模糊矩阵并 R∪Q=[rij∨qij ]m×n (4-6) ⑶ 模糊矩阵补 Rc=[1-rij] m×n (4-7)