
清华大学出版社 TSINGHUA UNIVERSITY PRESS 4.1模糊逻辑的数学基础 4.1.1 模糊集合 4.1.2 模糊集合的表示方法 4.1.3模糊集合的运算 4.1.4隶属函数确定方法 4.1.5模糊关系 可
4.1 模糊逻辑的数学基础 4.1.1 模糊集合 4.1.2 模糊集合的表示方法 4.1.3 模糊集合的运算 4.1.4 隶属函数确定方法 4.1.5 模糊关系

清华大学出版社 TSINGHUA UNIVERSITY PRESS 4.1.1 模糊集合 ·在人类的思维中,有许多模糊的概念,如大、小、冷、 热等,都没有明确的内涵和外延,只能用模糊集合来描述; 有的概念具有清晰的内涵和外延,如男人和女人。我们把 前者叫做模糊集合,用大写字母下添加波浪线表示,如4 表示模糊集合,而后者叫做普通集合(或经典集合)。 一般而言,在不同程度上具有某种特定属性的所有元素 的总合叫做模糊集合。 ·例如,胖子就是一个模糊集合,它是指不同程度发胖的 那群人,它没有明确的界线,也就是说你无法绝对地指出 哪些人属于这个集合,而哪些人不属于这个集合,类似这 样的概念,在人们的日常生活中随处可见
4.1.1 模糊集合 • 在人类的思维中,有许多模糊的概念,如大、小、冷、 热等,都没有明确的内涵和外延,只能用模糊集合来描述; 有的概念具有清晰的内涵和外延,如男人和女人。我们把 前者叫做模糊集合,用大写字母下添加波浪线表示,如A 表示模糊集合,而后者叫做普通集合(或经典集合)。 • 一般而言,在不同程度上具有某种特定属性的所有元素 的总合叫做模糊集合。 • 例如,胖子就是一个模糊集合,它是指不同程度发胖的 那群人,它没有明确的界线,也就是说你无法绝对地指出 哪些人属于这个集合,而哪些人不属于这个集合,类似这 样的概念,在人们的日常生活中随处可见

清华大学出版社 TSINGHUA UNIVERSITY PRESS 隶属函数 在普通集合中,曾用特征函数来描述集合,而对于模 糊性的事物,用特征函数来表示其属性是不恰当的。因为 模糊事物根本无法断然确定其归属。为了能说明具有模糊 性事物的归属,可以把特征函数取值0、1的情况,改为对 闭区间[0,1]的取值。这样,特征函数就可取0~1之间的 无穷多个值,即特征函数演变成可以无穷取值的连续逻辑 函数。从而得到了描述模糊集合的特征函数一一隶属函数, 它是模糊数学中最基本和最重要的概念,其定义为: 用于描述模糊集合,并在[0,1]闭区间连续取值的特征函 数叫隶属函数,隶属函数用4(x)表示,其中表示模糊 集合,而x是的元素,隶属函数满足: 0≤u4(x)≤1
隶属函数 在普通集合中,曾用特征函数来描述集合,而对于模 糊性的事物,用特征函数来表示其属性是不恰当的。因为 模糊事物根本无法断然确定其归属。为了能说明具有模糊 性事物的归属,可以把特征函数取值0、1的情况,改为对 闭区间[0,1]的取值。这样,特征函数就可取0~1之间的 无穷多个值,即特征函数演变成可以无穷取值的连续逻辑 函数。从而得到了描述模糊集合的特征函数——隶属函数, 它是模糊数学中最基本和最重要的概念,其定义为: 用于描述模糊集合,并在[0,1]闭区间连续取值的特征函 数叫隶属函数,隶属函数用μA (x)表示,其中A表示模糊 集合,而x是A的元素,隶属函数满足: 0≤μA (x)≤1

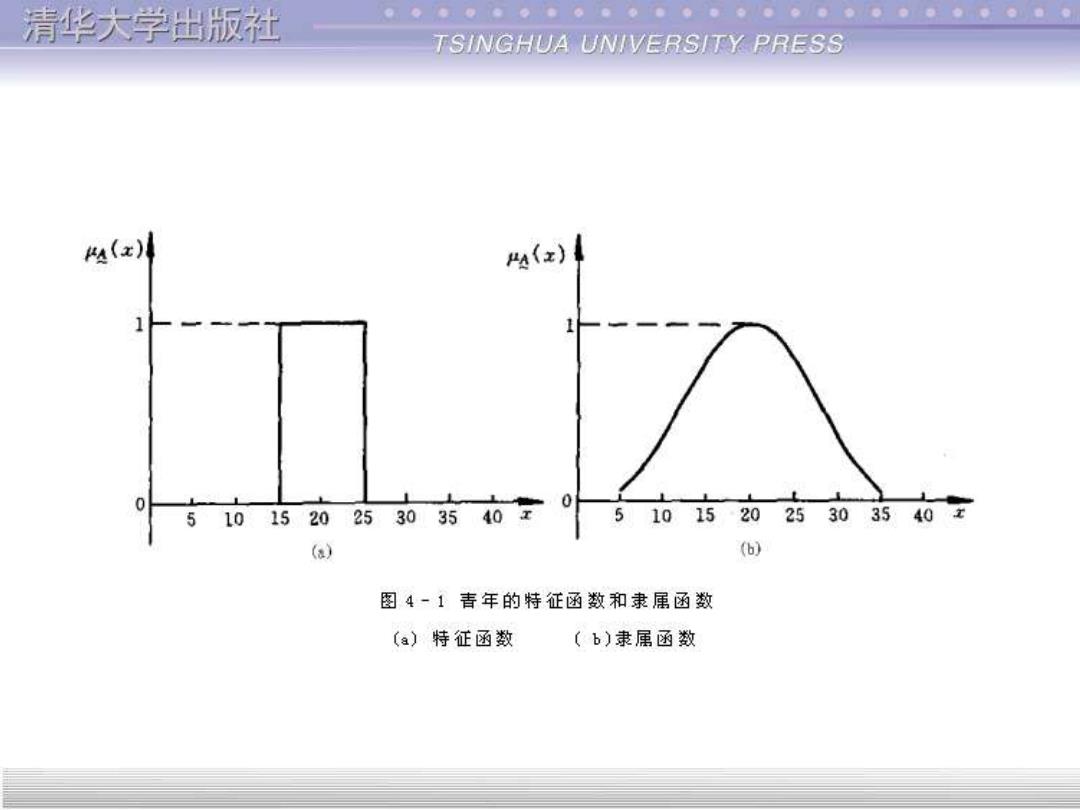
清华大学出版社 TSINGHUA UNIVERSITY PRESS 表示青年的集合 有了隶属函数以后,人们就可以把元素对模 糊集合的归属程度恰当地表示出来。例如青年是 一个集合,用普通集合表示时为集合A,并且有 A={x15岁≤x≤25岁} 则这时的特征函数如图4-1(a)所示。如果用模糊 集合表示,并且有 业4(x)=e9 则这时的隶属函数如图4-1(b)所示
表示青年的集合 有了隶属函数以后,人们就可以把元素对模 糊集合的归属程度恰当地表示出来。例如青年是 一个集合,用普通集合表示时为集合A,并且有 A={x|15岁≤x≤25岁} 则这时的特征函数如图4–1(a)所示。如果用模糊 集合A表示,并且有 μA (x)=e 则这时的隶属函数如图4–1(b)所示。 2 ) 7 20 ( − − x
清华大学出版社 TSINGHUA UNIVERSITY PRESS (x) ma()1 0 510152025303540x 510152025303540五 (a) (6) 图4-1春年的特征函数和隶属函数 (a)特征函数 (b)隶属函数