
绪论 自古以来河流两岸就是人类主要繁衍生总之地。为了发展生产和改善生存环境,人类不 断地与江河作斗争。在长期的斗争中,逐渐掌握了关于河流运动发展的基本规律和河道整治 工程技术的系统知识,其中前者就属于河流动力学的范畴。 河流是水流与河床在地球物理诸自然因素及人类活动的影响下相互作用的产物。水流作 用于河床,使河床发生变化:同时河床也作用于水流,影响水流的特性。二者构成一个矛盾 的统一体,相互依存,相互影响,相互制约,永远处于变化和发展的过程中。 河流有着自身的发展变化规律。人类的许多活动都围绕着河流进行,如修建跨河的桥梁、 防洪的堤坝、过江的隧道、航运的码头、灌溉发电的综合水利枢纽、火电厂的取水口、城市 用水及排水等等,这些活动或多或少地干涉了河流的自然进程,有些则极大地改变了河流的 自然条件。如何认识河流的自身发展变化规律并利用其为人类服务,或者引导其朝着有利于 人类的方向发展,或者最大限度地降低因改变河流自然进程所带来的负面效应,这是河流动 力学学科的根本所在。 我国河流众多,洪水灾害严重。如1998年长江及松花江的全流域性洪水,给国民经济 人民的生命财产安全造成了巨大损失。为了防洪而修建的堤防及护岸工程,一方面保护了两 岸的安全:另一方面,限制了洪水泛滥而直接遭受水流的作用。如果工程的附近的河道稳定, 并且有比较稳定的成型堆积体,则堤防及护岸工程较稳定:如果河道处于冲刷状态,堤防及 护岸工程的安全就会受到威胁。由于河道的冲淤变化,造成主流的位置不断迁徒,不仅给防 洪带来不利,而且可能造成取水口“脱溜”、码头淤废。在河道上修建大型水利枢纽,固然 具有防洪、发电、航运、灌溉等综合效益,但同时也引发了新的问题:如库区回水末端的淤 积及上延,会扩大沌没、浸没面积,抬高地下水位,影响通航:在枢纽的下游,由于上游来 沙被拦蓄在水库里,清水下淮,下游的河床就会发生长距离的冲刷,致使堤岸坍塌:同时由 于流量过程的改变,造成主流位置改变,给下游河道两岸的工程带来不利影响, 河道中的水流是一种挟带有泥沙颗粒的水流,许多情况下河床上也存在着大量的泥沙颗 粒,因此在水流与河床交互作用的过程中,泥沙的运动起着纽带的作用。换句话说,水流和 河床交互作用的过程与结果,要通过泥沙的运动来实现。例如,河床的淤积拾升,就是在 定的条件下通过水流中挟带的泥沙运动实现:河床的冲刷下降,也是在一定的条件下通过河 床上泥沙的起动,由水流挟带输移来实现。事实上,泥沙有时可能是河床的组成部分,有时 又可能是水流的组成部分,当它从矛盾的一个方面转化到中一方面时,河床将发生变化,河 道发生演变。泥沙运动在水流与河床交互作用的这种纽带作用,使得泥沙运动的基本规律的 研究成为河流动力学中的核心问题。 因此,在河流动力学的内容中,泥沙运动的基本规律和河道演变基本规律是核心。而泥 沙运动的基本规律首先涉及到河道水流的运动特性,因此在编写教材时,对河道水流运动的

一些内容加以简要介绍此外为了了解水利水电工程中的泥沙问题及防治措施,增加了工程 泥沙的内容。 泥沙运动是固液两相流,它不同于一般的水流运动,特别是泥沙运动具有很大的随机性 和偶然性。影响泥沙运动和河床演变的因素众多,河道整治的边界条件又非常复杂,在许多 问题上人们的认识还停留在感性和经验阶段上:同时,在泥沙运动、河床演变量测手段上的 许多实际困难,给这一学科的研究发展带来不少困难。因此,这一领域还充满着问题和挑战。 目前,对一些现象的认识尚不统一,一种工程计算往往有多种不同的计算公式,有些问题的 解决甚至无一定的成规可循。这就要求我们学习这门学科时要树立以下基本观点:(1)理论 联系实际,要善于在实践中收集大量资料,通过深入分析,进行理论概括,并能用这些理论 指导治河工程实践,解决工程中的泥沙问题:(2)用运用辩证唯物主义的观点和方法,善于 区别主要矛盾和次要矛盾,在众多复杂的影响因素中,对具体问题找出其主要的影响因素, 简化解决问题的方法和途径。(3)对已经建立的泥沙运动、河床演变及河道整治的经验公式。 要注意公式的来源、建立的条件、最纲和使用范围,不可盲目照抄运用
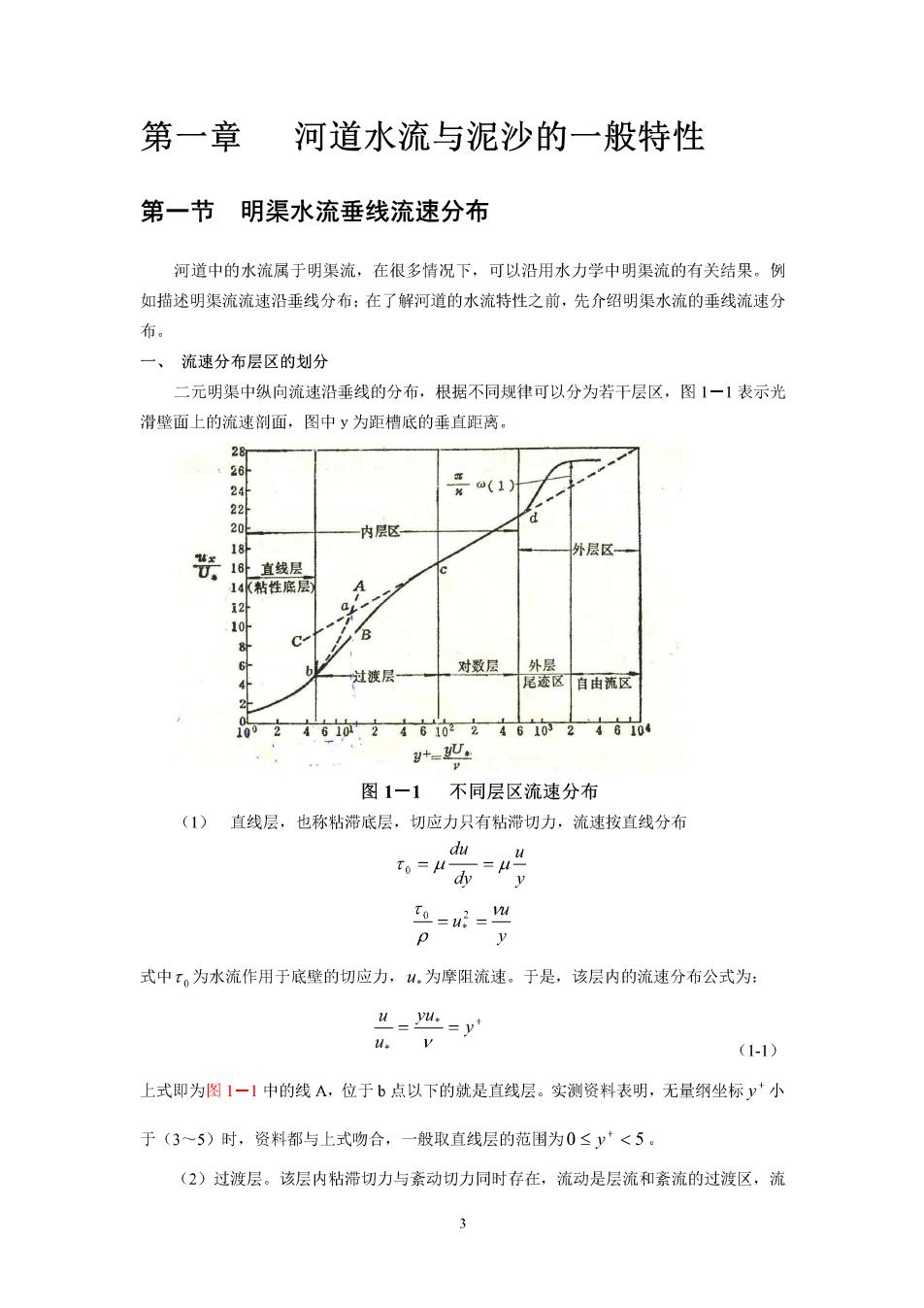
第一章河道水流与泥沙的一般特性 第一节明渠水流垂线流速分布 河道中的水流属于明渠流,在很多情况下,可以沿用水力学中明渠流的有关结果。例 如描述明渠流流速沿垂线分布:在了解河道的水流特性之前,先介绍明渠水流的垂线流速分 布。 一、流速分布层区的划分 二元明渠中纵向流速沿垂线的分布,根据不同规律可以分为若干层区,图1一1表示光 滑壁面上的流速剖面,图中y为距槽底的垂直距离。 花(1 一内层区 层区 16卧直线层 B 过波层一 对数层 外是区自由区 +- 图1一1不同层区流速分布 (1)直线层,也称粘滞底层,切应力只有粘滞切力,流速按直线分布 哈吗 == p y 式中t,为水流作用于底壁的切应力,山,为摩阻流速。于是,该层内的流速分布公式为: 4=以=y u.V (1-1) 上式即为图1一1中的线A,位于b点以下的就是直线层。实测资料表明,无量纲坐标y*小 于(3~5)时,资料都与上式吻合,一般取直线层的范围为0≤y'<5 (2)过波层。该层内粘滞切力与紊动切力同时存在,流动是层流和紊流的过渡区,流 3

速分布如图中的B线(试验曲线),位于bc之间,上部与对数区连接,交于点,该点位 置随边壁情况变化于y*≈30-50,亦可达到y=70。该层区没有统一流速分布公式,近 似按直线层或对数层公式计算。 若将式(1-1)的线A延长与对数层的线C相交于:点,该点位于过波层内,其位置 y'≈11.6,相当于粘滞底层名义厚度6。 (3)对数层。在该层区内,切应力主要为素动切应力,流速按对数曲线分布,如图中直 线C(对数坐标),位于cd段。该层上界d点)位于y≈0.26。6,为边界层厚度,在明渠 或河道中.边界层都己发展到水面,。等于水深 (4)外层区。在对数层以上到水面的区间,即0.26。<y≤6。或(y>500),该层区内 切力主要为紊动切力,流速分布常以缺速公式表示,故也称缺速区。有时将该区又分为外层 尾迹区和自由流区。外层区流速分布要受到上部边界的影响,与壁糙也有一定的关系。 二、对数层流速分布公式 根据图和试验证实,对数层流速分布是./U和粗糙高度k,的函数。由于粗髓高可能 位于直线层内、或突入过渡层内、或突入对数层内等三种情况,因此首先将壁面按粗糙程度 分为三种。 (1)光滑壁面。由实验资料得到 uk<5,或k,<046 式中6-11.6014.为粘滞底层名义厚度。此时,粗糙高受直线层掩盖,对数流速分布只是 w./的函数。 (2)过渡壁面。由实验得到 5<4,k<70或0,46<k,<66 此时,粗糙高伸入过渡层内,对数流速分布既受./心的影响,又受k,的影响。 (3)粗糙壁面。根据实验得到 ,k>70或k,>66 D 下面分析对数层区的流速分布公式。在该层内,水流的切应力主要是奈动切应力,采用普兰 特切应力公式,省略式中的时均符号,即

=pl( (1-2) 在壁面附近,假设x=t。,混合长I=,代入上式得 积分得 w=么ny+c (1-3) 该式就是普兰特对数流速分布式,也就是上述的对数层流速分布公式,式中:是积分常数。 该式虽是根据壁面附近条件得到的,当用实测对数层的流速分布来确定常数值,就可用于整 个对数层。 将式改写为 兰-203gg-203s号+号 多 =Algy'+B (1-4) 4, 式.4=230x,B=-20e告+品 A和B则根据壁面情况通过试验确定。 此外,也可以设yy时0为边界条件代入式(13),得到流速分布公式 (1-5) K yo 坎利根(GH.Keulegan)根据巴青(H.E.Ba7im)的试验资料得到光滑床面A=5,75,B=5.5。 粗糙床面A=5.75,B=8.5. 爱因斯坦(H.A.Einstein)将其合成统一的流速分布公式,适用于各种类型的床面情况 -575g802 (1-6) 式中x为修正系数,它是k,/6的函数,见图1一2