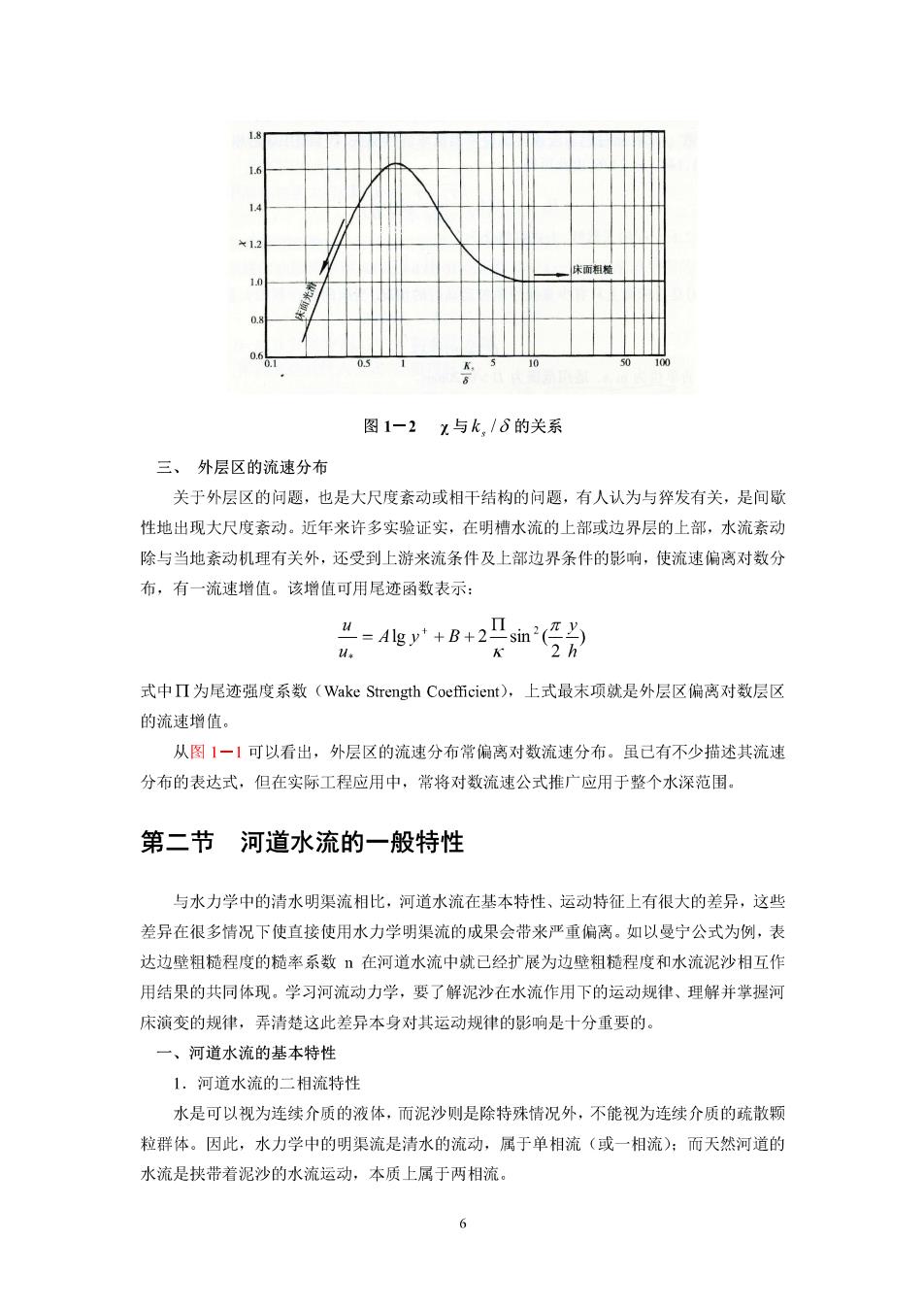
图1-21与k,/8的关系 三、外层区的流速分布 关于外层区的问题,也是大尺度紊动或相干结构的问题,有人认为与猝发有关,是间歇 性地出现大尺度素动。近年来许多实验证实,在明槽水流的上部或边界层的上部,水流素动 除与当地紊动机理有关外,还受到上游米流条件及上部边界条件的影响,使流速偏离对数分 布,有一流速增值。该增值可用尾迹函数表示: -您y+B+2m为 u. 式中Ⅱ为尾迹强度系数(Wake Strength Coefficient),上式最未项就是外层区偏离对数层区 的流速增值。 从图1一1可以看出,外层区的流速分布常偏离对数流速分布。虽己有不少描述其流速 分布的表达式,但在实际工程应用中,常将对数流速公式推广应用于整个水深范用。 第二节河道水流的一般特性 与水力学中的清水明渠流相比,河道水流在基本特性、运动特征上有很大的差异,这些 差异在很多情况下使直接使用水力学明渠流的成果会带来严重偏离。如以曼宁公式为例,表 达边壁粗糙程度的糙率系数在河道水流中就已经扩展为边壁粗糙程度和水流泥沙相互作 用结果的共同体现。学习河流动力学,要了解泥沙在水流作用下的运动规律、理解并学握河 床演变的规律,弄清楚这此差异本身对其运动规律的影响是十分重要的。 一、河道水流的基本特性 1.河道水流的二相流特性 水是可以视为连续介质的液体,而泥沙则是除特殊情况外,不能视为连续介质的疏散颗 粒群体。因此,水力学中的明渠流是清水的流动,属于单相流(或一相流):而天然河道的 水流是扶带者泥沙的水流运动,本质上属于两相流

2.河道水流的三维性 河道水流的过水断面一般是不规则的,不规则的程度,以山区河流为最大,冲积平原中 的顺直河段为最小。因此河道水流为三维流动。 河道水流的三维性与过水断面的宽深比往往互相关联,宽深比愈小,三维性愈强烈。在 顺直的、滩槽比较明显的广阔滩面上,水流的宽深比较大,可能呈现出一定程度的二维性: 而在深谷高峡、宽深比很小的山区河段中,水流的三维性极强。 3.河道水流的不恒定性 水力学中一般明渠流中也有不恒定流,但与河道水流的不恒定性相比,情形要简单得多。 河道水流的不恒定性主要表现在两个方面:一是来水来沙情况随时空的变化,这与水力学相 同:二是由于河床经常处于演变之中,因此河道水流的边界也随时空变化。 我国绝大多数河流的水沙来量和沙质,主要受制于降水。而降水在时空分布上变化非常 大。因此,不同河流的水、沙时空变化也相当大。北方地区的河流变化的相对幅度及强度大 于南方地区的河流:小集水面积的河流大于大集水面积的河流:植被较差的地区大于摧被较 好的地区:洪水季节大于中、枯水季节。 冲积平原河流的河床由大量的疏松沉积物即泥沙构成,这些疏松沉积物在不同条件水流 的作用下,或冲刷,或继续沉积,或者基本平衡:山区河流的河床尽管由基岩组成,但在水 流常年累月的侵蚀作用下,也发生者相应而缓慢的变化。 河道水流与河床相互依存,相互制约,相互促使变化发展。因此,其不恒定性也是相互 联系的。一方面,来水来沙情况的不恒定性,不可避免地要引起河床时而剧烈、时而和缓的 变化:另一方面,河床的冲淤变化也必然改变河道水流。例如河床的冲淤改变水流的含沙量, 流速的分布、大小等。 4.河道水流的非均匀性 涉及运动的各物理量沿流程不变的水流为均匀流,达到均匀流的条件是水流为恒定流 水流边界是与流向平行的棱柱体。河道水流的非恒定性包括了来水来沙的不恒定性和边界的 不恒定性,因此河道水流为严格意义上的非均匀流。 在解决实际问题过程中,对于比较顺直的河段,如果来水米沙情况基本稳定,河床基本 处于不冲淤的相对平衡情况,过水断面及流速沿程变化不大,水面坡度、床面坡度及能坡基 本平直而相互平行,就可以当做均匀流处理。 二、河道水流中的阻力 重力、惯性力与阻力为水流中最重要的力。与清水水流相比,河道水流中的力要复杂得 多,其所起的作用,也是很不相同的。例如清水水流的重力起着克服阻力的作用:而在河道 水流中,重力来自液相的水和周相的泥沙,有克服阻力、促使运动的一面:也有抵抗运动的 一面。 研究河道水流阻力损失的目的当然主要在于确定河道的泄流能力和输沙能力。对于具有 ·定过水新面和比降的河道,水流的流速有多大,不仅决定能通过多大流量,而且直接与泥

沙运动的强度有关,因此研究水流阻力损失一直是河流动力学的基本问题 阻力问题,本来就是普通水力学中性质复杂,影响广泛而又解决得不够妥善的一个问题 在河道水流中,这一问题更加复杂。因此,除在这里介绍外,在以后的相关章节里,还将讨 论这一问题。 1,明渠二维水流的阻力损失 这里我们首先回倾一下最简单情形的由明渠表面粗糙引起的二维恒定均匀流的阻力问 题。 水力学中一般用阻力系数元、糙率系数和谢才系数C表示水流阻力,其中阻力系数 为无量纲数,糙率系数n和谢才系数C是有量纲的经验系数。 1775年谢才(A.Chey)提出了明渠二维均匀流平均流速计算公式 U-CRJ I888年达西-魏斯巴赫(Darey-Weisbach)提出如下公式 4R 2g 1890年出现了至今仍在广泛使用的曼宁公式 U-IRiyn 式中,U为时均流速:R为水力半径;J为比降:g为重力加速度 对比上面公式不难发现,糙率系数与谢才系数之间有如下关系 C=IRIG n 谢才系数和阻力系数之间的关系是 c-图 上述公式中,曼宁公式与谢才公式完全属于经验公式,甚至连系数都不得不带有量纲。 但对于比较简单情形的二维均匀流来说,只要在积累较多的经验和资料的基础上,合理准确 地选择糙率系数,那么这两个公式可以满足要求。 2.河道水流阻力损失 在水力学、流体力学中我们知道,水流阻力损失可以概括为两部分,即克服流层间粘滞 性剪切力的阻力损失和克服紊动剪动力的阻力损失。当水流的雷诺数很大,水流已经进入阻 力平方区时,可以只考虑奈动剪动力。因此一般管道或明槽水流的阻力损失与河道水流阻力 损失的差异主要来源于二者紊动的差异。 与水力学中顺直管道和棱柱体明槽水流中发生的紊动相比,河道水流的素动在紊动尺 度、紊源上要复杂得多。前者主要是粗糙边壁附近小尺度的紊动,由大、中、小尺度构成的

紊动结构虽不能完全挂除,但不占主导地位:而对后者,根据张瑞瑾的研究,素源除了普 通意义的相糙边壁外,还包括河势、河相、成型淤积体、河底或河岸的大凸大凹、沙纹及沙 波等,这些奈源的尺度是边壁粗糙完全不能比拟的。大尺度的紊源产生大尺度的紊动,大尺 度紊动尺度大,发生的周期比较清楚,与四周水流具有一定的相对速度,一次掺混可以达到 较大的距离(与河道各种特征几何尺度同数量级),在掺混过程中发生质量扩散、动量扩散 及动能扩散,涡体逐渐变小,并逐渐减弱原有的周期性与力学规律性,而随机性和各向同性 逐渐加大。这就是说,凡具有大尺度素动的水流必然同时具有中,小尺度的素动:而具有小 尺度素动的水流却可以不同时具备大、中尺度素动。素动就能的传递米说, 般是单向的 即由大尺度紊动传递给中尺度紊动,再传递到小尺度紊动,或直接由大尺度素动传递到小尺 度紊动,最后随小尺度紊动而转化为热能而散失。要继续维持这一具有大、中、小尺度素动 结构的持续存在的水流图形,必须经常提供一定的有效能量,通过水流的紊动能,最后转化 为热能而消散 因此对于河道水流,“糙率系数”的内含应该是极为复杂的。作为属于阻力平方区的 时均流速U的表达式中代表水流阻力效果的综合因素,它当然直接与水流中的紊源和紊动 结构有关,与大至河势,小至河床床沙粒径有关。 在一般管流及明槽流中,糙率系数的复杂性随着研究的深入而逐步为有关的科技工作 者所理解,因而出现以爱因斯坦、罗佐夫斯基等为首的提出将综合性的糙率系数先进行分 解,再采用叠加的补救方法巴,这种方法在解决某些实际问题中,如河底与河岸的不同粗糙 度对河道水流的影响问题等,可以取得有关河道水流阻力损失、流速分布等方面某些粗略成 果,在更合理的办法出现以前,为了应付当前的一些问恶,这种粗略的办法还未完全失去存 在的价值。 第三节河道水流的运动结构 一、河道水流的流型、主副流及流速分布 1.河道水流的流型 在水力学中将流体运动区别为紊流和层流两大类型,在紊流中又分为光滑区、粗糙区(或 阻力平方区),以及介于二者之间的两个过渡区。 河道水流普遍具有较大的雷诺数。拿一条水力半径R的数量级为10'cm、流速U的数 量级为10cms、摩阻流速u.的数量级为1.6X10cms、运动粘滞性系数v的数量级为 10m5的小小河流大致估算一下,它的诺数Re=Re-R将达到10,即它的雷诺 数已经完全进入阻力平方区。 当然,不能进入阻力平方区的河道水流也不是完全没有,但从工程观点看问题应该得出 的结论是:河道水流的雷诺数一般都比较大,其流型一般居于阻力平方区。 9

2.河道水流的主流与副流 主流(又称正流、元生流)是水流沿着河槽总方向的流动。它一般是在重力作用下产生 的。在流动过程中,水流的流线基本上是相互平行的,水流的速度向量也是互相平行的,而 且都平行于河槽的轴线。 在河道水流中,与主流相对应的有副流(又称次生流)。副流与主流不同,不是由河床 纵比降的总趋势决定的,而是由于纵比降以外的其它因素所促成的。副流实际是在水流内部 产生的一种大规模的水流旋转运动。它可以因重力作用而引起,也可在其它的力(内力或外 力)作用下产生。在副流中,有的具有复归性,或者基本上与主流脱离,在一个区域内呈循 环式的封闭流动:或者与主流或其它副流结合在一起,呈螺旋式的非封闭的复归性流动。具 有复归性的次生流,我们称之为环流四。主流一般以纵向为主,环流则不然,它因产生的原 因不同,具有不同的轴向,因此输沙的方向也不限于纵向。可以说,河流中的横向输沙主要 是靠有关的环流造成的,而不是靠主流或纵向水流造成的。因此,一个河段的冲淤动态,除 了受主流的影响之外,还受环流的重要影响。如果只看到纵向水流的作用,而忽视环流的作 用,则要对河段冲淤动态全面了解,在很多情况下是不可能的。 应该注意的是,副流与水流中的紊动漩涡是有所不同的。紊动漩涡一般尺度较小,并且 常常是没有规则的。而副流一般规模都较大,而且它们的位置和影响范围都是比较固定的, 3.河道水流的流速分布 在水力学中,我们学习了二维恒定均匀流的流速分布,包括层流及紊流两种流态。前面 已经指出,几乎所有的天然河道水流都具有三维性、不恒定性、不均匀性,其流速分布显然 不能直接应用水力学所掌握的流速分布公式来描述。 但是天然河道的情况也是千差万别,有的冲积平原河流非常宽浅,水深沿河宽的变化虽 然也比较大,但与其横向的几何尺度相比,这种变化就比较小了,这种情况下,河道水流更 多地表现出接近二维,尤其是水流流速分布方面。在这种情况下,可以近似使用二维均匀流 的流速分布公式来描述河道水流的流速分布。实际上,在现阶段的河流动力学,还难以提出 符合实际的三维流速分布公式,人们通常用经验的方法研究河道水流的流速分布。 (1)几个常用的二维水流流速分布公式 1)卡门-普兰持(Th.von..Kama-L.Prandtl)对数流速分布公式间 Uas-n (1-7) H. 式中,“、“及分别为水面处最大流速、位于相对水深号处的时均流速及摩阻流速 (4,=√gh):h为水深:g为重力加速度:J为能坡:k为卡门通用常数,在清水水流中 k=0.4:1为掺混长。 2)指数流速分布公式:指数形式的流速分布公式,结构简单,出现得较早。但在卡门一 普兰特对数流速分布公式问世后,前者逐渐为后者所代替。1984年,陈永宽又对指数流速