
二、数据处理的一般方法 数据处理是为求被测量最接近真值的估计值,并作可信程度评定 1、系统误差的消除 ①找出规律--修正值 ②测量方法--避免出现系统误差 2、粗大误差的减少办法和剔除 显然与事实不符-歪曲测量结果-主观避免--剔除(发现) 3、随机误差的分析处理-统计方法 1)分布:正态分布(高斯分布)--大多数; 均匀分布-量化误差、舍入误差; 其它--正弦分布、二次分布、卡方分布、指数分布等 2)主要特征量: 数学期望(Expectation)4--随机变量的总体期望u就是其真值xo 标准偏差(Standard deviation)o--测量精密度的标志
1、系统误差的消除 ② 测量方法 --- 避免出现系统误差 数据处理 是为求被测量最接近真值的估计值 ,并作可信程度评定 ① 找出规律 --- 修正值 二、数据处理的一般方法 2、粗大误差的减少办法和剔除 显然与事实不符 --- 歪曲测量结果 --- 主观避免 --- 剔除(发现) 3、随机误差的分析处理--- 统计方法 正态分布(高斯分布) --- 大多数; 其它 --- 正弦分布、二次分布、卡方分布、指数分布等 1)分布: 均匀分布 --- 量化误差、舍入误差; 数学期望(Expectation ) --- 随机变量的总体期望 就是其真值x0 标准偏差(Standard deviation) --- 测量精密度的标志 2)主要特征量:
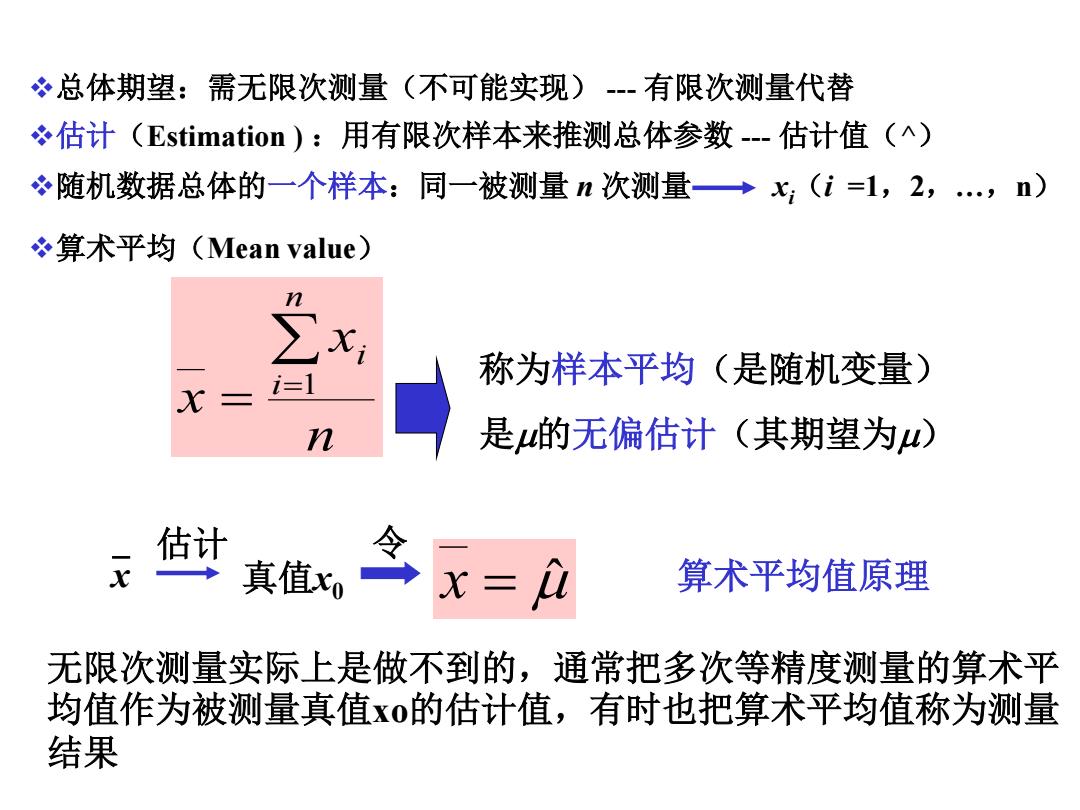
·总体期望:需无限次测量(不可能实现)--有限次测量代替 估计(Estimation):用有限次样本来推测总体参数-估计值(^) 随机数据总体的一个样本:同一被测量n次测量→x:(i=1,2, ...n) 冬算术平均(Mean value) ∑ Xi i=1 称为样本平均(是随机变量) X n 是的无偏估计(其期望为4) 估计 真值x x= 算术平均值原理 无限次测量实标上是做不到的,通常把多次等精度测量的算术平 均值作为被测量真值x0的估计值,有时也把算术平均值称为测量 结果
x 真值x0 估计 x ˆ 算术平均(Mean value) n x x n i i 1 称为样本平均(是随机变量) 是的无偏估计(其期望为) 总体期望:需无限次测量(不可能实现) --- 有限次测量代替 估计(Estimation ) :用有限次样本来推测总体参数 --- 估计值(^) 随机数据总体的一个样本:同一被测量 n 次测量 xi(i =1,2,…,n) 令 算术平均值原理 无限次测量实际上是做不到的,通常把多次等精度测量的算术平 均值作为被测量真值xo的估计值,有时也把算术平均值称为测量 结果

算术平均值原理 B:=X;-X0 随机误差(无系统误差) ∑e, ∑(x,-x) ∑x i=1 i=1 -X0=灭-X0 n n n lim之e,=0 随机误差的抵偿性 n→o∞ i=1 ∴.limc-xo=u-xo=0 1→o0 ∴.u=X0 令x=2
算术平均值原理 0 0 1 1 1 0 0 1 0 0 0 ( ) lim 0 lim 0 ˆ i i n n n i i i i i i n i n i n x x x x x x x x n n n x x x x x 令 随机误差的抵偿性 随机误差(无系统误差)