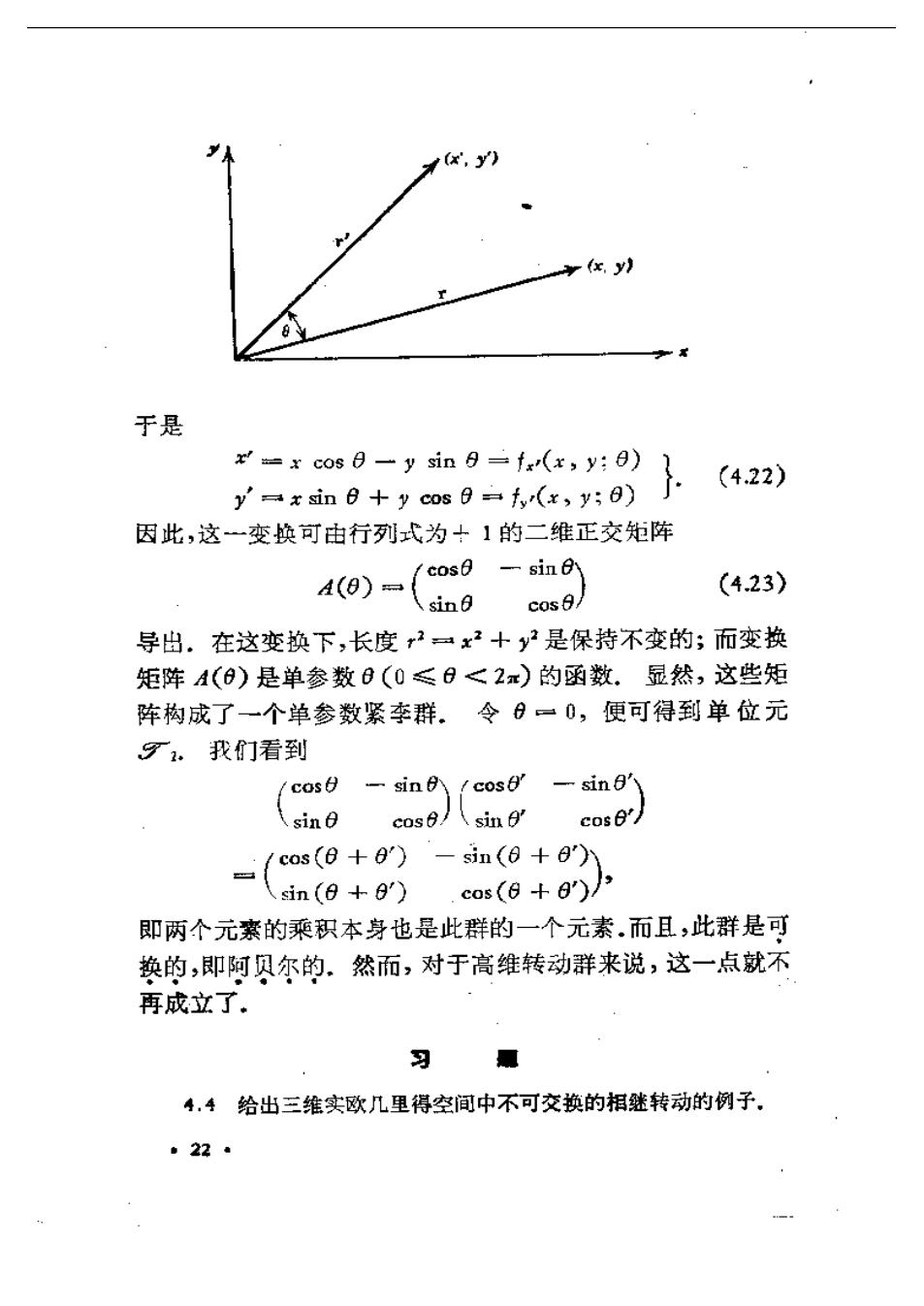
(x.y) (x.y) 于是 x=xcos日一ysin9=fx(x,y:θ) (4.22) y'=x sin 8+y cos(x,y;) 因此,这一变换可由行列式为十1的二维正交矩阵 4o-(mgg9 (4.23) cos9/ 导出.在这变换下,长度2一x2+y2是保持不变的;而变换 矩阵A(0)是单参数0(0≤日<2x)的函数.显然,这些矩 阵构成了一个单参数紧李群.令6一0,便可得到单位元 。我们看到 (coso -sincos-sin' sin0 cos6 sin 0'cose' -(os(8+9-n(0+6r sin(0+g) .cas(6+8') 即两个元素的乘积本身也是此群的一个元素.而且,此群是可 换的,即阿贝尔的。然而,对于高维转动群来说,这一点就不 再成立了。 习 4,4给出三维实欧几里得空间中不可交换的相继转动的例子」 ·22·

4.6无穷小转动 现在,我们研究无穷小变换的作用。无穷小转动是坐标 的一种正交变换;在这种变换下,一个向量变换前的分量与变 换后的分量几乎一样,即它们只差一个无穷小量.因此,对于 维向量r来说,它的第i个分最x差不多跟x,是一样的: 口++…+8n,回4+∑,(4,24》 这里8,是无穷小量.例如,在S0(2)中,我们有 x'=x一y89 y'=x80+y (因为当日→0时,c0s8+1,s知6→69).(4,24)式可以重 新写成 “会a+ (4.25) 但是,6,就是单位矩阵9;因此,应用矩阵符号,我们就有 x-(9+8)x. (4.26) 这里,8是由无穷小量构成的一个矩阵,而今是单位矩阵 4.7一般变换 现在我们来考虑一般的变换T。,它把维空间中的一个 点x=(x1,…,)变换城另一个点x题(xi,…,x).设 变换T。由下列”个参数标定 a(a1,…,a,). 这样 X'=xT.=f(x:a). (4.27) 取另一个变换 x”mx'T=(x';b) (4.28) ·23

我们假定这些变换都是准一的,即有一个而且只有一个变换 能把x变换为x’, 显然,如果我们记 X'=xT 那么 x”=xTb=xT.Tb=gTe (4.29) 这里 c=p"(a,b)(p=1,·,r).(4.30) 或者,为了简洁起见,写成c一p(a,b).例如,在S0(2)中 就有 x'=xTo=f(x,y;8), x”ex'Ta=f(x',y';) =xToToxTo+e=f(x,yi0+8). 由(4.29)和(4.30)式得到 XT.Tb -XTgin,b) 以及 ff (x:a);bl=f[x;o(a,b)]. 其中的印(a,b),假定是到任意阶的连续可微函数。 如果变换T。构成一个群,那么函数P必须满足下列条 件: 1.必定有一个单位元T。存在,使得 &=P(a,8)=p(a0,a). 如果我们把a,取作原点,则有a=0,因此 a=p(a,0)-p(0,a). (4.31) 2.存在着逆变换T。1口T,使得 T,T。=T.T.2=② p'(&',a)=p"(a,a')=0. (4.32) 3,满足乘法的结合律,即 ·29

T.(TT)=(T.TL)T.. 这意昧着 Ia:(b,c)]-olo(a,b),cJ.(4.33) 这样,我们就有了(4.31),(4.32)和(4.33)这三个式子.(4.30) 中的函数甲(a,b)必须满足这些式子 48李群的无穷小算子 首先,讨论对一个变量作用的单参数群的简单情况.对 起始点 *o=f(xo;0) g+da 进行变换 x=f(x0;a), (4.34) 可到达x点;而进行变换 x+dxaK;a十da): (4.35) 则可以到达x十d:这一点.然而,我们可先到x,然后再通 过一个参数的无穷小改变6a,使得 x+dx=f(x;8a), 同样也能到达x+dx这一点。将上远结果展开有 d-(82)ua (4.36) 首先注意到 a+da=p(a,a), ·25·

因此 da-(0o(a,6 )6a=V(a)6a. (4.37) 、0b/b网 这样就建立了da与8a二者之间的联系. 现在来考港?个参数和个变量的一般情形.类似于 (4.36)式,我们有 -2rg)6的a=1,…,i-1…月 /a 或 dxi mm Ui(x)6a°, (4.38) 这里 x-(tg2). (4.39) 0a° 类似宁(4.37)式,简单地有 ar-(@geb2)sr, 86p 或 da"=Vg(a)6a°. (4.40) 这里 g@)(pg2X (4.41) 把:的逆记作,即:一δ.因此,由(4.40)式所产生 的变换的逆是 Baf (a)da, (4.42) 把(4.42)式代人(4.38)式中去,我们有 dx=U(x)g(a)da°, 或 0x=U(x):(a). (4.43) 0a°