南京大学：《计算机问题求解》课程教学资源（课件讲稿）离散概率基础

容斥原理 EF E1 2 1 E EnF EFG 2 1 EG FG G P(E U F) P(E UFUG)= =P(E)P(F)-P(E n F) P(E)+P(F)+P(G) -P(E n F)-P(E n G)-P(F n G) +P(E n FOG

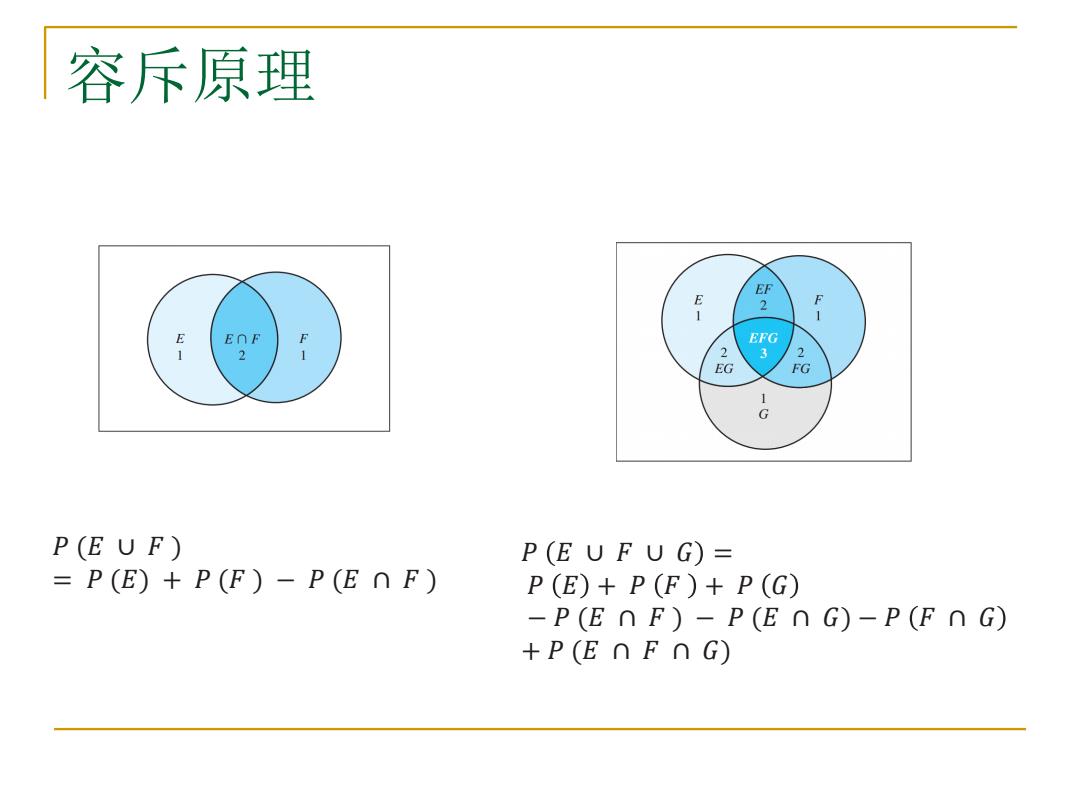
容斥原理 𝑃 (𝐸 ∪ 𝐹 ) = 𝑃 (𝐸) + 𝑃 (𝐹 ) − 𝑃 (𝐸 ∩ 𝐹 ) 𝑃 𝐸 ∪ 𝐹 ∪ 𝐺 = 𝑃 𝐸 + 𝑃 𝐹 + 𝑃 𝐺 − 𝑃 (𝐸 ∩ 𝐹 ) − 𝑃 (𝐸 ∩ 𝐺) − 𝑃 𝐹 ∩ 𝐺 + 𝑃 (𝐸 ∩ 𝐹 ∩ 𝐺)

容斥定律： 包含在若干个子集的并集中的元素个数： N(AUA2U.UAn)=S1-S2+S3-.+(-1)k+1Sk+.+(-1)m+1Sn where,Sx=>1Ai,Ai..A k =1,2.....n 1si1≤i2≤.≤ik≤n For an example:the formula for 4 subsets N-(IAl+JA2l+IA3l+IA4) +(IA∩A2l+lA1∩A2l+lA∩A4+|A2Ag|+lA2∩A4+lA3∩A4lI) -(IA1∩A2AgI+1A1A2∩A4l+|A∩A3∩A4+lA2nA3A4I) +IA∩A2A3∩A4l

容斥定律:                       1 i i ... i n k i i i n n 1 k k 1 1 2 n 1 2 3 1 2 k 1 2 k where S | A A ... A | k 1,2,..., n N(A A ... A ) S S S ... ( 1) S ... ( 1) S ，    For an example：the formula for 4 subsets N - (|A1 |+ |A2 |+ |A3 |+ |A4 |) + (|A1A2 |+|A1A2 |+|A1A4 |+|A2A3 |+|A2A4 |+|A3A4 |) - (|A1A2A3 |+|A1A2A4 |+|A1A3A4 |+|A2A3A4 |) + |A1A2A3A4 | 包含在若干个子集的并集中的元素个数:

容斥定律：否定形式 没有被包含在若干个子集的并集中的元素个数： N(AA,.A)=N-S1+S2-S3+.+(-1)Sk++(-1)”Sn where,,Sk=∑14∩A2∩.∩4|k=1,2,,n 1si1≤i2≤.≤ik≤n For an example:the formula for 4 subsets N-(IAl+JA2l+IA3l+IA4) +(IA∩A2l+lA1∩A2l+lA∩A4+|A2Ag|+lA2∩A4+lA3∩A4lI) -(IA1∩A2AgI+1A1A2∩A4l+|A∩A3∩A4+lA2nA3A4I) +lA∩A2∩A3∩A4l

容斥定律: 否定形式                      i i i n k i i i n n k k n k k S A A A k n N A A A N S S S S S 1 ... 1 2 1 2 3 1 2 1 2 where | ... | 1,2,..., ( ... ) ... ( 1) ... ( 1) ， For an example：the formula for 4 subsets N - (|A1 |+ |A2 |+ |A3 |+ |A4 |) + (|A1A2 |+|A1A2 |+|A1A4 |+|A2A3 |+|A2A4 |+|A3A4 |) - (|A1A2A3 |+|A1A2A4 |+|A1A3A4 |+|A2A3A4 |) + |A1A2A3A4 | 没有被包含在若干个子集的并集中的元素个数: