
3.自由度f(degreesoffreedom)在不引起旧相消失和新相形成的前提下,能够在一定范围内独立变动的强度性质称作系统的自由度即能确立系统状态的独立变量。如T,P,C例:①一杯水和一桶水:T,p,F2,状态相同,不用确定系统的大小;② NaCI(sln):T, p, c, f=3③ NaCI(饱和):T,p,f-2(浓度确定c=f(T))④H,0()-H,0(g)共存系统:f-1。因T,p中只有一个独立变量p=f(T)
3. 自由度f (degrees of freedom) 例: ①一杯水和一桶水: 在不引起旧相消失和新相形成的前提下,能够在一 定范围内独立变动的强度性质称作系统的自由度。 即能确立系统状态的独立变量。如T, p, c T, p, f=2,状态相同,不用确定系统的大小; T, p, c, f=3 T, p, f=2(浓度确定c=f (T)) f=1。因T, p中只有一个独立变量 p=f (T) 。 ② NaCl(sln): ③ NaCl(饱和): ④ H2O(l)-H2O(g)共存系统:
二、相律(phaserule)相律——联系K,Φ,f之间关系的规律:f-K-Φ+2相律的推导(Gibbs):设一相平衡系统:该系统有K个组分,Φ个相。在Tp恒定的条件下,有x如下表:β@α1xi(β)xi(@)xi(α)2x2(α)x2(β)x2(Φ)...···..kXk(β)Xk(@)Xk(α)
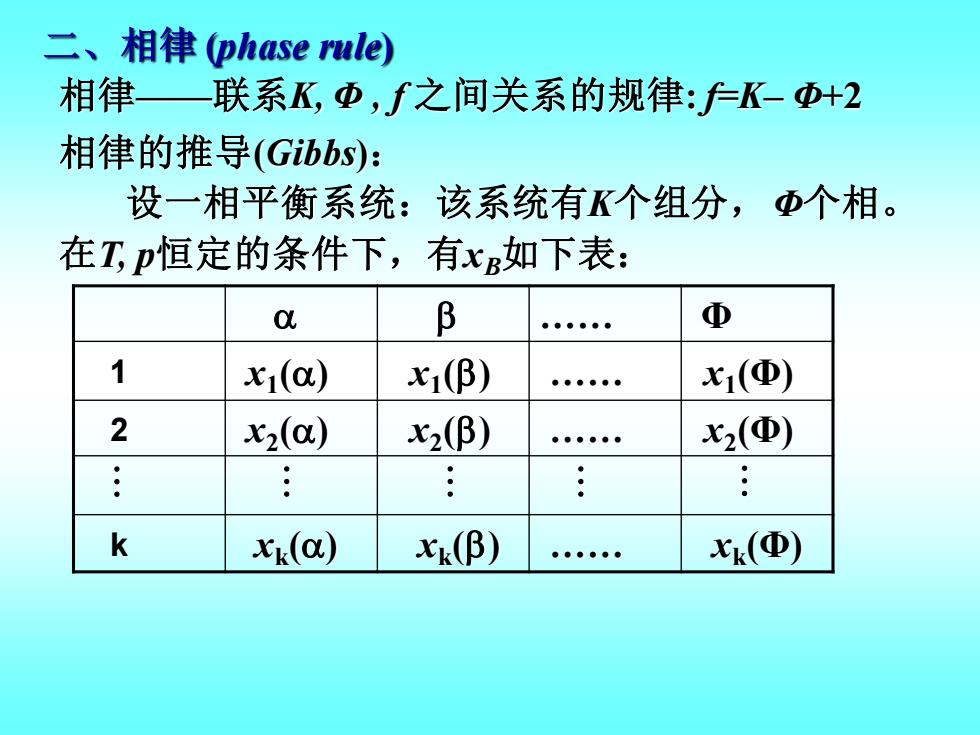
二、相律 (phase rule) 相律——联系K, Φ , f 之间关系的规律: f=K– Φ+2 . Φ 1 2 k 相律的推导(Gibbs): 设一相平衡系统:该系统有K个组分,Φ个相。 在T, p恒定的条件下,有xB如下表: x1 () x2 () xk () x1 () x2 () xk () . . . x1 (Φ) x2 (Φ) xk (Φ)

推导:该平衡系统有K个组分,Φ个相每一相中有(K-1)个浓度,共有Φ个相,除了T,p外还必须指定ΦK-1)个浓度根据相平衡条件,每个组分在各相中的化学势相等: u(α)= μ;(β)=.… u() 则每个组分有(Φ-1)个等式,K个组分则共有K(Φ-1)个等式。: f= Φ(K-1) + 2 -K(Φ-1)= K@-Φ + 2 - KΦ+Kf=K-Φ+2
推导:该平衡系统有K个组分, Φ个相 每一相中有(K–1)个浓度,共有Φ个相,除了T,p外 还必须指定Φ(K–1)个浓度。 f = Φ(K–1) + 2 f = K – Φ + 2 根据相平衡条件,每个组分在各相中的化学势相 等: i () = i () = . i (Φ) 则每个组分有(Φ–1) 个等式,K个组分则共有K(Φ–1)个等式。 – K(Φ–1) = KΦ–Φ + 2 – KΦ+K

注意:1)相律只适用于相平衡系统2)上面假设每个组分在每相中都存在,但这不是必要条件。因为在某一相中少一个组分,就会少一个平衡等式,相律公式不变2)f=K-Φ+2是一般关系,其中2是指T,p。若系统条件不符,则f-K-Φ+n。a.考虑更多的因素,如电场,磁场,n包括外界影响因素b.系统有多个T、p,n包括所有T、p则n=1或0。C.若系统指定温度或/和压力,!p146例题
注意: 1) 相律只适用于相平衡系统 2)上面假设每个组分在每相中都存在,但这不是必要条件。 因为在某一相中少一个组分,就会少一个平衡等式,相律 公式不变 2) f = K– Φ + 2是一般关系,其中2是指T, p。若系统条件不 符,则f=K – Φ +n。 a.考虑更多的因素,如电场,磁场.,n包括外界影响因素 b. 系统有多个T、p,n包括所有T、p; c.若系统指定温度或/和压力,则n=1或0。 p146 例题

例1Na,CO,有三种含水盐:Na,CO3:H,0, Na,C03:7H,0, Na,CO3:10H,0(1)pe下,与Na,CO3(aq)和冰共存的含水盐最多有几种?(2)30℃时,可与水蒸气共存的含水盐最多有几种?解:系统由Na,CO,和H,O构成,K-2若S=5,但存在三个平衡关系:R=3.Na,CO3+xH,O= Na,CO3xH,0:.K-2
例1 Na2CO3有三种含水盐: Na2CO3 H2O, Na2CO3 7H2O, Na2CO3 10H2O (1)py下,与Na2CO3 (aq)和冰共存的含水盐最多有几种? (2)30℃时,可与水蒸气共存的含水盐最多有几种? 解:系统由Na2CO3和H2O构成, K=2 若S=5, 但存在三个平衡关系: R=3, Na2CO3+xH2O = Na2CO3·xH2O K=2