
不精确的椭圆 概率上的椭圆还是模糊的椭圆?没有随机性的问题,所以 属于模糊问题。可否m,(x)=Prob{x∈A)?概率并不能包 括所有的问题。概率论是一种有限测量理论。 修
不精确的椭圆 概率上的椭圆还是模糊的椭圆?没有随机性的问题,所以 属于模糊问题。可否 ?概率并不能包 括所有的问题。概率论是一种有限测量理论。 ( ) Pr { } m x ob x A A =

二、模糊集合的几何图示:sets as points 将论域X的所有模糊子集的集合一模糊幂集合F(2)看成一 个超立方体I”=[0,]”,将一个模糊集合看成是立方体内 的一个点。非模糊集对应立方体的顶点。中点离各顶点等 距,最大模糊。 也是唯一满足以下特性的点:A=A⌒A=AUA=A (多值连续集合理论) mAnB=min(mA,mg)) muB=maX(m4,mg)) m=1-ma
二、模糊集合的几何图示:sets as points 将论域X的所有模糊子集的集合——模糊幂集合 看成一 个超立方体 ,将一个模糊集合看成是立方体内 的一个点。非模糊集对应立方体的顶点。中点离各顶点等 距,最大模糊。 也是唯一满足以下特性的点: (多值连续集合理论) (2 ) X F [0,1] n n I = c c c A A A A A A = = = min( , ) max( , ) c 1 A B A B A B A B A A m m m m m m m m = = = −
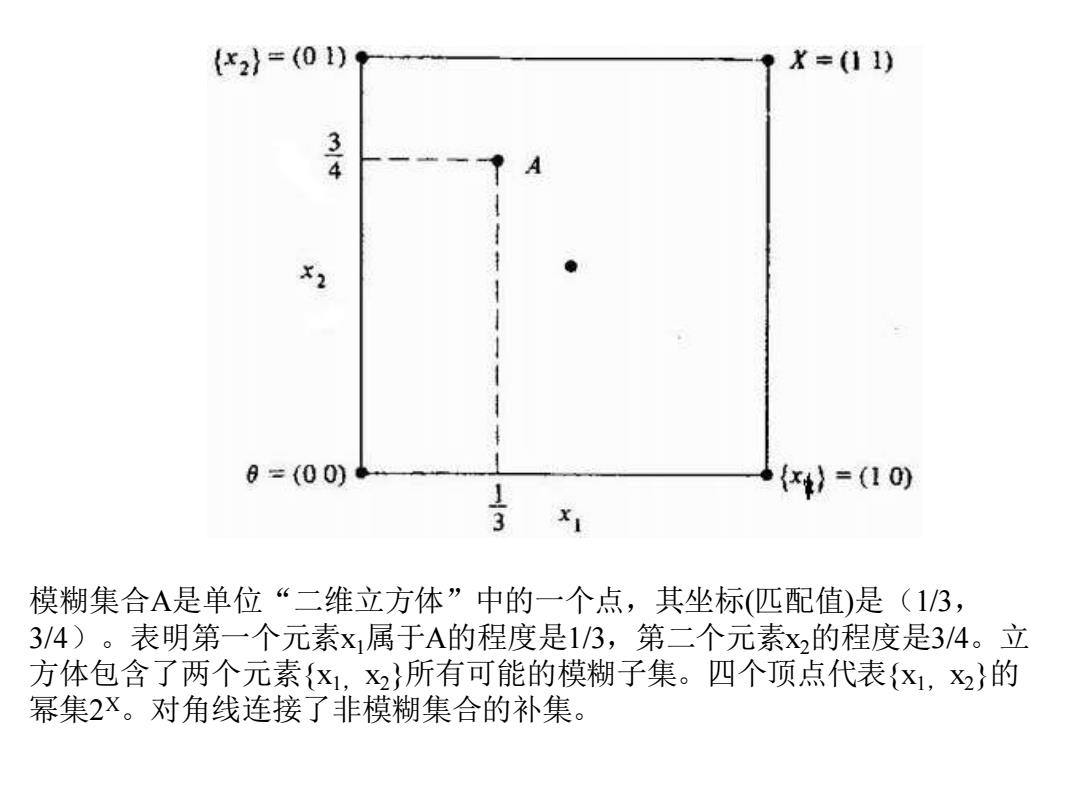
{x2}=(01) X=(11) A X2 ● 6=(00) {}=(10) 13 模糊集合A是单位“二维立方体”中的一个点,其坐标(匹配值)是(1/3, 3/4)。表明第一个元素x1属于A的程度是1/3,第二个元素x2的程度是3/4。立 方体包含了两个元素{x1,x2}所有可能的模糊子集。四个顶点代表{X1,X2}的 幂集2x。对角线连接了非模糊集合的补集
模糊集合A是单位“二维立方体”中的一个点,其坐标(匹配值)是(1/3, 3/4)。表明第一个元素x1属于A的程度是1/3,第二个元素x2的程度是3/4。立 方体包含了两个元素{x1,x2}所有可能的模糊子集。四个顶点代表{x1,x2}的 幂集2 X。对角线连接了非模糊集合的补集