边独立集(Edge Independent Set) ·边独立集(edge independent set)l 匹配 -A set of independent edges of G 0 极大边独立集(maximal edge independent set)极大匹配 一不是任何一个边独立集的真子集 ·最大边独立集(maximum edge independent set)最大匹配 -具有最大势(cardinality)的边独立集 0 边独立数(edge independence number)最大匹配的势 一最大边独立集的势 -a'(G) V, e e e N N ea 11
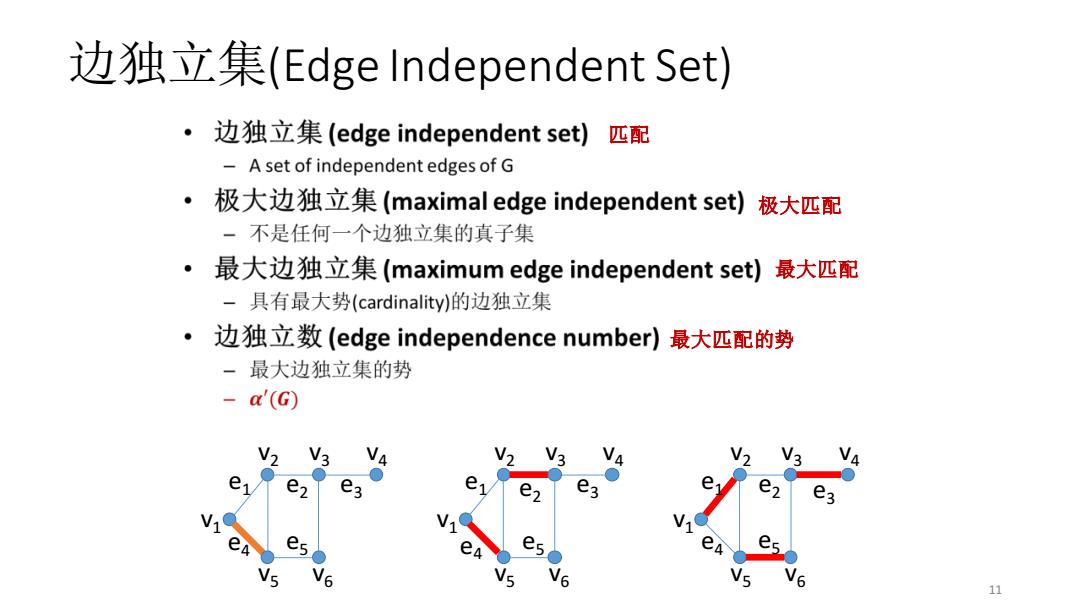
边独立集(Edge Independent Set) 11 v1 v2 v3 v4 v5 v6 e1 e4 e2 e3 e5 v1 v2 v3 v4 v5 v6 e1 e4 e2 e3 e5 v1 v2 v3 v4 v5 v6 e1 e4 e2 e3 e5 匹配 极大匹配 最大匹配 最大匹配的势
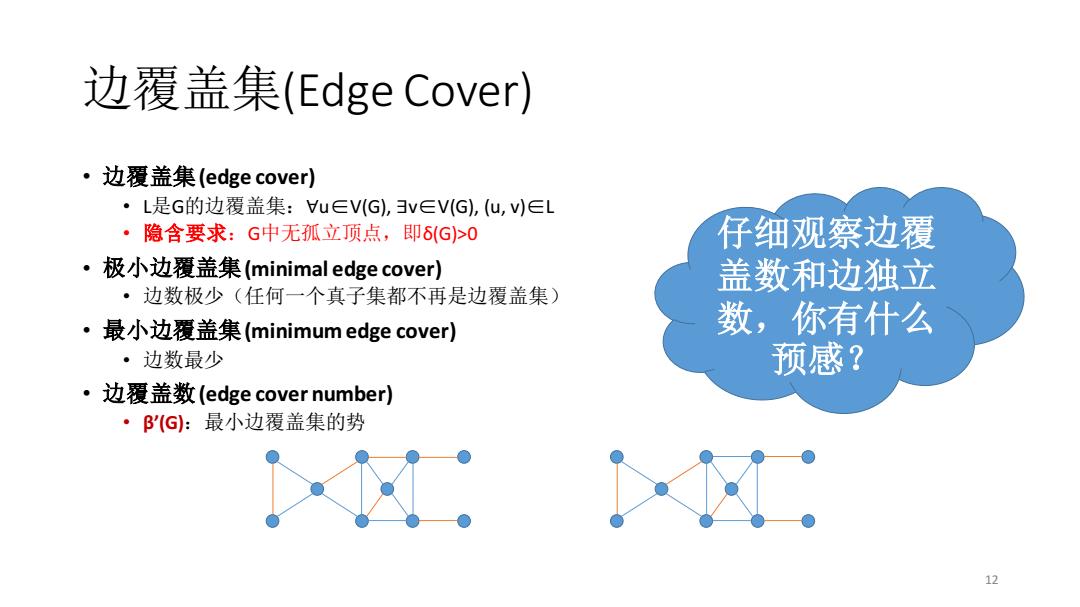
边覆盖集(Edge Cover) ·边覆盖集(edge cover) ·L是G的边覆盖集:u∈V(G),v∈V(G),(u,v)∈L ·隐含要求:G中无孤立顶点,即6(G>0 仔细观察边覆 ·极小边覆盖集(minimal edge cover) 盖数和边独立 ·边数极少(任何一个真子集都不再是边覆盖集) ·最小边覆盖集(minimum edge cover) 数,你有什么 ·边数最少 预感? ·边覆盖数(edge cover number) ·'(G:最小边覆盖集的势 12
边覆盖集(Edge Cover) • 边覆盖集(edge cover) • L是G的边覆盖集:∀u∈V(G), ∃v∈V(G), (u, v)∈L • 隐含要求:G中无孤立顶点,即δ(G)>0 • 极小边覆盖集(minimal edge cover) • 边数极少(任何一个真子集都不再是边覆盖集) • 最小边覆盖集(minimum edge cover) • 边数最少 • 边覆盖数(edge cover number) • β’(G):最小边覆盖集的势 12 仔细观察边覆 盖数和边独立 数,你有什么 预感?

边覆盖集与边独立集的关系 ·最大边独立集覆盖2α(G)个点,其余的点,谁去覆盖? 05 每个点,必须有一条边去覆盖: ·如果有一条边覆盖两个这样的点,这条边可以放入“最大边独立集” ·其余点可由n-2a'(G)条边覆盖 ·因此:β'(G)<=a(G)+n-2a(G)=n-a(G: >a(G)+β'(G)<=n
边覆盖集与边独立集的关系 • 最大边独立集覆盖2α’(G)个点,其余的点,谁去覆盖? • 每个点,必须有一条边去覆盖: • 如果有一条边覆盖两个这样的点,这条边可以放入“最大边独立集” • 其余点可由n-2α’(G)条边覆盖 • 因此:β’(G)<=α’(G)+(n-2α’(G))=n-α’(G): ➢α’(G)+β’(G)<=n