
二部图中最大匹配的存在性 Theorem 8.3 Let G be a bipartite graph with partite sets U and W such that r=Us W.Then G contains a matching of cardinality r if and only if G satisfies Hall's condition. 必要性: G B D F K L M
二部图中最大匹配的存在性 必要性:

Theorem 8.3 Let G be a bipartite graph with partite sets U and W such that r=U W.Then G contains a matching of cardinality r if and only if G satisfies Hall's condition. 你能想到用数学归纳 ·奠基:U川=1,显然 法证明吗? ·假设:U川<=|W|且1<=U川<k且满足Hall条件时均存在最大匹配 ·为什么这里需要采用“强”数学归纳法? ·归纳:当U<=W|以及U|=k且满足Hall条件时 ·1,如果对U的任意子集S,IN(S)川>IS引。 ·2,如果有U的某个真子集S,IN(S)川=|S。 ·分别构造上述两种情况下的最大匹配 请注意:为什么我们 要区分这两种情形?
• 奠基: |U|=1,显然 • 假设:|U|<=|W|且1<=|U|<k且满足Hall条件时均存在最大匹配 • 为什么这里需要采用“强”数学归纳法? • 归纳:当|U|<=|W|以及|U|=k且满足Hall条件时 • 1,如果对U的任意子集S,|N(S)|>|S|。 • 2,如果有U的某个真子集S,|N(S)|=|S|。 • 分别构造上述两种情况下的最大匹配 你能想到用数学归纳 法证明吗? 请注意:为什么我们 要区分这两种情形?
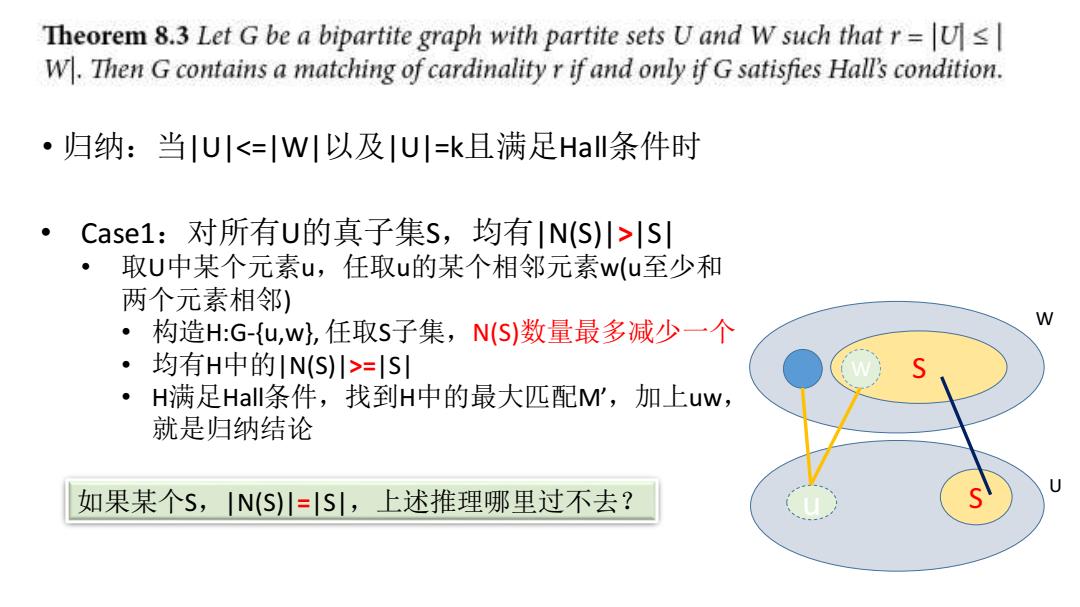
Theorem 8.3 Let G be a bipartite graph with partite sets U and W such that r=Us W.Then G contains a matching of cardinality r if and only if G satisfies Hall's condition. ·归纳:当U川<=WI以及U川=k且满足Hall条件时 case1:对所有U的真子集S,均有IN(s)川>lS ·取U中某个元素u,任取u的某个相邻元素w(u至少和 两个元素相邻) ·构造H:G-{u,w,任取S子集,N(S)数量最多减少一个 W ·均有H中的IN(S)川>=|S H满足Hal条件,找到H中的最大匹配M',加上uw, 就是归纳结论 如果某个S,N(S)川=S,上述推理哪里过不去?
U W S u S W • 归纳:当|U|<=|W|以及|U|=k且满足Hall条件时 • Case1:对所有U的真子集S,均有|N(S)|>|S| • 取U中某个元素u,任取u的某个相邻元素w(u至少和 两个元素相邻) • 构造H:G-{u,w}, 任取S子集,N(S)数量最多减少一个 • 均有H中的|N(S)|>=|S| • H满足Hall条件,找到H中的最大匹配M’,加上uw, 就是归纳结论 如果某个S,|N(S)|=|S|,上述推理哪里过不去?
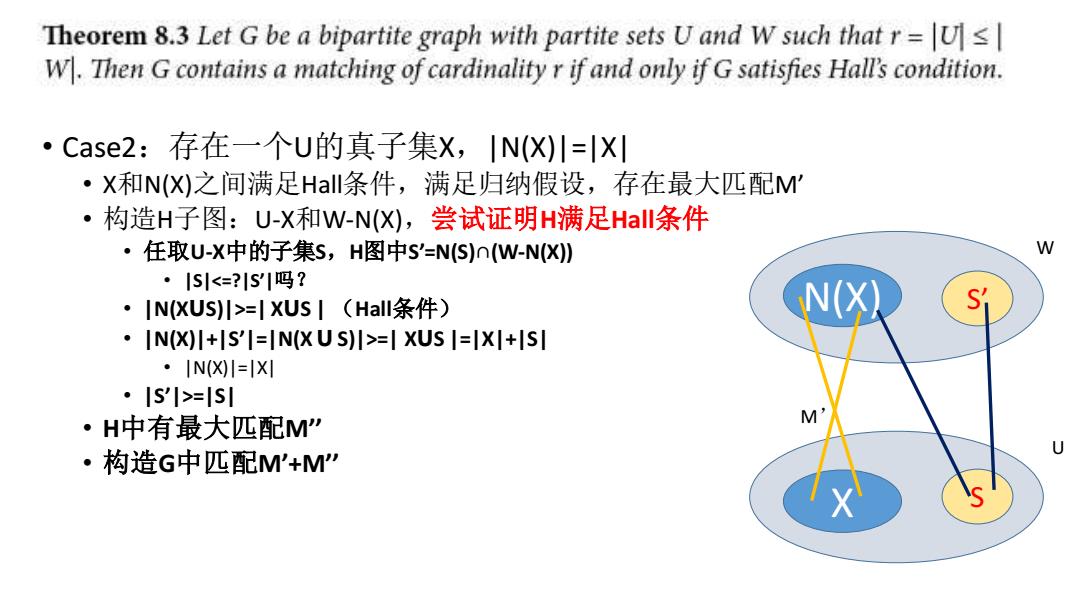
Theorem 8.3 Let G be a bipartite graph with partite sets U and W such that r=Us W.Then G contains a matching of cardinality r if and only if G satisfies Hall's condition. ·Case2:存在一个U的真子集X,IN(X)川=X ·X和N()之间满足Hal条件,满足归纳假设,存在最大匹配M' ·构造H子图:U-X和W-N(X),尝试证明H满足HaII条件 ·任取U-X中的子集s,H图中s'=NS)n(W-N(X) W ·1S1<=?1S1吗? ·IN(XUs)l>=|XUsI(Hall条件) N() Si .IN(X)I+S'I=IN(XUS)I>=I XUS I=IXI+ISI ·IN(X)=X ·IsI>=lsl ·H中有最大匹配M” U ·构造G中匹配M'+M
• Case2:存在一个U的真子集X,|N(X)|=|X| • X和N(X)之间满足Hall条件,满足归纳假设,存在最大匹配M’ • 构造H子图:U-X和W-N(X),尝试证明H满足Hall条件 • 任取U-X中的子集S,H图中S’=N(S)∩(W-N(X)) • |S|<=?|S’|吗? • |N(XꓴS)|>=| XꓴS | (Hall条件) • |N(X)|+|S’|=|N(X ꓴ S)|>=| XꓴS |=|X|+|S| • |N(X)|=|X| • |S’|>=|S| • H中有最大匹配M’’ • 构造G中匹配M’+M’’ U W X N(X) S S’ M’

这个定理的直观含义是什么? Theorem 8.4 A collection [SS2....S of nonempty finite sets has a system of distinct representatives if and only if for each integer k with 1 sks n,the union of any k of these sets contains at least k elements. For example,consider the sets SS2,.S,where Hal婚姻定理 S1={1,2,3}S2={2,4,6} S3={3,4,5} S4={1,4,7} S5={1,5,6}S6={3,6,7} S7={2,5,7} Then this collection of sets has a system of distinct representatives.In particular,1,2,..., 7(that is,iS for i=1,2,...,7)is a system of distinct representatives.On the other hand,the sets S1,2...where S1={1,3,5,6} S%={3,4} S3={4,5} S4={3,4,5} S5={1,2,4,6}S%={3,5}, do not have a system of distinct representatives asSS3,4,5 sodistinct representatives do not exist for the sets
这个定理的直观含义是什么? Hall 婚姻定理