
证明:必要性设X是一个正则空 间,U是x的任何一个开邻域,则U是 不包含x的闭集 图示 从而x和U分别有开邻域V和V使 得VOY=Φ,从而V二Y' 所以VcY=cU 继续
证明: 必要性 设X是一个正则空 间,U是 x 的任何一个开邻域,则 是 不包含 x 的闭集, 从而 x 和 分别有开邻域 和 使 得 ,从而 , 所以 . U U V V1 V V = 1 V V1 V V V U 1 1 − − = 图示 继续
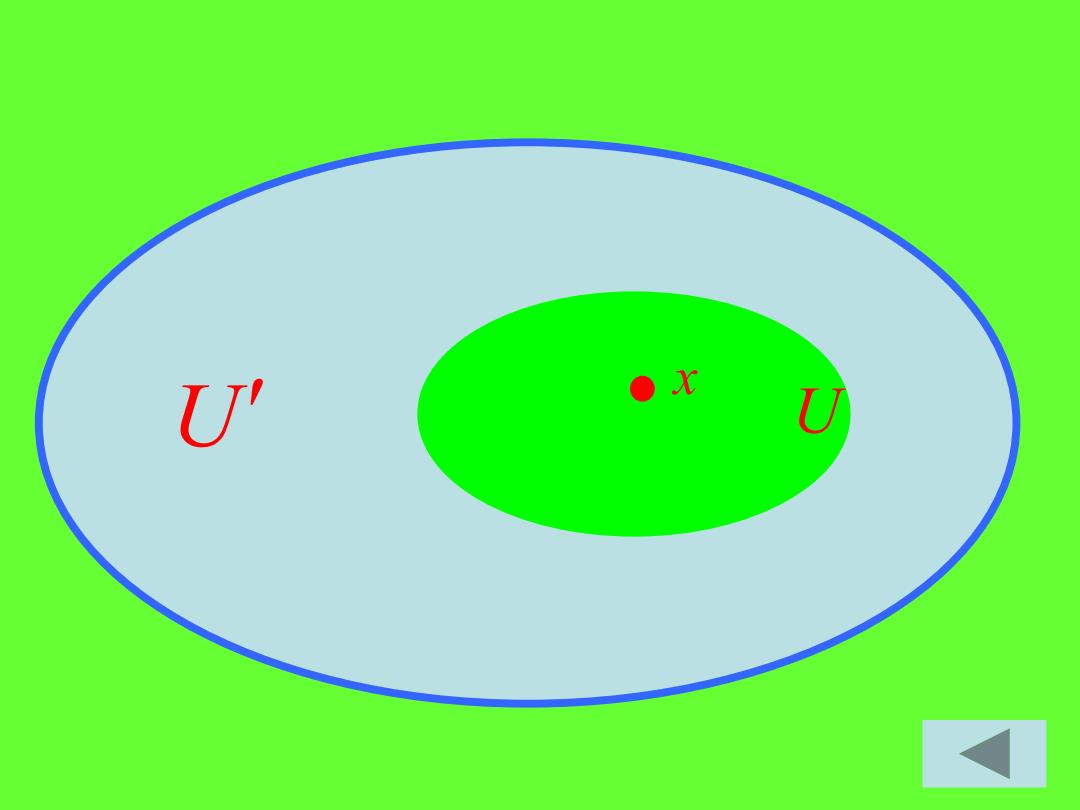
U' ●x U
x U U

充分性对任意的x∈X和不包含x 的任意闭集A,则A'是x的一个开邻域, 故有x的开邻域U使得UcA', 令 =乙- 则有AcY,所以V是A 的一个开邻域,并且有UOV= 这说明X是一个正则空间: 继续
充分性 对任意的x∈X和不包含x 的任意闭集A,则 是x的一个开邻域, 故有x的开邻域U 使得 , 令 ,则有 ,所以V是A 的一个开邻域,并且有 , 这说明X是一个正则空间. A U A ' V U − = A V U V = 图 继续
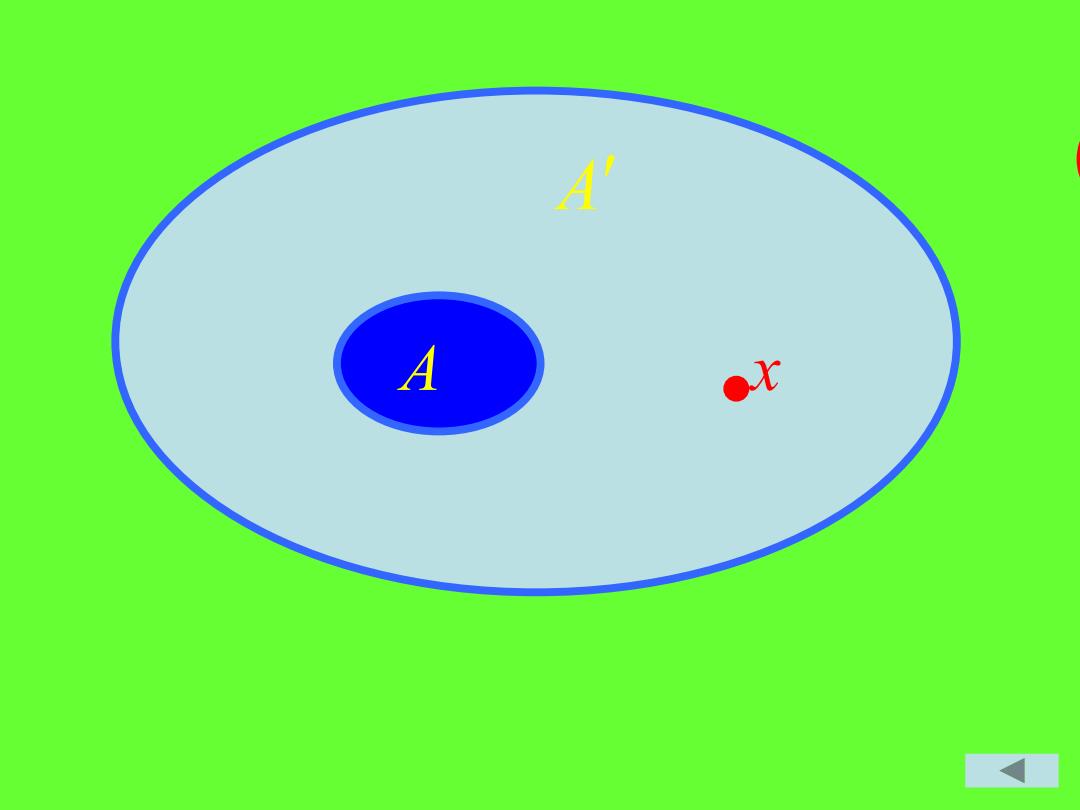
A A ●比
A x A