
§2一3溶脉的光散射挽象 本节要目 1 Tyndal1现象 2 Tyndall3现象的本质 3 Rayleigh公式 4超显微镜 5暗视野超聚光器 6粒子大小的推算 上页 下页 回主目录 返回 2024年9月5日
2024年9月5日 § 12-3 溶胶的光散射现象 本节要目
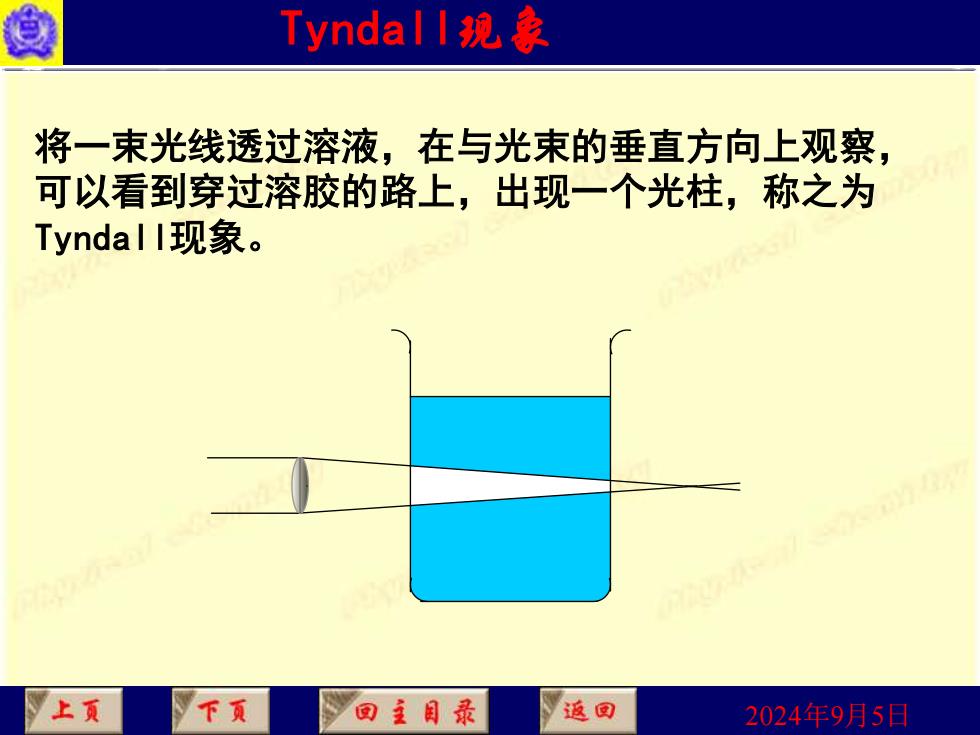
身 Tyndal l挽象 将一束光线透过溶液,在与光束的垂直方向上观察, 可以看到穿过溶胶的路上,出现一个光柱,称之为 Tyndal I现象。 上页 N下页 返回 2024年9月5日
2024年9月5日 Tyndall现象 将一束光线透过溶液,在与光束的垂直方向上观察, 可以看到穿过溶胶的路上,出现一个光柱,称之为 Tyndall现象

Tyndal I挽象的李质 可见光的波长约在400~700nm之间,当光线照射到分 散体系时,()若粒子直径大于入射光波长,则主要 发生光的反射;(2)若粒子直径大于入射光波长,光 波将环绕粒子而向四周发射与入射光频率相同的光,即 散射光(乳光)。由于溶胶粒子大小一般不超过100nm, 因此Tyndal川现象就是光的散射现象(乳光现象)。 虽然真溶液中分子或离子具有更小的直径,但散射光 的强度还与散射粒子的体积有关,故真溶液对光的散 射作用甚微。实际上,Tyndal l:现象已成为判别溶胶 与分子溶液的最简便的方法。 上页 回主目录 返回 2024年9月5日
2024年9月5日 Tyndall现象的本质 可见光的波长约在400~700 nm之间,当光线照射到分 散体系时,(1)若粒子直径大于入射光波长,则主要 发生光的反射;(2)若粒子直径大于入射光波长,光 波将环绕粒子而向四周发射与入射光频率相同的光,即 散射光(乳光)。由于溶胶粒子大小一般不超过100nm, 因此Tyndall现象就是光的散射现象(乳光现象)。 虽然真溶液中分子或离子具有更小的直径,但散射光 的强度还与散射粒子的体积有关,故真溶液对光的散 射作用甚微。实际上,Tyndall现象已成为判别溶胶 与分子溶液的最简便的方法

Ray leigh公式 Rayleigh研究了光的散射现象,得到了散射光强度I、 入射光波长入、入射光强度引、单位体积中的粒子数 v、粒子的体积0、分散相的折射率n1及分散介质的 折射率n2的关系式: 24π3vU2 I- 24 . 上页 下页 回主目录 返回 2024年9月5日
2024年9月5日 Rayleigh公式 Rayleigh研究了光的散射现象,得到了散射光强度I、 入射光波长、入射光强度I0、单位体积中的粒子数 、粒子的体积 、分散相的折射率n1及分散介质的 折射率n2的关系式: 0 2 2 2 2 1 2 2 2 1 4 3 2 2 24 I n n n n I + − =

Ray leigh公式 由此可见,散射光的强度: (1)随离子浓度的增加而增加; (2)随粒子体积的加大而显著增强; (3)入射光的波长愈短,散射光强度也就愈强; (4)分散相与分散介质的折射率相差越大,散射 作用越显著。 上页 下页 回主目录 返回 2024年9月5日
2024年9月5日 由此可见,散射光的强度: (1)随离子浓度的增加而增加; (2)随粒子体积的加大而显著增强; (3)入射光的波长愈短,散射光强度也就愈强; (4)分散相与分散介质的折射率相差越大,散射 作用越显著。 Rayleigh公式