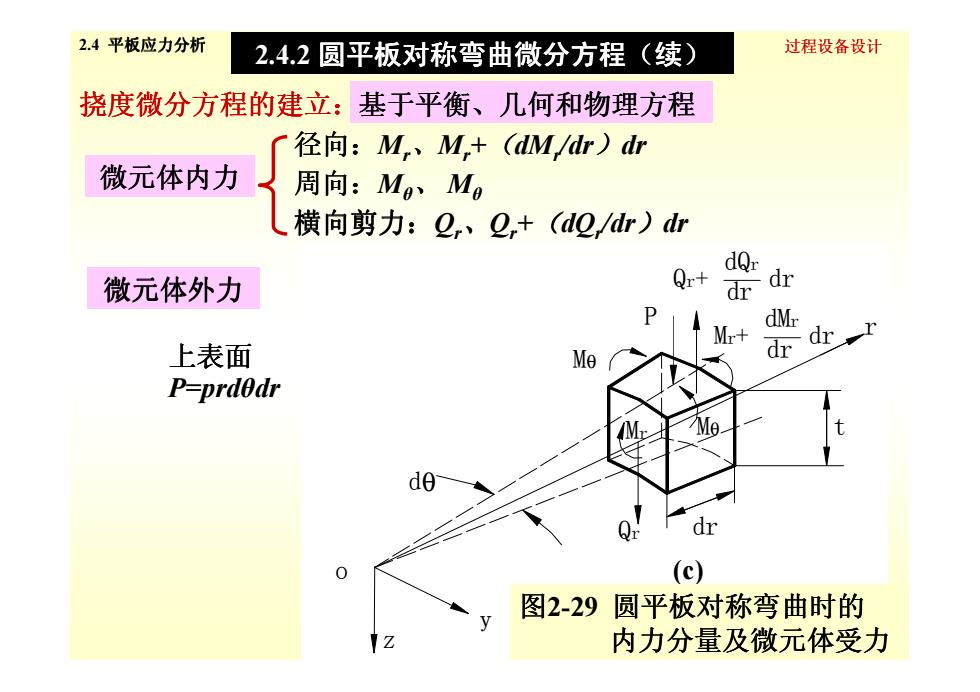
2.4平板应力分析 2.4.2圆平板对称弯曲微分方程(续) 过程设备设计 挠度微分方程的建立:基于平衡、几何和物理方程 径向:M、M+(dM/dr)dr 微元体内力 周向:Mg、Mg 横向剪力:2,、2,+(d0/dr)dr dQr 微元体外力 Qr+ dr dr dMr dr 上表面 Me dr P=prd0dr dr (c) 图2-29圆平板对称弯曲时的 内力分量及微元体受力
过程设备设计 挠度微分方程的建立:基于平衡、几何和物理方程 、几何和物理方程 微元体内力 径向:Mr、Mr+(dMr/dr)dr 周向:Mθ、 Mθ 横向剪力:Qr、Qr+(dQr/dr)dr 微元体外力 上表面 2.4 平板应力分析 2.4.2 圆平板对称弯曲微分方程 圆平板对称弯曲微分方程(续) r Qr+ P M dQr dr dr dr Mr+ dMr dr 12 上表面 P=prdθdr dθ z Qr dr t Mθ Mr Mθ P o c. dr Mr+ dr dQ y (c) 图2-29 圆平板对称弯曲时的 内力分量及微元体受力
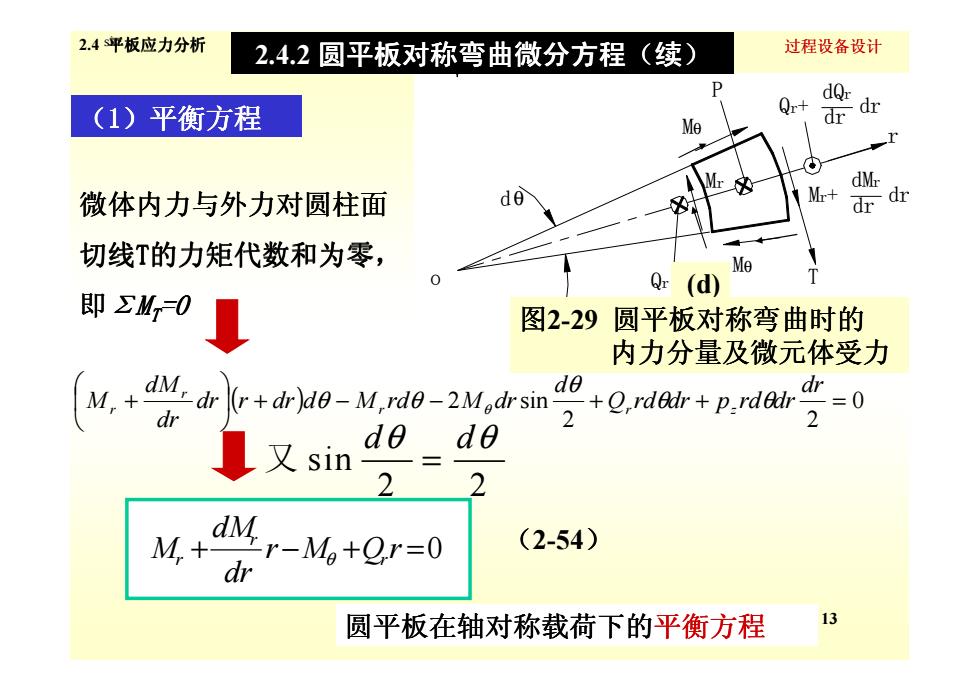
2.4平板应力分析 2.4.2圆平板对称弯曲微分方程(续) 过程设备设计 dQr (1)平衡方程 Qr+ Me dr dr dMr 微体内力与外力对圆柱面 de Mr+ dr dr 切线T的力矩代数和为零, Me Q (d) 即∑MO 图2-29圆平板对称弯曲时的 内力分量及微元体受力 、de dr dM dr (rdrde-M rd-2M,drsin +.rdeirtp,rdair=0 M,+ dr 又sin do do 2- 2 M.+ dM r-Mo+Qr=0 (2-54) dr 圆平板在轴对称载荷下的平衡方程 13
过程设备设计 (1)平衡方程 微体内力与外力对圆柱面 切线T的力矩代数和为零 T的力矩代数和为零, 即ΣMT=0 z dθ P T Mθ Mθ o Qr r d. Mr dMr Mr+ dr dr dr Qr+ dQr dr 2.4 平板应力分析 2.4.2 圆平板对称弯曲微分方程 圆平板对称弯曲微分方程(续) sin (d) 图2-29 圆平板对称弯曲时的 内力分量及微元体受力 13 ( ) 0 2 2 + − − 2 sin + + = + dr Q rd dr p rd dr d dr r dr d M rd M dr dr dM M r r z r r θ θ θ θ θ θ + r −M +Q r =0 dr dM M r r r θ (2-54) 圆平板在轴对称载荷下的平衡方程 sin 2 2 d d θ θ 又 = 内力分量及微元体受力
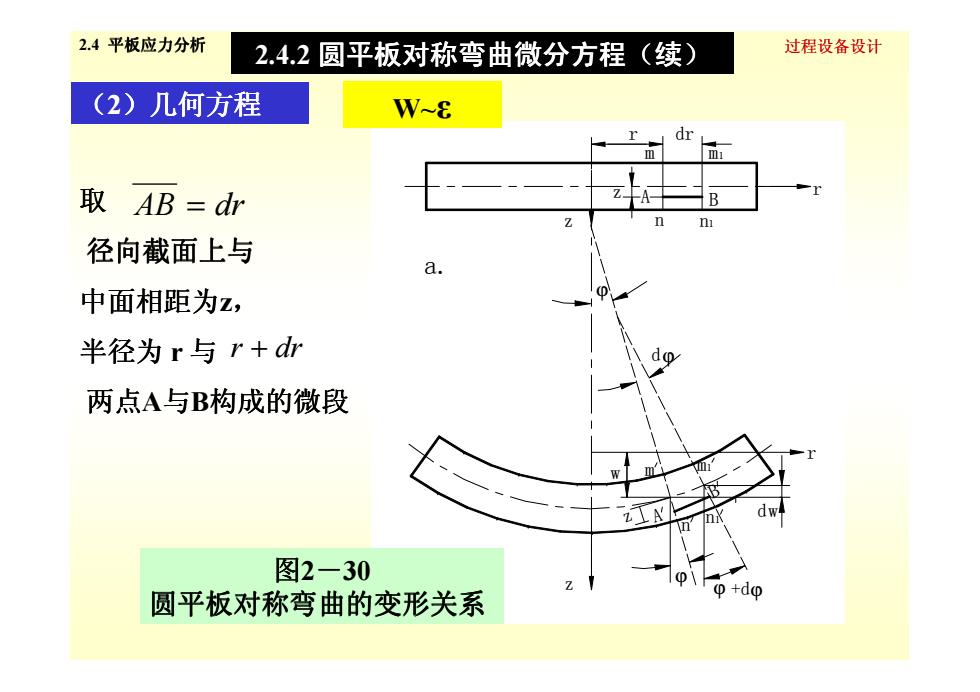
2.4平板应力分析 2.4.2圆平板对称弯曲微分方程(续) 过程设备设计 (2)几何方程 W-8 取AB=dr 径向截面上与 a. 中面相距为z, 半径为r与r+dr d o 两点A与B构成的微段 图2-30 圆平板对称弯曲的变形关系 0+d0
dϕ ϕ r dr r n n1 z A B m m1 z a. 过程设备设计 (2)几何方程 取 径向截面上与 中面相距为z, 半径为 r 与 r + dr AB = dr W~ε 2.4 平板应力分析 2.4.2 圆平板对称弯曲微分方程 圆平板对称弯曲微分方程(续) 14 dϕ +dϕ d ϕ n A n1 B ϕ z z m m1 b. r w w 半径为 r 与 两点A与B构成的微段 r + dr 图2-30 圆平板对称弯曲的变形关系